Рекуррентный метод наименьших квадратов
Рассмотренный нами метод наименьших квадратов требует для своей реализации хранения большого объема данных и не применим в реальных условиях, когда необходимо принимать решение на основе поступающей информации. В этом случае применяют рекуррентную форму метода наименьших квадратов.
Рассмотрим систему
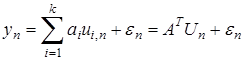 (1)
(1)
Как уже отмечалось, уравнение (1) может описывать широкий класс процессов и систем.
Путь для получения оценок используется текущее множество 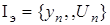 .
.
Полученная выше МНК-оценка вектора 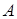 имеет вид
имеет вид
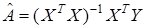 , (2)
, (2)
где
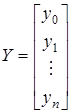 ,
, 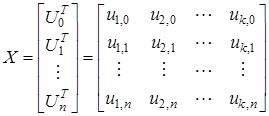 ,
,
и заданы на временном интервале 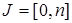 .
.
Преобразуем (2) так, чтобы получать оценку по текущим измерениям. Запишем (2) следующим образом
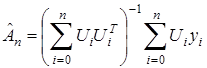 (3)
(3)
Здесь индекс 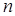 у оценки
у оценки 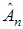 указывает на объем экспериментальных данных, используемых при ее вычислении. Выражение (3) введено чисто формально в том отношении, что проблема обращаемости матрицы в (3) не обсуждается, так как в последующем она легко снимается.
указывает на объем экспериментальных данных, используемых при ее вычислении. Выражение (3) введено чисто формально в том отношении, что проблема обращаемости матрицы в (3) не обсуждается, так как в последующем она легко снимается.
Воспользуемся следующим результатом, получившим название леммы обращения.
Леммы обращения. Пусть матрицы 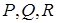 таковы, что образуют невырожденную матрицу
таковы, что образуют невырожденную матрицу 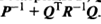 . Тогда справедливо представление
. Тогда справедливо представление
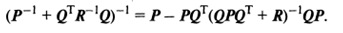 (4)
(4)
Обозначим
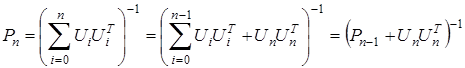
Воспользовавшись леммой об обращении матрицы, представим
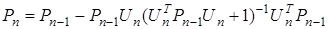 (5)
(5)
Тогда (3) запишем в виде:
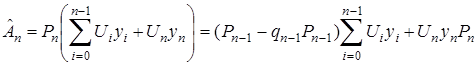 ,
,
где 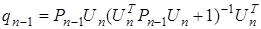 .
.
Так как
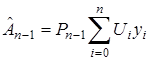 ,
,
то
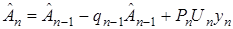 . (6)
. (6)
Учитывая введенные обозначения, имеем:
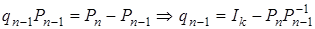 ,
,
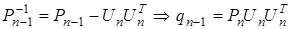 ,
,
где 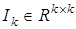 — единичная матрица.
— единичная матрица.
Тогда (6) преобразуем к виду
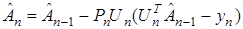 . (7)
. (7)
Итак, окончательно получаем
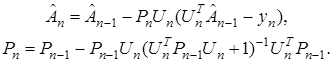 (8)
(8)
Совокупность выражений (8) принято называть рекуррентным методом наименьших квадратов (РМНК).
Вычисления по этому методу организуются следующим образом.
1. Полагаем 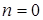 .
.
2. Задаем начальное приближение 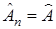 ,
, 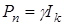 , где
, где 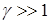 .
.
3. Из (5) находим 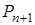 .
.
4. Из (7) находим 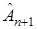 .
.
5. Полагаем 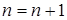 .
.
6. Если 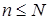 , то переходим к шагу 3, иначе заканчиваем работу процедуры.
, то переходим к шагу 3, иначе заканчиваем работу процедуры.
Если ввести невязку 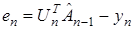 , то (7) можно записать следующим образом
, то (7) можно записать следующим образом
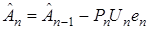 . (9)
. (9)
Рассмотрим частный случай алгоритма (9)
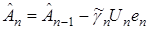 , (10)
, (10)
где 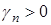 — некоторое число, обеспечивающее сходимость алгоритма.
— некоторое число, обеспечивающее сходимость алгоритма.
Выбор параметра 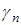 осуществляется следующим образом. Введем критерий
осуществляется следующим образом. Введем критерий
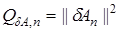 , (11)
, (11)
который характеризует отклонение получаемых оценок 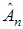 от неизвестных параметров системы
от неизвестных параметров системы 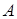 . Найдем
. Найдем 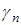 из условия
из условия
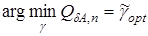 .
.
Запишем (10) относительно параметрической невязки 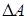
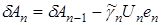 . (12)
. (12)
Подставляя (12) в (11) получим
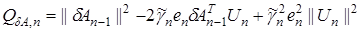 .
.
Достаточное условие минимума имеет вид
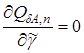
или в развернутом виде
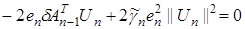 ,
,
откуда учитывая, что 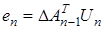 , получаем
, получаем
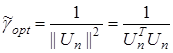 . (13)
. (13)
Подставляя (13) в (10) получаем так называемый алгоритм Качмажа
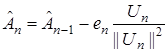 . (14)
. (14)
При наличии возмущений на выходе системы, в (14) вводят параметр 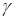 для обеспечения устойчивости (сходимости) алгоритма (14)
для обеспечения устойчивости (сходимости) алгоритма (14)
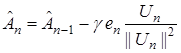 . (15)
. (15)
Условие сходимости (15) записывается следующим образом
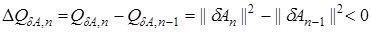 .
.
После несложных преобразований для 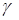 получим
получим
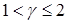 .
.
Схема адаптивной системы идентификации показана на рис. 1.
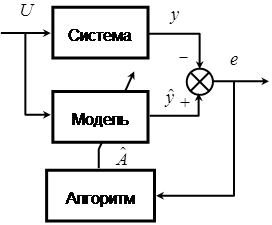
Рис. 1. Схема системы адаптивной идентификации
2. Вероятностные итеративные методы.
Метод стохастической аппроксимации
Вероятностные итеративные методы тесно применяются в случае, если на выходе системы действует случайное возмущение. Опишем способ их построения.
Рассмотрим функционал 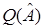 . Необходимое условие экстремума (минимума или максимума) имеет вид
. Необходимое условие экстремума (минимума или максимума) имеет вид
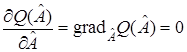 , (16)
, (16)
где 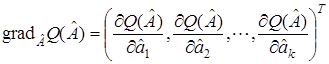 — градиент функционала.
— градиент функционала.
Уравнение оптимальности (16) в общем случае представляет собой нелинейное уравнение, и получить его решение аналитическим путем удается не всегда. Правда, в случае квадратичных критериев оптимальности и линейных ограничений первого рода нелинейные уравнения (2.2) превращаются в линейные, и как было показано на примере VYR для его решения можно применить правило Крамера. Поэтому для решения (16) часто применяют итерационные методы. Основная идея решения уравнения (16) с помощью регулярных итеративных методов состоит в следующем.
Запишем (16) в эквивалентной форме
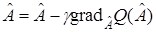 ,
,
где 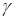 — некоторый скаляр, и будем искать оптимальный вектор
— некоторый скаляр, и будем искать оптимальный вектор 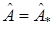 с помощью, последовательных приближений или итераций
с помощью, последовательных приближений или итераций
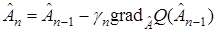 (17)
(17)
Значение 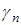 определяет величину очередного шага и зависит от номера шага
определяет величину очередного шага и зависит от номера шага 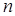 , вообще говоря, от векторов
, вообще говоря, от векторов 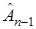 . При выполнении соответствующих условий сходимости, можно обеспечить выполнение условия
. При выполнении соответствующих условий сходимости, можно обеспечить выполнение условия
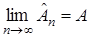 .
.
Методы определения 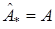 , основанные на соотношении (17), и называются итеративными методами. Поскольку выбор начального значения
, основанные на соотношении (17), и называются итеративными методами. Поскольку выбор начального значения 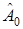 однозначно предопределяет дальнейшее значение последовательности
однозначно предопределяет дальнейшее значение последовательности 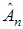 , то эти итеративные методы называют регулярными.
, то эти итеративные методы называют регулярными.
При наличии случайных возмущений критерий оптимизации имеет вид
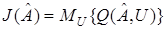 , (18)
, (18)
где 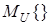 — математическое ожидание по
— математическое ожидание по 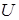 .
.
Считаем, что 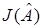 в явной форме неизвестен. Это значит, что плотность распределения
в явной форме неизвестен. Это значит, что плотность распределения 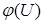 неизвестна, а известны лишь реализации
неизвестна, а известны лишь реализации 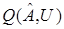 , которые зависят от стационарных случайных процессов или последовательностей
, которые зависят от стационарных случайных процессов или последовательностей 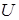 и вектора
и вектора 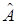 . Условие оптимальности (16) в этом случае имеет вид
. Условие оптимальности (16) в этом случае имеет вид
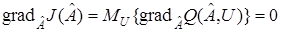 (19)
(19)
В (17) неизвестен градиент функционала, т. е. 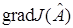 , а известны лишь реализации
, а известны лишь реализации 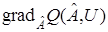 . При надлежащем выборе параметра
. При надлежащем выборе параметра 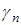 или в более общем случае матрицы
или в более общем случае матрицы 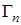 для решения задачи оценивания можно воспользоваться многими разновидностями регулярных методов, заменив в них градиент функционала
для решения задачи оценивания можно воспользоваться многими разновидностями регулярных методов, заменив в них градиент функционала 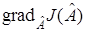 реализациями
реализациями 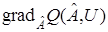 .
.
Таким образом, вероятностный алгоритм оптимизации или алгоритм адаптации можно представить в рекуррентной форме:
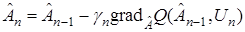 . (20)
. (20)
где 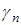 — специальным образом подбираемая последовательность неотрицательных чисел, называемых величинами рабочего шага.
— специальным образом подбираемая последовательность неотрицательных чисел, называемых величинами рабочего шага.
Алгоритм (20) называют алгоритмом стохастической аппроксимации, так как он позволяет получать оценки, минимизирующие функционал среднего риска (18).
В более общем виде алгоритм (20) записывается следующим образом
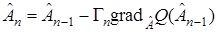 . (21)
. (21)
где 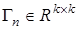 — квадратная матрица, обеспечивающая сходимость алгоритм (21) и получение состоятельных оценок. О них речь пойдет ниже.
— квадратная матрица, обеспечивающая сходимость алгоритм (21) и получение состоятельных оценок. О них речь пойдет ниже.
Заметим, что в случае квадратичного функционала 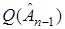 при использовании уравнения (1) градиент будет равен
при использовании уравнения (1) градиент будет равен
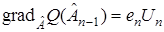 .
.
В результате получим алгоритм (12), который широко применяется в системах идентификации.
В настоящее время удалось обосновать свойства алгоритма (20) только в случае диагональной матрицы 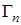 .
.
Приведем пример алгоритма стохастической аппроксимации (АСА).
2.1. Поиск корня неизвестной функции.
Алгоритм Роббинса—Монро
Первой по рекуррентный стохастический алгоритм предложили Роббинс и Монро для нахождении корня вещественной функции 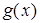 от вещественного аргумента
от вещественного аргумента 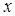 . Предполагалось, что функция неизвестна, но наблюдению экспериментатора доступны ее значения в выбираемых им точках, может быть, с помехами.
. Предполагалось, что функция неизвестна, но наблюдению экспериментатора доступны ее значения в выбираемых им точках, может быть, с помехами.
Если функция 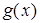 известна и непрерывно дифференцируема, то задача превращается в классическую из численного анализа. Для ее решения можно воспользоваться методом Ньютона, который генерирует последовательность оценок
известна и непрерывно дифференцируема, то задача превращается в классическую из численного анализа. Для ее решения можно воспользоваться методом Ньютона, который генерирует последовательность оценок 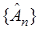 корня в функции
корня в функции 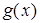 :
:
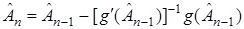 , (22)
, (22)
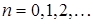 , или более простой, но менее эффективной, процедурой:
, или более простой, но менее эффективной, процедурой:
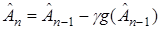 (23)
(23)
с фиксированным достаточно малым коэффициентом g.
Алгоритм (23) в отличие от (22) не требует вычисления производной функции 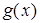 . Если начальное значение
. Если начальное значение 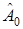 выбрано достаточно близко к
выбрано достаточно близко к 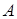 , то процедура гарантирует сходимость оценок к корню
, то процедура гарантирует сходимость оценок к корню 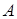 функции
функции 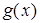 при предположениях о том, что
при предположениях о том, что 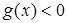 при
при 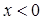 ,
, 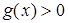 при
при 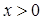 , производная функции
, производная функции 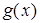 ограничена и
ограничена и 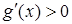 в некоторой окрестности точки
в некоторой окрестности точки 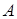 . Вообще говоря, эта процедура не требует и дифференцируемости функции
. Вообще говоря, эта процедура не требует и дифференцируемости функции 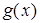 .
.
Теперь предположим, что точные значения функции 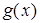 и ее производной неизвестны, а доступны только значения функции в выбираемых точках
и ее производной неизвестны, а доступны только значения функции в выбираемых точках 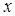 , но искаженные помехами.
, но искаженные помехами.
Роббинс и Монро предложили алгоритм:
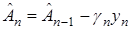 (24)
(24)
с некоторой выбираемой пользователем последовательностью положительных чисел 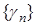 , стремящейся к нулю при
, стремящейся к нулю при 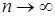 и удовлетворяющей условиям
и удовлетворяющей условиям
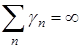 ,
, 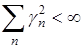 .
.
В (23) 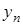 представляет собой зашумленное значение
представляет собой зашумленное значение 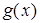 .
.
Дата добавления: 2017-02-13; просмотров: 5292;











