Робастные адаптивные алгоритмы

При практическом использовании того или иного алгоритма возможна ситуация, когда определенные наблюдения реализации случайной величины содержат очень большие значения. Как правило, в реальных системах при больших значениях параметров малоизвестны модели динамики или трудно что-либо предположить о статистических свойствах помех. В таких ситуациях модель часто определяют из соображений удобства использования или традиций. Однако нежелательно, чтобы одно большое по величине наблюдение существенно сказалось на вычислении текущей оценки. Для этого надо использовать робастные процедуры по аналогии с процедурами робастного статистического анализа. Опишем один из возможных подходов.

Пусть 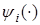, , 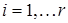ограниченные вещественные функции, заданные на вещественной оси, не убывающие и удовлетворяющие условиям:

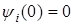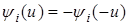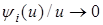, и при .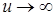

Один из наиболее часто используемых вариантов функций:

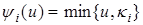для ,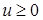

где 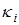— заданные константы.

Пусть, как и в (1), 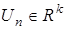— вектор входа,

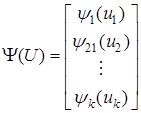
Обозначим через 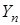какую-либо аппроксимацию градиента функции потерь 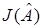в точке 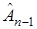. Тогда алгоритм

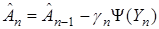
можно рассматривать как подходящую процедуру из робастной статистики. Ее важное преимущество состоит в том, что ограничен эффект больших значений в помехах наблюдения. Действительно, если чрезмерное значение помехи реализовалось в наблюдениях, то это наблюдение будет проигнорировано. Если алгоритм стохастической аппроксимации используется в реальной системе, а не в процессе компьютерного моделирования, и появились наблюдения с большими значениями, то, вообще говоря, надо постараться определить физическую причину такого значения, а не отказываться от учета этого наблюдения без всяких вопросов.

4. Метод адаптивных 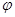-алгоритмов

Как следует из предыдущего изложения, качество работы адаптивных алгоритмов во многом зависит от действующих возмущений и различного рода не учитываемых факторов, таких как нестационарность, структурные возмущения, отклонение теоретических предпосылок от реальных условий и т. п. Все эти проблемы можно рассматривать из общих позиций, если выделить исследуемый объект из внешней среды. Это приводит к учету ограничений, накладываемых на систему. Один из подходов к учету ограничений был рассмотрен в § 2.2 при синтезе алгоритма (26). Для этого использовался метод множителей Лагранжа. Нетрудно заметить, что данный подход позволяет учесть не все существующие ограничения.

Прежде чем излагать данный метод синтеза, рассмотрим виды ограничений, которые могут применяться в система управления.