Наблюдаемый информационный портрет

МЕТОДЫ СТРУКТУРНОЙ ИДЕНТИФИКАЦИИ СТРУКТУРНАЯ ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ СИСТЕМ

Рассмотрим методы структурной идентификации, основанные на анализе экспериментальной информации в условиях неопределенности. Как уже отмечалось, до настоящего времени не предложено каких-либо регулярных методов выбора структуры модели. В основном работает интуиция исследователя, а также перебор нелинейностей, который задает исследователь, исходя из своего опыта и интуиции. Во всех указанных подходах проверка нелинейных составляющих модели производится на основе применения параметрических методов.

Сама по себе задача структурной идентификации динамических систем является сложной и распадается на ряд подзадач, которые сводятся к нахождению тех или иных структурных параметров системы. К наиболее важным из них относят:

· оценка порядка системы;

· оценка типа состояния равновесия;

· оценка собственных чисел матрицы состояния системы;

· выбор класса нелинейных операторов;

· оценка нестационарности системы;

· оценка запаздывания системы.

Ниже дается решение некоторых из этих подзадач.

Предварительный вывод о структуре система можно сделать на основе наблюдаемого информационного портрета.

Наблюдаемый информационный портрет

Рассмотрим систему

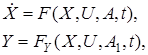(1)

где 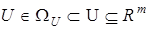— вход, 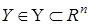— выход системы, 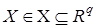— вектор состояния, 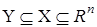, , 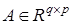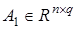— матрица параметров, 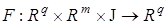— гладкая непрерывно дифференцируемая по 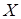и 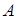вектор-функция, 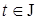, 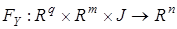— функция, задающая способ формирования выхода системы.

К множеству 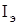будем относить не сами векторы 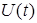и 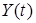, а их наблюдаемые (измеряемые) аналоги 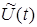, , 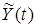которые получаются в результате применения операторов , :

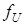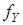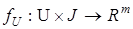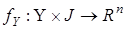, , (2)

отражающих ошибки измерения. Операторы 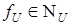, 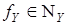определены на множествах 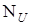, , 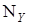характеризующих неопределенность процесса измерения.

В системах идентификации обычно используется множество 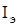. В силу применения операторов (2) получим множество наблюдений (измерений)

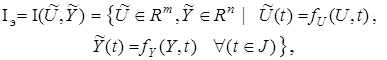(3)

В дальнейшем в отличие от (3) будем называть наблюдаемым информационным множеством системы (1).

Представим множество (4) в виде

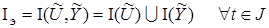. (4)

Определим бинарное отношение G между множествами U и Y системы (1): 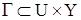. Назовем это множество портретом системы (1) в пространстве 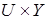. Множество G является дополнением множества X при проектировании его на 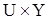. Соответствующий фазовый портрет системы (1) представим в виде

.

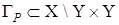
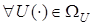Расширенным фазовым портретом системы будем называть отображение

.

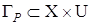
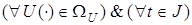Определение 1. Рассмотрим наблюдаемое информационное множество 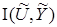(4) системы (1), определенное в пространстве 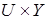. Тогда наблюдаемым информационным портретом системы (1) назовем бинарное отношение

.

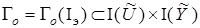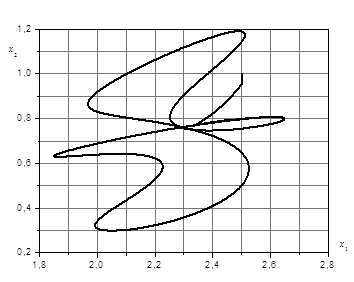
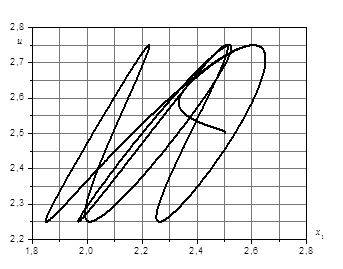
Наблюдаемый информационный портрет в отличие от фазового выходного портрета позволяет выявить новые свойства системы 1), которые дополняют динамическое множество X и позволяют определить ряд новых характеристик, полезных в процессе решения задачи структурной идентификации. На рис. 1 показаны примеры портретов для нестационарной системы второго порядка.

а)

б)

Рис. 1. Фазовый и наблюдаемый информационный портреты для нестационарной системы второго порядка: а) — фазовый портрет, б) — наблюдаемый информационный портрет