Предмет начертательной геометрии
В инженерной практике, исследовательской работе, в процессе передачи информации и во множестве других случаев человек использует различные модели. Модель никогда не повторяет объект или явление полностью и несет о них только основную информацию. Например: чертеж механизма передает информацию о размерах, форме, взаимодействии составных частей и т.д.; конспект лекций передает только содержание лекции, при этом не воспроизводя голос преподавателя, его жестикуляцию и т.д.; рисунок несет информацию о форме и цвете изображенного объекта и т.д.
Посредствам моделей информацию не только передают, но и перерабатывают: математик преобразовывает формулы, конструктор с помощью чертежа может усовершенствовать механизм, композитор пользуясь нотной записью, обрабатывает музыку. Таких примеров можно приводить очень много.
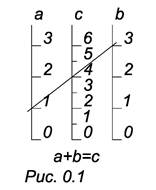 В наше время особое место занимают математические модели, которые делятся на два класса: аналитические и геометрические. К геометрическим моделям относятся: чертеж, рисунок, фотоснимок, рентгенограмма, номограмма и др. Номограмма это чертеж, который служит для облегчения и ускорения математических вычислений при технических расчетах. Наряду с понятием «номограмма» используется более точный термин – расчетно – геометрическая модель. Логарифмическая линейка, например, позволяет быстро производить умножение, деление и другие арифметические действия. Одной из простейших номограмм из выровненных точек является номограмма сложения. Работает она следующим образом: прикладываем линейку к точкам, соответствующим данным значениям, на шкалах а и b (рис. 0.1). На шкале С в точке пересечения шкалы линейки читаем ответ.
В наше время особое место занимают математические модели, которые делятся на два класса: аналитические и геометрические. К геометрическим моделям относятся: чертеж, рисунок, фотоснимок, рентгенограмма, номограмма и др. Номограмма это чертеж, который служит для облегчения и ускорения математических вычислений при технических расчетах. Наряду с понятием «номограмма» используется более точный термин – расчетно – геометрическая модель. Логарифмическая линейка, например, позволяет быстро производить умножение, деление и другие арифметические действия. Одной из простейших номограмм из выровненных точек является номограмма сложения. Работает она следующим образом: прикладываем линейку к точкам, соответствующим данным значениям, на шкалах а и b (рис. 0.1). На шкале С в точке пересечения шкалы линейки читаем ответ.
Расчетно – геометрические модели имеют широкое применение в инженерной практике. Конструировать их можно аналитически и геометрически.
Начертательная геометрия изучает модель для передачи и переработки геометрической информации.
Модели бывают однозначные (изоморфные) многозначные (гомоморфные).Примером однозначной модели студенческой группы является список фамилий, если в группе нет однофамильцев. Список группы чаще всего модель многозначная, так как одно и тоже имя может принадлежать нескольким студентам. Гомоморфные модели тоже несут информацию (иногда очень существенную) о изучаемом объекте.
Знакомство с начертательной геометрией начинают с построения гомоморфных геометрических моделей, после чего рассматривают способы позволяющие переходить к кэоморфным моделям.
Основным методом начертательной геометрии является способпроецирования. Определить проецирование, значит указать алгоритм, посредствам которого точки одного пространства сопоставляются точками другого пространства. Условимся обозначать одномерное пространство (линия) R1, двумерное пространство (поверхность) R2, трехмерное пространство R3, …….., n-мерное пространство Rn. В дальнейшем будем рассматривать проецирование трехмерных геометрических образов не плоскость.
1. Метод проецирования
1.1 Центральное проецирование
Посредством центрального проецирования осуществляется моделирование трехмерных геометрических образов на плоскость. Аппарат проецирования: плоскость проекции и центр проецирования (рис. 1.1)
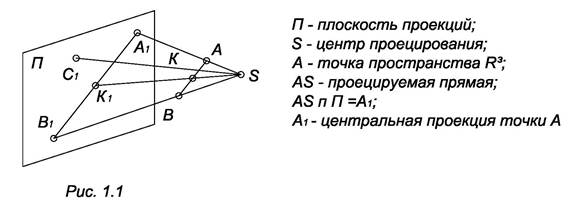
Проецирование рассмотренное на рис. 1.1 называется линейным, так как проецирующие образы – прямые (плоскости). В качестве проецирующих линий в некоторых случаях выбирают кривые линии. В этом случае проецирование называется нелинейным.
Предположим, что требуется спроецировать центральную прямую АВ. Нетрудно отметить, что все проецирующие прямые принадлежат плоскости SАВ (проецирующая плоскость). Эта плоскость пересекает плоскость проекции П по прямой А1В1. Следовательно, проекцией прямой линии в общем случае является прямая линия. В частном случае, прямая проецируется в точку, если она проходит через центр проецирования.
Заметим, что построенная таким образом на плоскости П модель пространства является гомоморфной (многозначной). Действительно, попытаемся по данной проекции С1 определить точку С в пространстве. Оказывается таких точек бесконечное множество, это все точки прямой S1C1. Но и эта модель несет некоторую информацию. Например, проекция точки определяет проецирующую прямую, которой принадлежит данная точка.
1.2 Параллельное проецирование
Если центр проецирования бесконечно удаленная точка, то проецирующие прямые параллельны между собой и проецирование называется параллельным. Чтобы задать параллельное проецирование, необходимо задать плоскость проецирования П и направление проецирования s. Направление проецирования не должно быть параллельно плоскости проекции (рис. 1.2) Если s перпендикулярно П, то проецирование называется ортогональным (рис. 1.3).
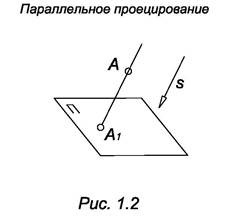
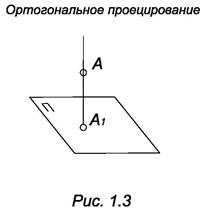
Таблица 1.1 Основные свойства проецирования
| Центральное проецирование | Параллельное проецирование | Ортогональное проецирование | |
| 1. Проекцией точки является точка. 2. Проекцией прямой линии является прямая линия. 3. Проекцией точки, принадлежащей некоторой прямой, является 4. точка принадлежащая проекции данной прямой. | |||
| 5. Если прямые параллельны, то при 6. параллельном проецировании их проекции 7. параллельны или совпадают, или обе прямые 8. проецируются в точки. 9. Отношение проекций отрезков, 10. принадлежащих параллельным прямым или 11. одной и той же прямой, равно отношению 12. самих отрезков. 13. Проекция фигуры не меняется при параллельном 14. переносе плоскости проекций. | |||
| 15. /А1В1/ = /АВ/ cosa, где а – угол 16. наклона АВ к плоскости проекций. | |||
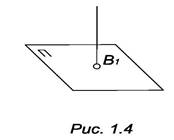 При проецировании трехмерных объектов на плоскость, т.е. при переходе от R3 к R2, получается гомоморфная модель объекта. Значит, рассматриваемые нами методы проецирования позволяют однозначно решить прямую задачу: по данному трехмерному объекту строить его проекцию на плоскость. Однако, обратная задача – по данной проекции воспроизвести (реконструировать) оригинал – однозначно не решается. Эта задача допускает бесконечное множество решений, т.к. каждую точку В1 плоскости П (рис. 1.4) можно считать проекцией любой точки проецирующей прямой, проходящей через В1.
При проецировании трехмерных объектов на плоскость, т.е. при переходе от R3 к R2, получается гомоморфная модель объекта. Значит, рассматриваемые нами методы проецирования позволяют однозначно решить прямую задачу: по данному трехмерному объекту строить его проекцию на плоскость. Однако, обратная задача – по данной проекции воспроизвести (реконструировать) оригинал – однозначно не решается. Эта задача допускает бесконечное множество решений, т.к. каждую точку В1 плоскости П (рис. 1.4) можно считать проекцией любой точки проецирующей прямой, проходящей через В1.
Чтобы добиться однозначности, следует дополнить проекционный чертеж, сделать его «обратимым», т.е. чертежом вполне определяющим данный геометрический объект. Существует много способов в дополнения проекционного чертежа. Остановимся на некоторых из них.
1.3 Способы дополнения проекционного чертежа
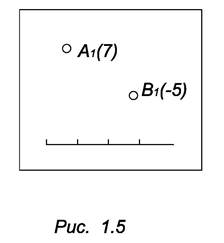 Проекции с числовыми (высотными) отметками (рис. 1.5). Число, стоящее в скобках рядом с обозначением проекции точки, задает расстояние от данной точки до плоскости проекций. Если число положительное, значит точка находится перед плоскостью проекций, если отрицательное, то точка за плоскостью проекций.
Проекции с числовыми (высотными) отметками (рис. 1.5). Число, стоящее в скобках рядом с обозначением проекции точки, задает расстояние от данной точки до плоскости проекций. Если число положительное, значит точка находится перед плоскостью проекций, если отрицательное, то точка за плоскостью проекций.
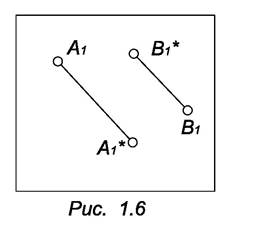
Векторные чертежи (способ Е.С. Федорова) (рис. 1.6.). Расстояние от точки до плоскости проекций задается посредством отрезков на плоскости проекций, начало отрезка совпадает с проекцией данной точки. Такие отрезки называются высотными. Они параллельны между собой. По направлению отрезка можно судить о том, где находится данная точка, перед плоскостью или за ней. Например, точка А – перед плоскостью проекций, В – за плоскостью проекций.
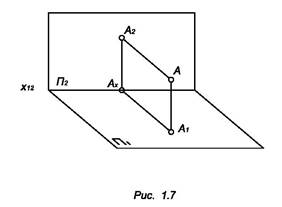
Аксонометрические проекции (рис. 1.7). Для получения аксонометрической проекции необходимо выполнить следующие действия:
1. Связать изображаемый объект с прямоугольной декартовой системой координат. Тогда для каждой точки можно построить координатную ломаную линию.
2. Спроецировать параллельно объект вместе с координатными осями на плоскость проекций, которая называется аксонометрической. Проекции осей координат называются аксонометрическими осями. Проекции масштабных отрезков называются аксонометрическими масштабами. Проекции координатной ломанной линии называется аксонометрической координатной ломаной.
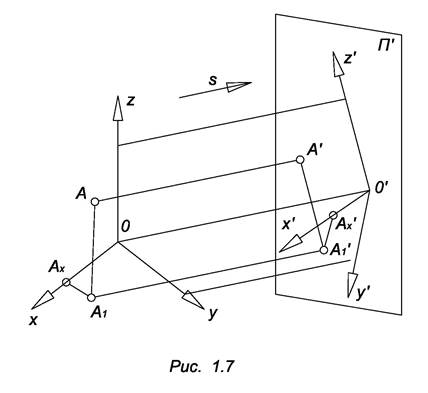 X’, Y’, Z’ – аксонометрические оси.
X’, Y’, Z’ – аксонометрические оси.
О’А’x А’1 А’ – аксонометрическая координатная ломаная линия.
А’ – аксонометрическая проекция точки А.
А’1 – вторичная проекция точки А, или аксонометрическое изображение проекции данной точки на плоскость xОy.
Однозначность аксонометрической проекции достигается с помощью задания аксонометрической ломанной линии или вторичной проекции изображенного объекта.
Комплексный чертеж
Этот способ получил наибольшее применение в технической практике. Однозначность модели достигается посредством использования двух связанных проекций геометрического объекта. Существует много способов образования комплексного чертежа. Познакомимся с одним из них.
1.4 Порядок построения комплексного чертежа.
Для построения комплексного чертежа необходимо выполнить следующие действия:
1. Выбрать две взаимно перпендикулярные плоскости П1 и П2 (рис. 1.8).
 П1 – горизонтальная плоскость проекций;
П1 – горизонтальная плоскость проекций;
П2 – фронтальная плоскость проекций;
П1П П2 = X12, где X12 – ось проекций.
2. Геометрический объект, например точка А, проецируется ортогонально на каждую плоскостей проекций.
А1 – горизонтальная проекция точки А;
А2 – фронтальная проекция точки А;
АА1 ┴ П1, следовательно, А2Аx ┴ X12,
А А2 ┴ П2, следовательно, , А1Аx ┴ X12,
/ А2 Аx/ = /АА1/ - высота точки, / А1 Аx/ = /АА2/ - глубина точки.
3. Плоскости проекций совмещают с плоскостью чертежа (рис. 1.9).
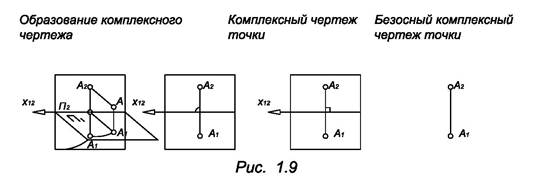
Полученный чертеж является обратным. Действительно, если фронтальной проекции А1 поставить перпендикуляр к плоскости чертежа и от точки А2 отложить на этом перпендикуляре, отрезок равный глубине точки, то однозначно определиться положение точки А. Т.о. изоморфной моделью точки пространства R3 является пара связанных точек плоскости.
1.5 Проекции прямоугольных осей координат на комплексном чертеже
В начертательной геометрии чаще пользуются правой прямоугольной системой координат (рис. 1.10). Относительно плоскостей проекций оси координат целесообразно располагать следующим образом: Оx║П1, Оz║П2, Оx║П2 и Оy║П1 (рис. 1/11). В частном случае, если нет необходимости на чертеже рассматривать точки с отрицательным значением координат y и z, проекции О1X1 и О2X2 могут совпадать.
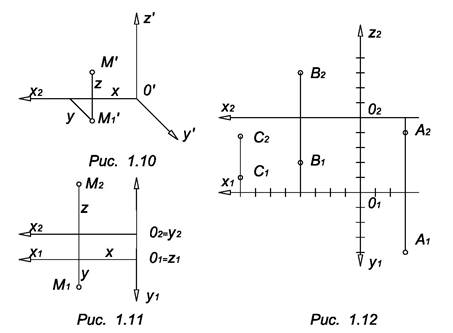
На рис. 1.12 дан комплексный чертеж точек А (-3, 4, -1); В (4, -2, 3); С (6, -1, -1).
В предыдущих примерах в качестве геометрического объекта рассматривались отдельные точки. Заметим, что для одной точки выбор плоскостей проекций не имеет значения, но для решения задач, в условия которых включены прямые, плоскости и др. объекты, выбор той или другой плоскости проекций может упростить или усложнить решение задачи. Например, в некоторых случаях задача упрощается, если плоскость проекций выбирать параллельно, или перпендикулярно данным геометрическим объектам. Переход от данной системы плоскостей проекций к новой можно осуществлять с помощью методов преобразования комплексного чертежа, самым распространенным на которых является метод замены плоскостей проекций.
1.6 Метод замены плоскостей проекций
 Метод замены плоскостей проекций состоит в переходе от данной системы плоскостей (старая система) к новой системе взаимно перпендикулярных плоскостей проекций. Положение самого объекта в пространстве остается неизменным.
Метод замены плоскостей проекций состоит в переходе от данной системы плоскостей (старая система) к новой системе взаимно перпендикулярных плоскостей проекций. Положение самого объекта в пространстве остается неизменным.
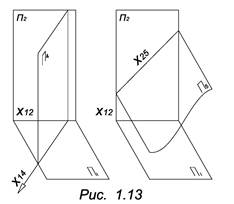
Иногда для решения задач достаточно заменить только одну из данных плоскостей проекций, например, плоскость П2 на плоскость П4, П4 ┴ П1. Или плоскость П1 на плоскость П5, П5 ┴ П2, (рис. 1.13). Этот метод применяется так же для построения дополнительной проекции, если необходимо на чертеже полнее изобразить геометрический объект.
Рассмотрим подробнее метод на примере построения дополнительной проекции точки (рис. 1.14 и рис. 1.15). Заметим, что применяя метод замены плоскостей проекций, следует фиксировать ось проекций на комплексном чертеже.
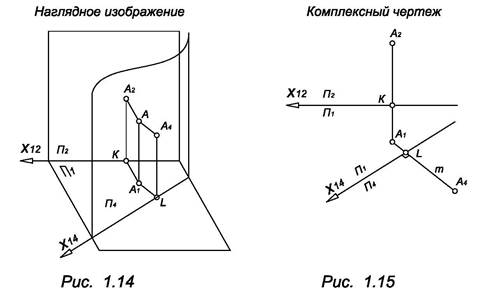
А – точка в пространстве. А1 и А2 соответственно горизонтальная и фронтальная проекция точки А. А4 – проекция точки А на плоскость П4, т.е. дополнительная проекция точки А. K и L точки на проекционных осях.
Из чертежа видно, что А2КА1А и А А1LА – прямоугольники следовательно, /А2К/ = /АА1/ = /А4L/. Проецирование ортогональное, значит прямые А1L, А4L, и X14 взаимно перпендикулярны. Пользуясь этими свойствами, легко построить дополнительную проекцию на комплексном чертеже (см. рис. 1.15).
При построении дополнительной проекции точки целесообразно пользоваться следующим алгоритмом:
1. Выбирается дополнительная плоскость проекций П4. П4 перпендикулярна одной из данных плоскостей проекций, на нашем чертеже П4 ┴ П1. П4П П1 – X14, прямую X14 назовем новой осью проекций.
2. Через проекцию точки А1 следует провести новую линию проекционной связи m, m ┴ X14.
3. На этой линии от точки L следует отложить отрезок LA4, / LA4/ = /А2К/. А1 – дополнительная проекция точки А.
Особого внимания заслуживает случай, когда дополнительная проекция перпендикулярна к плоскостям П1 и П2 (рис. 1.16).
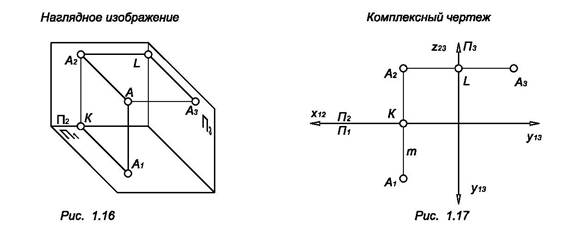
В черчении изображение на плоскости П3 относится к основным видам. Плоскость П3 называется профильной плоскостью проекций. А3 – профильная проекция точки А. Чтобы построить А3 по данным А1 и А2 следует выполнить такие действия:
1. Провести линию проекционной связи А2L, А2L ┴ Z23 (рис. 1.17)
2. Отложить на этой линии от оси Z23 отрезок LА3, / LА3/ = / КА1/.
Для решения более сложных задач метод замены плоскостей проекций можно применять неоднократно. Этот метод наряду с другими методами геометрического моделирования применяется во многих областях науки и техники. С помощью метода замены плоскостей проекций можно решать почти 90% задач нашего курса. Иногда мы пользуемся этим методом неосознанно, выделяя частные случаи на более общих в той или иной теории.
2. Комплексный чертеж прямой и плоскости и их аналитические модели
2.1 Комплексный чертеж прямой
На комплексном чертеже прямая может быть задана проекциями двух ее точек (рис. 2.1) или проекциями отрезка (рис. 2.2).
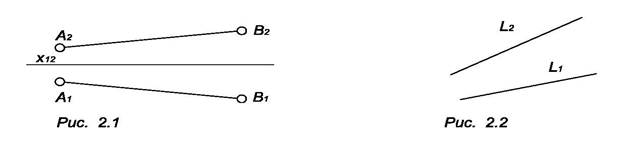
Прямые не параллельны и не перпендикулярны ни одной из плоскостей проекций, называются прямыми общего положения. Прямые общего положения бывают восходящими или нисходящими.
Восходящая прямая по мере удаления от наблюдателя поднимается вверх. Например, прямая L (см. рис. 2.2).
Нисходящая прямая по мере удаления от наблюдателя понижается. Например, прямая АВ (см. рис. 2.1).
Если прямая параллельна или перпендикулярна одной из плоскостей проекций, то она называется прямой частного положения.
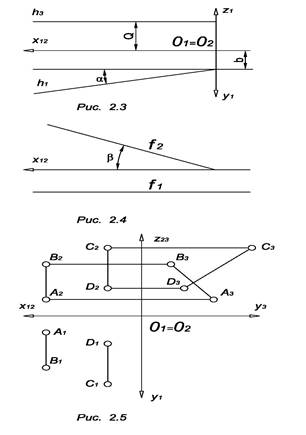
Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня (рис. 2.3).
h1 ║ x12, следовательно, высоты всех точек этой прямой равны между собой и h ║ П1. Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью.
Отрезок горизонтальной прямой на плоскость П1 проецируется в натуральную величину. А – угол наклона h к плоскости П2. f1 ║ x12, следовательно, глубины всех точек этой прямой равны между собой и f ║ П2. Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью. Отрезок фронтальной прямой на плоскость П2 проецируется в натуральную величину. Β – угол наклона f к плоскости П1 (рис. 2.4). Прямые АВ и СD на рис.2.5 параллельны плоскости П3 и называются профильными прямыми.
Прямые, перпендикулярные к одной из плоскостей проекций, называются проецирующими прямыми (рис. 2.6).
АВ ┴ П1, следовательно, на плоскость П1 АВ проецируется в точку. Прямая АВ называется горизонтально проецирующей. CD ┴ П2, следовательно, на фронтальную плоскость проекций CD проецируется в точку. Прямая CD называется фронтально проецирующей.
2.2 Аналитическая модель прямой
 Известно, что плоскости прямая может быть задана линейным (первой степени) уравнением с двумя неизвестными. В общем случае это уравнение имеет вид: ax + by + c =0, где x, у – независимые переменные, a, b, с – коэффициенты. Разделив обе части на С, получим уравнение
Известно, что плоскости прямая может быть задана линейным (первой степени) уравнением с двумя неизвестными. В общем случае это уравнение имеет вид: ax + by + c =0, где x, у – независимые переменные, a, b, с – коэффициенты. Разделив обе части на С, получим уравнение  x +
x +  у +1 = 0 или а1x + b1y + 1 = 0. Линейное уравнение можно задать так же в следующем виде:
у +1 = 0 или а1x + b1y + 1 = 0. Линейное уравнение можно задать так же в следующем виде:
 +
+  = 1 или y = kx +m.
= 1 или y = kx +m.
На комплексном чертеже пространственная прямая задается двумя проекциями, следовательно, для получения аналитической модели пространственной прямой достаточно задать уравнение ее проекций. Например, прямая L описывается системой из двух линейных уравнений (рис. 2.7):
 +
+ 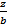 = 1;
= 1;
Прямая h на рис. 2.3 может быть задана системой уравнений:
z = 0. y = x tg + b.
Прямая CD на рис. 2.6 – системой: x = а, z = c.
2.3 Взаимное расположение линейных геометрических элементов
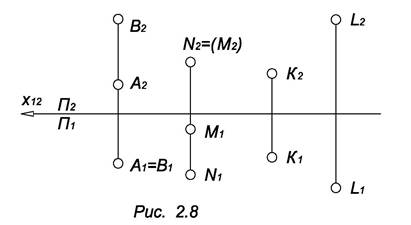 Линейными геометрическими элементами называются: точка – R0, прямая R1, плоскость – R2, трехмерное пространство – R3 и т.д. Взаимное расположение точек рассмотрим на следующем примере. Точки А и В расположены на одном перпендикуляре к горизонтальной плоскости проекций, их горизонтальные проекции совпадают (рис. 2.3). Такие точки называются горизонтально конкурирующими. По чертежу видно, что точка В выше точки А и на горизонтальной проекции точка А – невидимая. Точка М и N расположены на одном перпендикуляре к фронтальной плоскости проекций, поэтому фронтальные проекции этих точек совпадают. Такие точки называются фронтально конкурирующими. Из чертежа видно, что N ближе М, т.е. точка М на фронтальной проекции – невидимая. Про точки К и L можно сказать, что L расположена ближе, выше и правее точки К.
Линейными геометрическими элементами называются: точка – R0, прямая R1, плоскость – R2, трехмерное пространство – R3 и т.д. Взаимное расположение точек рассмотрим на следующем примере. Точки А и В расположены на одном перпендикуляре к горизонтальной плоскости проекций, их горизонтальные проекции совпадают (рис. 2.3). Такие точки называются горизонтально конкурирующими. По чертежу видно, что точка В выше точки А и на горизонтальной проекции точка А – невидимая. Точка М и N расположены на одном перпендикуляре к фронтальной плоскости проекций, поэтому фронтальные проекции этих точек совпадают. Такие точки называются фронтально конкурирующими. Из чертежа видно, что N ближе М, т.е. точка М на фронтальной проекции – невидимая. Про точки К и L можно сказать, что L расположена ближе, выше и правее точки К.
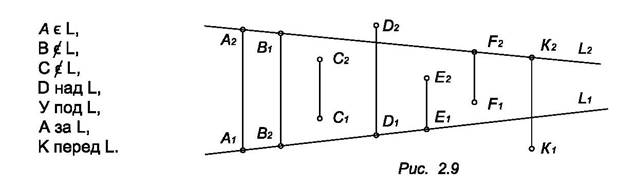
Принадлежность точки и прямой (рис. 2.9) определяются свойством проецирования 3 (Таблица 1.1).
Если прямая задана уравнениями, то значения координат точки, принадлежащей прямой, должны удовлетворять этим уравнениям. Например, точка А (3; 1; 0,75) принадлежит прямой: 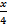 +
+  = 1,
= 1, 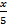 +
+ 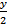 = 1, т.к.
= 1, т.к.  +
+ 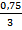 = 1,
= 1,  +
+ 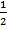 = 1.
= 1.
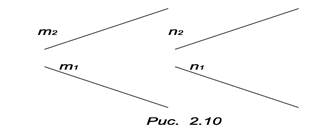 Параллельность прямых на чертеже определяется свойством 5 параллельного проецирования (рис. 2.10). Следует учитывать, что в некоторых частных случаях проекции не парралельных прямых могут быть параллельны, например, прямые АВ и CD на рис. 2.5.
Параллельность прямых на чертеже определяется свойством 5 параллельного проецирования (рис. 2.10). Следует учитывать, что в некоторых частных случаях проекции не парралельных прямых могут быть параллельны, например, прямые АВ и CD на рис. 2.5.
Рассмотрим проекции пересекающихся и скрещивающихся прямых (рис. 2.11). Прямые а и b имеют общую точку М, следовательно, они пересекаются. Скрещивающиеся прямые с и d не имеют общих точек. Точки N и K, L и Н, принадлежащие этим прямым, являются конкурирующими.
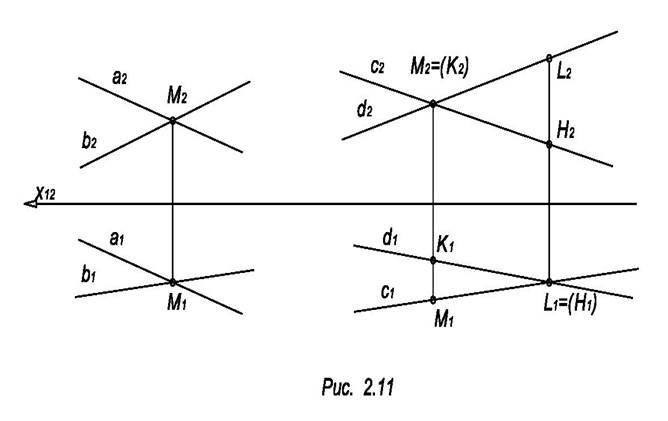
2.4 Комплексный чертеж плоскости
Плоскость в пространстве может быть задана: тремя точками, прямой и точкой, двумя параллельными прямыми, двумя пересекающимися прямыми и плоской фигурой. На комплексном чертеже плоскость задается проекциями перечисленных наборов геометрических элементов (рис. 2.12, 2.13, 2.14, 2.15, 2.16).
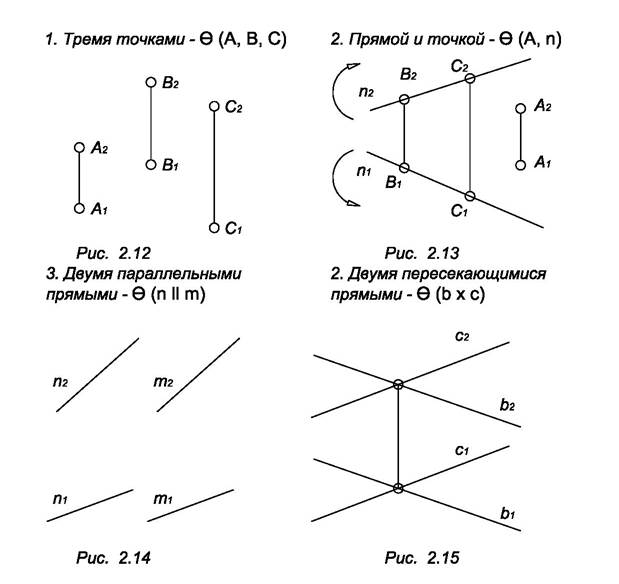
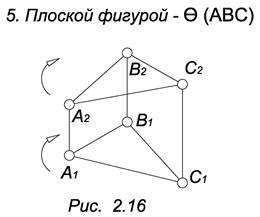
Если не параллельна и не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения. Плоскости общего положения бывают восходящими и нисходящими.
Если плоскость по мере удаления от наблюдателя поднимается вверх, то она называется восходящей. Чтобы избежать недоразумений, удаление надо производить по профильной прямой, принадлежащей плоскости. На комплексном чертеже восходящей плоскости обе проекции треугольника, ей принадлежащего, ориентировано одинаково (рис. 2.16), а для нисходящей – противоположно (рис. 2.13).
Если плоскость параллельна или перпендикулярна одной плоскостей проекций, то она называется плоскостью частного положения. Различают следующие виды плоскостей частного положения:
1. 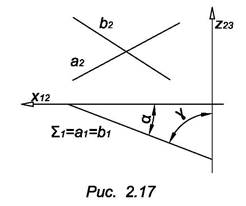 Плоскость, перпендикулярная к горизонтальной плоскости проекций, называется горизонтально проецирующей плоскостью. Все точки и прямые такой плоскости на горизонтальную плоскость проекций проецируются в прямую, например, Z1 (рис. 2.17) – проекция плоскости
Плоскость, перпендикулярная к горизонтальной плоскости проекций, называется горизонтально проецирующей плоскостью. Все точки и прямые такой плоскости на горизонтальную плоскость проекций проецируются в прямую, например, Z1 (рис. 2.17) – проекция плоскости 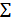 ,
,  ┴ П1; а,b ?
┴ П1; а,b ? 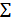 . Фронтальная и профильная проекции ее занимают соответственно все поле проекций П1 и все поле проекций П3. Очевидно, что а и ᵞ - углы наклона плоскости
. Фронтальная и профильная проекции ее занимают соответственно все поле проекций П1 и все поле проекций П3. Очевидно, что а и ᵞ - углы наклона плоскости 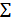 , к фронтальной и профильной плоскостям соответственно.
, к фронтальной и профильной плоскостям соответственно.
2. 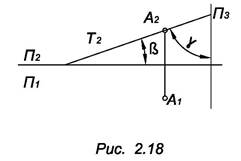 Плоскость, перпендикулярная к фронтальной плоскости проекций, называется фронтально проецирующей плоскостью, ее фронтальная проекция является прямой, а горизонтальная и профильная проекции занимают соответственно все поле проекций П1 и все поле проекций П3 (рис. 2.18). Фронтально проецирующая плоскость Т вполне определяется ее одной проекцией Т2. Углы β и u измеряют углы наклона плоскости к плоскостям проекций П1 и П3 соответственно, А ? Т.
Плоскость, перпендикулярная к фронтальной плоскости проекций, называется фронтально проецирующей плоскостью, ее фронтальная проекция является прямой, а горизонтальная и профильная проекции занимают соответственно все поле проекций П1 и все поле проекций П3 (рис. 2.18). Фронтально проецирующая плоскость Т вполне определяется ее одной проекцией Т2. Углы β и u измеряют углы наклона плоскости к плоскостям проекций П1 и П3 соответственно, А ? Т.
3. 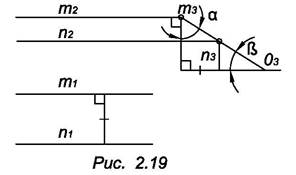 Плоскость, перпендикулярная к профильной плоскости проекций, называется профильно проецирующей плоскостью, ее профильная проекция является прямой, а горизонтальная и фронтальная проекции занимают соответственно все поле проекций П1 и все поле проекций П2 (рис. 2.19). Профильно проецирующая плоскость О вполне определяется ее одной проекцией О3. Углы а и β измеряют углы наклона плоскости О к плоскостям проекций П1 и П2 соответственно. n ? О, m ? О.
Плоскость, перпендикулярная к профильной плоскости проекций, называется профильно проецирующей плоскостью, ее профильная проекция является прямой, а горизонтальная и фронтальная проекции занимают соответственно все поле проекций П1 и все поле проекций П2 (рис. 2.19). Профильно проецирующая плоскость О вполне определяется ее одной проекцией О3. Углы а и β измеряют углы наклона плоскости О к плоскостям проекций П1 и П2 соответственно. n ? О, m ? О.
4. Плоскость, параллельную какой – нибудь плоскости проекций, называют плоскостью уровня, так как все точки этой плоскостью одинаково удалены от соответствующей плоскости проекций (рис. 2.20).
Плоскость Г, параллельную горизонтальной плоскости проекций, называют горизонтальной плоскостью уровня, а, b ? Г.
Плоскость Ф, параллельную фронтальной плоскости проекций, называют фронтальной плоскостью уровня, А, l ?Ф.
Плоскость Р, параллельную профильной плоскости проекций называют профильной плоскостью уровня.
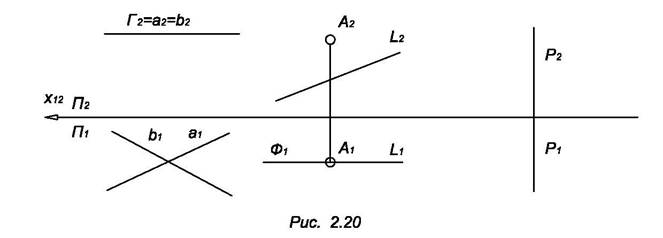
Очевидно, что каждая плоскость уровня является в то же время проецирующей плоскостью. Фигуры, принадлежащие горизонтальной плоскости Г, фронтальной плоскости Ф или профильной плоскости Р проецируется без искажения соответственно на плоскость проекций П1, П2 или П3.
2.5 Взаимное положение точки, прямой и плоскости
 Задачи на взаимное положение геометрических элементов называются позиционными.
Задачи на взаимное положение геометрических элементов называются позиционными.
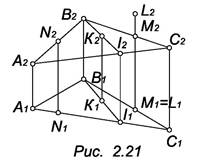
 Точка принадлежит плоскости, если она принадлежит какой – либо прямой этой плоскости. Например, точка К ? G (А, В, С), т.к. К ? В1 и G1 ? О (А, В, С) (рис. 2.21). Очевидно, что N не принадлежит плоскости О, т.к. точка N не принадлежит ни одной из двух прямых АВ или АС. Про точку N можно сказать, что она расположена над плоскостью О, т.к. она расположена над прямой АС. Известно, что точка M ? О, а точка L расположена над точкой М, следовательно, точка L находится над плоскостью О.
Точка принадлежит плоскости, если она принадлежит какой – либо прямой этой плоскости. Например, точка К ? G (А, В, С), т.к. К ? В1 и G1 ? О (А, В, С) (рис. 2.21). Очевидно, что N не принадлежит плоскости О, т.к. точка N не принадлежит ни одной из двух прямых АВ или АС. Про точку N можно сказать, что она расположена над плоскостью О, т.к. она расположена над прямой АС. Известно, что точка M ? О, а точка L расположена над точкой М, следовательно, точка L находится над плоскостью О.
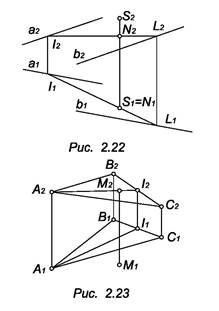
Задача. Дана восходящая плоскость Э (а ║b), построить точку S над плоскостью, если известна ее горизонтальная проекция S1 (рис. 2.22).
Точка S2 должна располагаться над вспомогательной прямой 12, принадлежащей плоскости О и следовательно, над точкой N ? 12. Очевидно, что задача имеет бесконечное множество решений.
Обратная задача. Определить положение точки М относительно плоскости R (А, В, С). М ближе R, т.к. М ближе А1 ? R (рис. 2.23).
Задача. Построить проекции треугольной пирамиды, основание которой принадлежит данной плоскости Q, а вершина расположена над плоскостью. Определить видимость ребер пирамиды.
Эта задача состоит из трех элементарных задач.
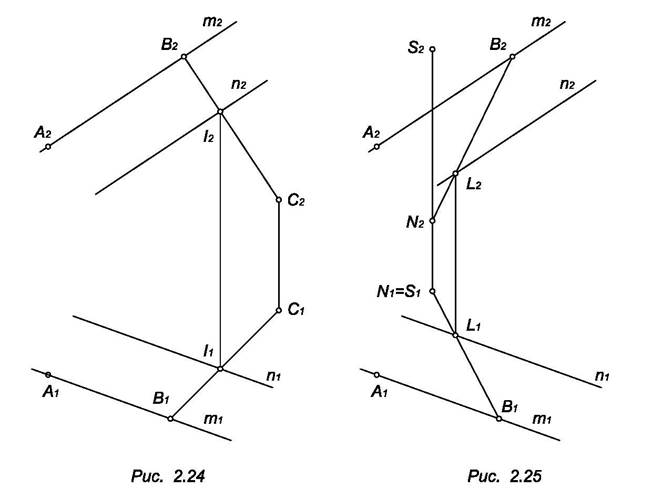
1. Построить вершины А, В, С в плоскости Q. Точки А и В выберем на прямой m, а точку С на вспомогательной прямой В1 (рис. 2.24).
2. Построить точку S над плоскостью Q. Выберем некоторую точку N, принадлежащую Q. На рис. 2.25 эта точка принадлежит В2 ? Q. Точка S д.б. над точкой N.
Q (m ║ n) – нисходящая плоскость.
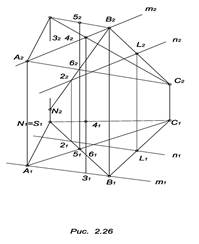
3. На рис. 2.26 повторены эти действия и через полученные точки проведены ребра искомой пирамиды.
Контурные ребра на всех плоскостях проекций всегда видимые.
Для определения видимости ребер АС и SB на горизонтальной плоскости проекций следует воспользоваться горизонтально конкурирующими точками 5 и 6 на этих ребрах. По фронтальной проекции видно, что точка 5 выше точки 6, следовательно, на горизонтальной проекции видимыми являются точка 5 и ребро АС, которому она принадлежит. Аналогично определяется на фронтальной проекции видимость ребер АВ и SC посредством фронтально конкурирующих точек 3 и 4.
2.6 Кривые линии и их проекции
Понятие о линиях как и о других геометрических объектах приобретается из опыта. Кривую линию можно рассматривать как границу части поверхности, или как результат пересечения двух поверхностей, или как множество последовательных положений непреровно перемещающейся в пространстве точки.
Положение точки на линии может быть определено одним параметром, следовательно, линия является однопараметрическим множеством точек..
Назовем два способа классификации кривых линий:
1. Кривые бывают плоские, пространственные и многомерные.
2. Кривые могут быть закономерными и незакономерными.
Закономерные кривые могут быть заданы и аналитически и графически. Незакономерные задаются только графически.
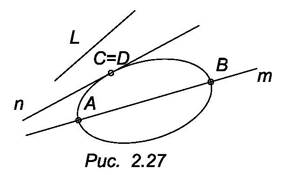 В зависимости от вида уравнения кривой закономерные кривые бывают алгебраические и транссидентные. Степень алгебраического уравнения определяет порядок кривой. Геометрически порядок плоской кривой определяется по числу точек пересечения ее с прямой, принадлежащей плоской кривой. Точки пересечения могут быть действительными и мнимыми. Например, эллипс пересекается с прямой m в двух действительных точках А и В, с прямой n в двух совпавших действительных точках, с прямой l в двух мнимых точках (рис. 2.27). Если составить уравнение эллипса и прямой m, то, решая их совместно, получим уравнение второго порядка, дискриминант которого положительное число. Во втором случае дискриминант равен нулю, а в третьем - дискриминант отрицателен.
В зависимости от вида уравнения кривой закономерные кривые бывают алгебраические и транссидентные. Степень алгебраического уравнения определяет порядок кривой. Геометрически порядок плоской кривой определяется по числу точек пересечения ее с прямой, принадлежащей плоской кривой. Точки пересечения могут быть действительными и мнимыми. Например, эллипс пересекается с прямой m в двух действительных точках А и В, с прямой n в двух совпавших действительных точках, с прямой l в двух мнимых точках (рис. 2.27). Если составить уравнение эллипса и прямой m, то, решая их совместно, получим уравнение второго порядка, дискриминант которого положительное число. Во втором случае дискриминант равен нулю, а в третьем - дискриминант отрицателен.
Проекции плоскости кривых линий обладает следующими основными свойствами:
1. В общем случае порядок плоской алгебраической кривой при параллельном проецировании не изменяется.
2. Бесконечно удаленные точки кривой проецируются в бесконечно удаленные точки ее проекций.
3. Касательная к кривой проецируется в касательную к ее проекции
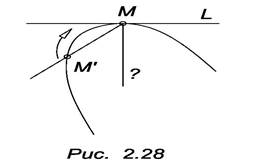 Касательной t в точке М плоской кривой l будем называть предельное положение секущей ММ’, когда М, оставаясь на линии l, стремиться к точке М (рис. 2.28). Нормалью n к кривой l в точке М называют прямую, принадлежащую плоской кривой и перпендикулярную к касательной в этой точке.
Касательной t в точке М плоской кривой l будем называть предельное положение секущей ММ’, когда М, оставаясь на линии l, стремиться к точке М (рис. 2.28). Нормалью n к кривой l в точке М называют прямую, принадлежащую плоской кривой и перпендикулярную к касательной в этой точке.
2.7 Линии второго порядка
В общем случае кривая второго порядка задается уравнением второго порядка вида:
Аx2 +By2 + Cxy + Dx + Ey + 1 = 0
(Если свободный член уравнения не равен 1, то обе части уравнения можно разделить на свободный член).
Следовательно, кривую второго порядка определяют пять параметров А, В, С, D, Е. Эти параметры можно вычислить, взяв координаты пяти точек данной кривой. Пусть известны точки: М1 (x1y1), М2 (x2y2), М3 (x3y3), М4 (x4y4) и М5 (x5y5). Для определения коэффициентов А, В, С, D, Е следует решить систему из пяти линейных уравнений:
Аx12 + Вy12 + Cx1y1 + Dx1 + Ey1 + 1 = 0
Аx22 + Вy22 + Cx2y2 + Dx2 + Ey2 + 1 = 0
Аx32 + Вy32 + Cx3y3 + Dx3 + Ey3 + 1 = 0
Аx42 + Вy42 + Cx4y4 + Dx4 + Ey4 + 1 = 0
Аx52 + Вy52 + Cx5y5 + Dx5 + Ey5 + 1 = 0
Следовательно, кривую второго порядка в общем случае можно задавать пятью точками или набором из пяти других геометрических элементов, например, двумя касательными и тремя точками. Подробнее с этим вопросом можно познакомиться по учебнику.
Если кривая второго порядка задана уравнением в общем виде, то пользуясь поворотом и переносом осей координат, ее уравнение можно привести к пяти частным случаям, которые перечислены в таблице 2.1.
Таблица 2.1 Уравнения. Определения и основные понятия кривых второго порядка
| Кривая | Основные понятия | Чертеж |
| Окружность x2 + y2 =R Множество точек равноудаленных от данной точки на данное расстояние Уравнение (x-a)2 + (y-b)2 = R2, где a, b – координаты центра, R – радиус. Если центр в начале координат, то x2 + y2 = R2 | /ОМ/ - радиус окружности 12 – диаметр окружности О – центр окружности (12) и (34) – перпендикулярные диаметры окружности t – касательная окружности (56) и (78) – ортогонально – сопряженные диаметры окружности (q10) – хорда ортогонально – сопряженная диаметру (78) | 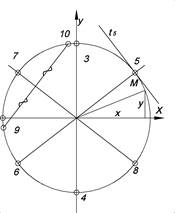
|
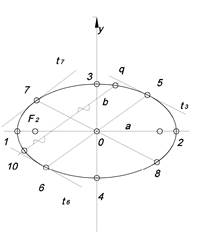
Эллипс
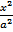 + +  = 1
Множество точек, сумма расстояний которых до двух данных точек F1 и F2, есть величина постоянная. = 1
Множество точек, сумма расстояний которых до двух данных точек F1 и F2, есть величина постоянная.
| (12) – большая ось эллипса
(34) – малая ось эллипса
С,b – большая и малая полуоси эллипса
О – центр эллипса
F1, F2 – фокусы эллипса
/О F1/ = /О F2/ = 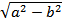 (56) и (78) – сопряженные диаметры эллипса
t5, t6 – касательные эллипса, сопряженные диаметру (56)
t5, t7 – сопряженные касательные
(910) – хорд, сопряженная диаметру (78)
(56) и (78) – сопряженные диаметры эллипса
t5, t6 – касательные эллипса, сопряженные диаметру (56)
t5, t7 – сопряженные касательные
(910) – хорд, сопряженная диаметру (78)
| 
|
| Парабола X2 = 2ру Множество точек, для которых расстояние до данной точки F и данной прямой d равны | О – вершина параболы OF – ось параболы t5, - касательная параболы (56) и t5, - сопряженные направления параболы F, d – фокус и директриса параболы. /EF/ = P | 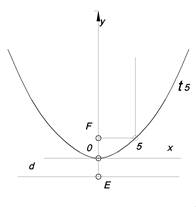
|
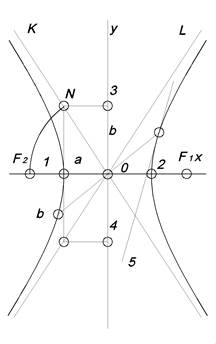
Гипербола
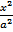 - -  = 1
Множество точек, разность расстояний которых до двух данных точек F1 и F2, есть величина постоянная. = 1
Множество точек, разность расстояний которых до двух данных точек F1 и F2, есть величина постоянная.
| 1,2 – действительные вершины гиперболы
3,4 – мнимые вершины гиперболы
(12) – действительная ось гиперболы
(34) – мнимая ось гиперболы
(02) – действительная полуось гиперболы
(03) – мнимая полуось гиперболы
OK и OL – асимптоты гиперболы
(56) и t – сопряженные направления гиперболы
F1 и F2 – фокусы гиперболы
/OF1/ = /OF2/ = /ON/ = 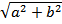
| 
|
Рассмотрим некоторые способы построения кривых второго порядка.
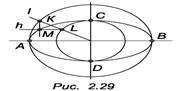
Задача. Построить эллипс по двум осям (рис. 2.29).
Даны:
АВ – большая ось эллипса
CD – малая ось эллипса
О – центр эллипса
1. Проводим две окружности с центром О и радиусом /ОА/ и /ОС/.
2. L – любая прямая проходящая через О.
Прямая l пересекает окружность в точках K и L.
3. Через точку K (K принадлежит большей окружности) проводим прямую f, параллельную малой оси. Через точку L (L принадлежит малой окружности) проводим прямую h, параллельную большой оси эллипса f ║h = М. М принадлежит эллипсу.
4. Меняя положение прямой l, получим множество точек эллипса, которые следует соединить плавной кривой линией.
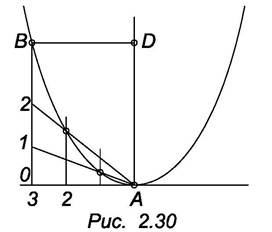
Задача. Построить параболу (рис. 2.30)
 Даны:
Даны:
А – вершина параболы
AD- направление оси
В – одна из точек.
1. Строим прямоугольник ACBD/
2. Отрезки АС и СВ делим на произвольное и одинаковое число равных частей и нумеруем точки деления как показано на рисунке.
3. Вершину А соединяем с точками деления отрезка СВ, а из точек деления отрезка АС проводим прямые, параллельные оси.
4. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы.
Вторую ветвь параболы можно построить, пользуясь симметрией относительно AD.
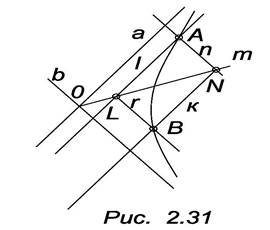
Задача. Построить гиперболу (рис. 2.31).
Даны:
a и b – асимптоты,
а П b = О,
А – некоторая точка гиперболы.
1. Через точку А проведем прямые n и l, параллельные асимптотам b и a соответственно.
2. Через центр гиперболы О проведем произвольную прямую m. m П n = N; m П l =L.
3. Через точку N проведем прямую k, k ║ а; и через точку L прямую r, r ║ b.
4. k П r = B, B – принадлежит искомой гиперболе.
Меняя положение прямой l, получим ряд точек гиперболы.
2.8 Пространственные кривые

Пространственные кривые задаются системой из двух уравнений y = f(x), z = u(x) или T (x, y, z) = 0, u (x, y, z) = 0, т.е. фактически уравнениями заданы две поверхности, пересечением которых определена кривая.
Для задания пространственной кривой на чертеже необходимы две проекции. На рис. 2.32 изображена пространственная кривая. Очевидно, что эта кривая имеет
| <== предыдущая лекция | | | следующая лекция ==> |
| Тяговые рельсовые цепи, заземления | | | Техническая характеристика пневматических переносных перфораторов |
Дата добавления: 2017-02-13; просмотров: 2458;











