Коническая зубчатая передача.
Конической зубчатой передачей называется зубчатая передача с пересекающимися осями, у зубчатых колёс которой аксоидные, начальные и делительные поверхности конические. Угол 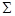 между осями ОО1 и ОО2 шестерни и колеса называется межосевым углом (рис 20.1)
между осями ОО1 и ОО2 шестерни и колеса называется межосевым углом (рис 20.1)
Если угол между осями равен 90°, то коническую зубчатую передачу называют ортогональной. В общем случае в не ортогональной передаче угол, дополненный до 180° к углу между векторами угловых скоростей 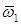 и
и 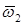 звеньев 1 и 2, называют межосевым углом
звеньев 1 и 2, называют межосевым углом 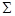 (рис. 12.1, a)
(рис. 12.1, a)
Связь между 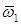 и
и 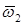 угловых скоростей 1 и 2 определяется соотношением:
угловых скоростей 1 и 2 определяется соотношением:
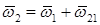 (20.1)
(20.1)
Если через точку О пересечения осей О1О и О2О провести вектор 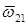 то он совпадет с мгновенной осью ОР относительного движения ведущего и ведомого звеньев и определит конические поверхности аксоидов, называемых начальными конусами. При обозначении параметров, относящихся к начальному конусу, используют индекс
то он совпадет с мгновенной осью ОР относительного движения ведущего и ведомого звеньев и определит конические поверхности аксоидов, называемых начальными конусами. При обозначении параметров, относящихся к начальному конусу, используют индекс 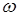 . Углы
. Углы 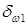 и
и 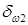 начальных конусов определяют при решении векторного соотношения (20.1) с использованием теоремы синусов (рис. 20.1, а):
начальных конусов определяют при решении векторного соотношения (20.1) с использованием теоремы синусов (рис. 20.1, а):
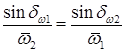
Отношение модулей угловых скоростей | 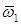 | и |
| и | 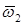 | является передаточным отношением:
| является передаточным отношением:
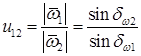 (20.3)
(20.3)
При заданных межосевом угле 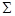 и передаточном отношении u12 углы начальных конусов определяют при совместном решении соотношений (20.2) и (20.3):
и передаточном отношении u12 углы начальных конусов определяют при совместном решении соотношений (20.2) и (20.3):
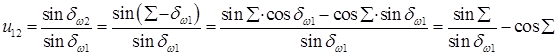
Искомые углы 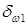 и
и 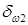 начальных конусов находят по формулам:
начальных конусов находят по формулам:
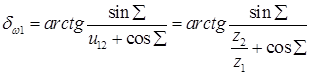 (20.4)
(20.4)
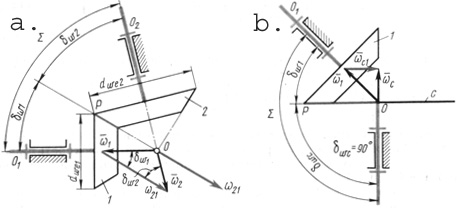
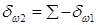 (20.5)
(20.5)
 |
Для ортогональной передачи при
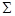 =90° соотношения (20.4) и (20.5) имеют частный вид:
=90° соотношения (20.4) и (20.5) имеют частный вид:
|
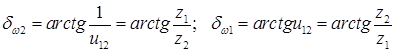 (20.6)
(20.6)
Частным случаем неортогональной передачи является плоская коническая передача, в которой поверхность одного из начальных колес является плоскостью и угол при вершине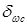 =90° (рис 20.1, б)
=90° (рис 20.1, б)
|
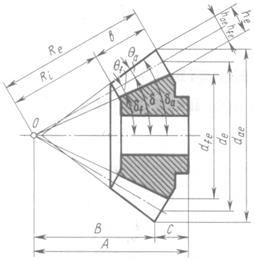 Параметры, относящиеся к плоскому коническому колесу, обозначают с добавлением индекса с (например: число зубьев плоского колеса zс, угловая скорость
Параметры, относящиеся к плоскому коническому колесу, обозначают с добавлением индекса с (например: число зубьев плоского колеса zс, угловая скорость 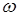 c). Формирование колес, размеров зубьев и расположение их элементов проводят относительно базовой конической поверхности на каждом колесе, называемой делительным конусом. При проектировании конических передач углы
c). Формирование колес, размеров зубьев и расположение их элементов проводят относительно базовой конической поверхности на каждом колесе, называемой делительным конусом. При проектировании конических передач углы  1и
1и  2 делительных конусов принимают совпадающими с углами
2 делительных конусов принимают совпадающими с углами 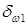 и
и  начальных конусов, что упрощает расчетные соотношения. Зубья образуют на колесе зубчатый венец, который располагается между конусом вершин с углом
начальных конусов, что упрощает расчетные соотношения. Зубья образуют на колесе зубчатый венец, который располагается между конусом вершин с углом  a и конусом впадин с углом
a и конусом впадин с углом  f (рис 20.2). При изготовлении заготовок и колес используют базовое расстояние А и размеры В до вершины конуса и С - до базовой плоскости.
f (рис 20.2). При изготовлении заготовок и колес используют базовое расстояние А и размеры В до вершины конуса и С - до базовой плоскости.
|
Поверхность, отделяющая зуб от впадины, называется боковой поверхностью зуба. Пересечение боковой поверхности зуба с соосной поверхностью называют линией зуба. Линия зуба может совпадать с образующей делительного соосного конуса (прямые зубья) или иметь угол 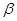 наклона линии зуба на делительной поверхности. Различают виды конических колес, отличающихся по форме линий зубьев на развертке делительного конуса (рис 20.3): a - с прямыми; b - тангенциальными; c - круговыми; d, e, f - криволинейными зубьями. Прямозубые передачи используют для работы при легких нагрузках и невысоких скоростях (обычно при частоте вращения <100 об/мин). Для работы в режиме максимальных нагрузок, при высоких скоростях и для обеспечения максимальной плавности работы и бесшумности используют передачи с криволинейными зубьями.
наклона линии зуба на делительной поверхности. Различают виды конических колес, отличающихся по форме линий зубьев на развертке делительного конуса (рис 20.3): a - с прямыми; b - тангенциальными; c - круговыми; d, e, f - криволинейными зубьями. Прямозубые передачи используют для работы при легких нагрузках и невысоких скоростях (обычно при частоте вращения <100 об/мин). Для работы в режиме максимальных нагрузок, при высоких скоростях и для обеспечения максимальной плавности работы и бесшумности используют передачи с криволинейными зубьями.
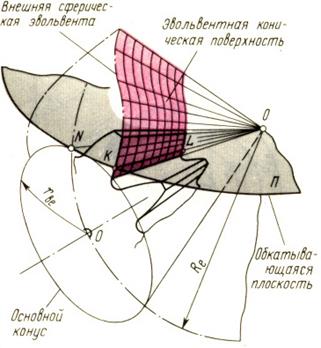 Образование боковой поверхности зубьев можно проследить по рис. 20.4. Плоскость П касается основного конуса и перекатывается по нему без скольжения. Любая прямая KL на обкатывающейся плоскости П в пространстве опишет коничес-кую эвольвентную поверхность, а любая точка
Образование боковой поверхности зубьев можно проследить по рис. 20.4. Плоскость П касается основного конуса и перекатывается по нему без скольжения. Любая прямая KL на обкатывающейся плоскости П в пространстве опишет коничес-кую эвольвентную поверхность, а любая точка
|
Радиус Re внешнего торцевого сечения называют внешним конусным расстоянием. Расстояние между внешним и внутренним торцевыми сечениями конического колеса называют шириной зубчатого венца и обозначают b (см. рис. 20.2).
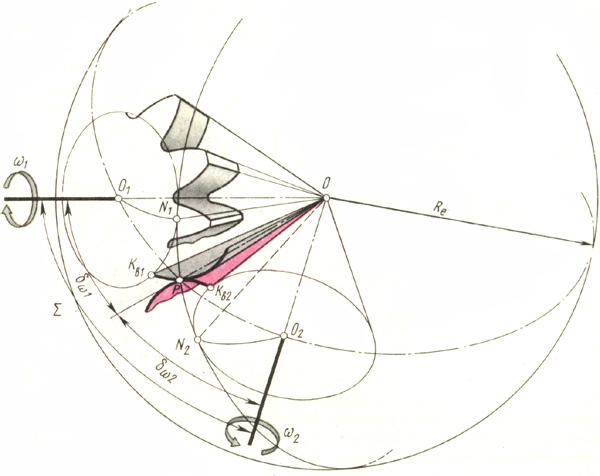
Взаимодействие сопряженных эвольвентных конических поверхностей при заданных начальных конусах представляет коническое эвольвентное зацепление (рис. 20.5).
Полюсная прямая РО, лежащая в плоскости N1ON2, касательной к основным конусам, может рассматриваться как образующая боковых поверхностей зубьев. Любые сопряженные сферические эвольвенты Э1 и Э2, имеют линию зацепления, расположенную на сфере (например, N1PN2) и являющуюся дугой большого круга сферы.
|
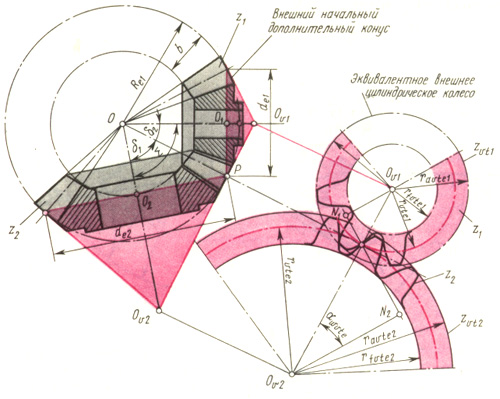
Взаимодействие сферических эвольвент описать в аналитической форме довольно сложно. Учитывая, что высотные размеры зубьев невелики по сравнению с радиусом сферы и профили зубьев расположены на узком сферическом поясе, используют инженерную методику расчета, которая заключается в использовании дополнительных конусов (рис. 20.6).
Дополнительным делительным конусом называют соосную коническую поверхность, образующая которого (например, РОv1 или Р0e2 на рис. 20.6) перпендикулярна образующей делительного конуса конического зубчатого колеса. Введение дополнительных конусов позволяет рассматривать взаимодействие профилей зубьев не на сфере, а на поверхности соприкасающихся со сферой дополнительных конусов. Если дополнительные конусы развернуть на плоскость, то профили зубьев становятся плоскими кривыми, достаточно близкими к обычным эвольвентам, соответствующим определенным размерам основных окружностей, радиусы 0ve1N1 и Ove2N2 которых находят для эквивалентной цилиндрической передачи. Параметры эквивалентной цилиндрической передачи имеют дополнительный индекс vt. Каждое из зубчатых колес такой передачи называют эквивалентным цилиндрическим зубчатым колесом с числами зубьев zvt1 и zvt2 в отличие от чисел зубьев z1 и z2 на конических колесах.
Связь между числами зубьев z1 и zvt1 или z2 и zvt2 легко установить при рассмотрении размеров концентрических окружностей конического и эквивалентного цилиндрического колес:
rvte1 = 0,5de1/cos  1 = 0,5mez1/cos
1 = 0,5mez1/cos  1 = 0,5mezvt1;
1 = 0,5mezvt1;
 |
rvte2 = 0,5de2/cos
 2 = 0,5mez1/cos
2 = 0,5mez1/cos  2 = 0,5mezvt2
2 = 0,5mezvt2
|
Внешний окружной модуль me, соответствующий расстоянию между одноименными профилями соседних зубьев по дуге концентрической окружности конического колеса на внешнем торце, равен модулю эквивалентной цилиндрической передачи. Поэтому числа зубьев zvt1и zvt2 можно выразить соотношениями:
zvt1 = z1/ cos  1 ; zvt2 = z2/ cos
1 ; zvt2 = z2/ cos  2(20.7)
2(20.7)
В общем случае числа zvt1и zvt2являются дробными и в процессе расчета не округляются, а вычисляются с точностью до 0,01.
Передаточное отношение эквивалентной цилиндрической передачи определяется следующим соотношением:
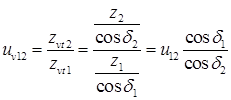 (20.8)
(20.8)
Угол зацепления 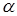 wvte эквивалентной цилиндрической передачи, радиусы ravte1 и ravte2 окружностей вершин, радиусы rfvte1 и rfvte2 окружностей впадин (рис. 20.6) рассчитывают по формулам, аналогичным выведенным ранее для цилиндрических эвольвентных передач.
wvte эквивалентной цилиндрической передачи, радиусы ravte1 и ravte2 окружностей вершин, радиусы rfvte1 и rfvte2 окружностей впадин (рис. 20.6) рассчитывают по формулам, аналогичным выведенным ранее для цилиндрических эвольвентных передач.
При расчете конических передач с криволинейной линией зуба (см. рис. 20.3) эквивалентная цилиндрическая передача является не прямозубой, а имеет винтовые зубья. Поэтому профили зубьев рассматривают в соответствующих нормальных сечениях. Прямозубое цилиндрическое зубчатое колесо, размеры и форма зубьев которого в главном сечении практически идентичны размерам и форме зубьев конического зубчатого колеса с тангенциальными и криволинейными зубьями в сечении, нормальном к средней линии зуба, называют биэквивалентным цилиндрическим колесом, число зубьев которого обозначают zvn (соответственно zvn1 и zvn2).
С достаточной для практических расчетов точностью коэффициент формы зубьев таких конических колес оценивают по аналогии с биэквивалентным цилиндрическим колесом, число зубьев которого:
zvn1 = z1/ cos  1
1 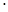 cos3
cos3 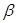 n ; zvn2 = z2/ cos
n ; zvn2 = z2/ cos  2
2 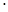 cos3
cos3 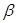 n(20.9)
n(20.9)
где 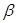 n - угол наклона средней линии зуба, соответствующий внешнему, среднему, внутреннему или другим расчетным нормальным сечениям зуба конического зубчатого колеса.
n - угол наклона средней линии зуба, соответствующий внешнему, среднему, внутреннему или другим расчетным нормальным сечениям зуба конического зубчатого колеса.
 Геометрия боковых поверхностей и профилей зубьев теснейшим образом связана с технологией изготовления конических колес. Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, ибо размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, могут использоваться только для черновой прорезки впадин или для образования впадин колес не выше 8-й степени точности.
Геометрия боковых поверхностей и профилей зубьев теснейшим образом связана с технологией изготовления конических колес. Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, ибо размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, могут использоваться только для черновой прорезки впадин или для образования впадин колес не выше 8-й степени точности.
|
Производящие колеса могут быть плоскими с  woc = 90°(рис. 20.7, а, b) или плосковершинными с
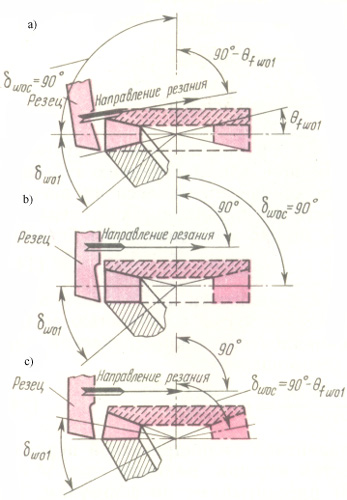
woc = 90°(рис. 20.7, а, b) или плосковершинными с  woc = 90° -
woc = 90° - 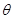 fwo1 (рис. 20.7, c) при одном и том же угле
fwo1 (рис. 20.7, c) при одном и том же угле  wo1 при вершине аксоидного конуса станочного зацепления.
wo1 при вершине аксоидного конуса станочного зацепления.
В первых двух случаях образуемые квазиэвольвентные конические колеса будут сопряженными, ибо производящие плоские колеса образуют совпадающую пару, у которой боковые производящие поверхности зубьев могут совпадать при наложении во всех своих точках (как отливка и форма или шаблон и контршаблон). Однако станок, реализующий схему станочного зацепления по рис. 20.7, а, должен иметь поворотные направляющие, допускающие установку резцовых направляющих под углом (90° - 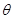 fwo1), где
fwo1), где 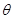 fwo1 – угол ножки зуба нарезаемого колеса в станочном зацеплении. Это усложняет конструкцию станка и используется ограниченно.
fwo1 – угол ножки зуба нарезаемого колеса в станочном зацеплении. Это усложняет конструкцию станка и используется ограниченно.
В случае движения резцов без учета угла 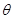 fwo1 (рис. 20.7, б) высота ножки зуба по мере приближения к вершине конуса остается неизменной, что ослабляет зуб и приводит иногда к подрезу ножки.
fwo1 (рис. 20.7, б) высота ножки зуба по мере приближения к вершине конуса остается неизменной, что ослабляет зуб и приводит иногда к подрезу ножки.
Большинство моделей станков использует плосковершинное производящее колесо, у которого вершины зубьев расположены в плоскости, а угол аксоидного конуса в станочном зацеплении рассчитывается с учетом угла 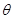 fwo1 ножки зуба нарезаемого колеса. Два плосковершинных колеса не образуют совпадающую производящую пару, и поэтому нарезаемые квазиэвольвентные колеса будут несопряженными. Эти погрешности обычно являются незначительными и ими обычно пренебрегают.
fwo1 ножки зуба нарезаемого колеса. Два плосковершинных колеса не образуют совпадающую производящую пару, и поэтому нарезаемые квазиэвольвентные колеса будут несопряженными. Эти погрешности обычно являются незначительными и ими обычно пренебрегают.
|
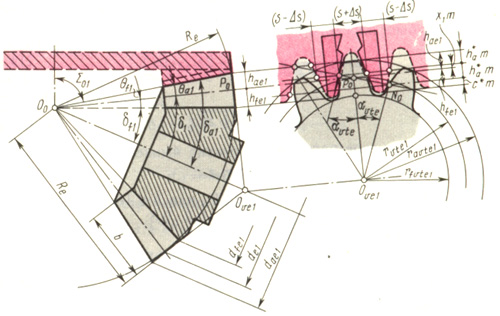
Расчетная схема, приведенная на рис. 20.8, позволяет на базе станочного зацепления конического колеса с производящим плосковершинным колесом перейти к эквивалентному станочному зацеплению с теоретическим исходным контуром. Исходный контур, совпадающий с реечным контуром, принятым в качестве базового для определения теоретических форм и размеров зубьев конических колес, регламентирован по ряду параметров: 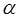 = 20°; h*a = 1,2 ; c* = 0,2 ;
= 20°; h*a = 1,2 ; c* = 0,2 ; 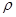
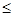 0,3. Однако с учетом особенностей методов нарезания зубьев эти параметры можно изменять в пределах использования стандартного инструмента. Так, например, можно допускать неравенство толщины зуба и ширины впадины по делительной прямой за счет относительного расположения соседних резцов; не требуется строгого соответствия номинального модуля резцов модулю нарезаемого колеса. Внешний модуль может быть нестандартным и даже дробным. Можно изменять угол
0,3. Однако с учетом особенностей методов нарезания зубьев эти параметры можно изменять в пределах использования стандартного инструмента. Так, например, можно допускать неравенство толщины зуба и ширины впадины по делительной прямой за счет относительного расположения соседних резцов; не требуется строгого соответствия номинального модуля резцов модулю нарезаемого колеса. Внешний модуль может быть нестандартным и даже дробным. Можно изменять угол 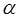 за счет наклона резцов,
за счет наклона резцов,
Расчет параметров конической передачи проводят а такой последовательности (рис. 20.8):
число зубьев плоского колеса:
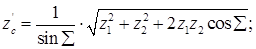 (20.10)
(20.10)
при 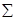 =90°
=90°
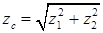 (20.11)
(20.11)
внешнее конусное расстояние:
Re = 0,5mezc(20.12)
ширина зубчатого венца b 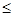 0,3Re или b
0,3Re или b 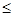 10me ; коэффициент ширины зубчатого венца kbe = b/Rwe = 0,2
10me ; коэффициент ширины зубчатого венца kbe = b/Rwe = 0,2 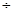 0,3 ;
0,3 ;
угол делительного конуса
 1 = arctg ( sin
1 = arctg ( sin 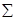 /(z2/z1 + cos
/(z2/z1 + cos 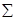 )) ; (20.13)
)) ; (20.13)
 2 =
2 = 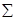 -
-  1 ;(20.14)
1 ;(20.14)
при 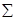 =90°
=90°
 1 = arctg ( z1/z2 ); (20.15)
1 = arctg ( z1/z2 ); (20.15)
коэффициент смещения исходного контура x1 = 0 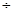 0,6в зависи-мости от числа зубьев z1 и передаточного отношения передачи ; x2 = - x1;
0,6в зависи-мости от числа зубьев z1 и передаточного отношения передачи ; x2 = - x1;
x1 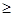 x1min = 1,068 – 0,058z1/cos
x1min = 1,068 – 0,058z1/cos  1 (20.16)
1 (20.16)
коэффициент изменения расчётной толщины зуба исходного контура
x 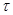 1 = 0,03 - 0,008(z2/z1 – 2,5) ; x
1 = 0,03 - 0,008(z2/z1 – 2,5) ; x 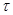 2 = - x
2 = - x 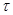 1 (20.17)
1 (20.17)
Расчёт параметров зубчатых колёс проводят по следующим расчётным формулам, вывод которых основан на расчётной схеме (рис 20.8)
внешняя высота головки зуба
hae1 = (h*a + x1)me ; hae2 = 2h*ame – hae1;(20.18)
внешняя высота ножки зуба
hfe1= hae2 + c*me ; hfe2 = hae1 + c*me ; (20.19)
внешняя высота зуба
he = hae + hfe;(20.20)
внешняя окружная толщина зуба
se1 = (0,5 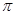 + 2x1tg
+ 2x1tg 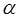 + x
+ x 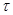 1)me ; se2 =
1)me ; se2 = 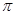 me – se1 ; (20.21)
me – se1 ; (20.21)
угол ножки зуба
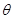 f1 = arctg hfe1/Re ; (20.22)
f1 = arctg hfe1/Re ; (20.22)
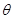 f2 = arctg hfe2/Re ; (20.23)
f2 = arctg hfe2/Re ; (20.23)
угол головки зуба
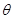 1 <
1 < 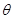 f2 ;
f2 ; 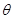 a2 <
a2 < 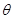 f1 (20.24)
f1 (20.24)
угол конуса вершин
 a1 =
a1 =  1 +
1 + 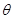 a1 ;
a1 ;  a2 =
a2 =  2 +
2 + 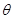 a2 (20.25)
a2 (20.25)
угол конуса впадин
 f1 =
f1 =  1 +
1 + 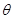 f1 ;
f1 ;  f2 =
f2 =  2 +
2 + 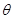 f2 (20.26)
f2 (20.26)
внешний делительный диаметр
de1 = mez1 ; de2 = mez2 (20.27)
внешний диаметр вершин зубьев
dae1 = de1 + 2hae1 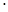 cos
cos  1 ; dae2 = de2 + 2hae2
1 ; dae2 = de2 + 2hae2 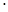 cos
cos 2 (20.28)
2 (20.28)
При выборе исходных данных учитывают заданные передаточные отношения u12 и его допустимое отклонение в связи с тем, что число зубьев – целые числа.
Рекомендуется назначать числа зубьев колёс в пределах от 12 до 100.
Для прямозубых конических передач передаточные отношения рекомендуется назначать: u12 < 5– для редуктора,u12 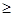 0,35– для мультипликатора.
0,35– для мультипликатора.
Параметры исходного контура – по ГОСТ 13754-81
Контрольные вопросы к лекции N20.
1. Для каких целей используются конические зубчатые передачи?
2. Укажите достоинства и недостатки конических зубчатых передач
3. Каковы особенности расчёта геометрии конических колёс и передач?
4. Расскажите об особенностях технологии зуборезания конических колёс
5. Как определяются углы вершин начальных конусов в конической прямозубой передаче при известном передаточном отношении и межосевом угле?
| <== предыдущая лекция | | | следующая лекция ==> |
| Волновые зубчатые передачи | | | Гилерболоидные зубчатые передачи. |
Дата добавления: 2017-02-13; просмотров: 5175;











