Силовой расчет механизмов.
При проектировании механизмов машин (их звеньев и кинематических пар) приходится решать задачи обеспечения необходимой прочности, жесткости и долговечности. Для этого необходимо знать силовую нагрузку звеньев и кинематических пар.
При решении задач силового расчета механизмов закон движения ведущего звена предполагается заданным; точно также предполагаются известными массы и моменты инерции звеньев механизма. Таким образом, всегда могут быть определены те силы инерции, которые необходимы для решения задач силового расчета с использованием уравнений равновесия.
В тех случаях, когда при расчете в число заданных сил не входят силы инерции звеньев, расчет называется статическим. Если в число заданных (или определенных) сил при расчете входят и силы инерции звеньев, то такой расчет называется кинетостатическим.
Так как метод расчета для обоих случаев является общим, то в дальнейшем будем предполагать, что в число заданных сил входят и силы инерции, известные нам по величине, направлению и точкам приложения.
В первом приближении будем вести расчет без учета сил трения.
Механизм машинного агрегата обычно является многозвенной системой, нагруженной силами и моментами, приложенными к различным ее звеньям. Чтобы лучше себе ее представить рассмотрим силовую компрессорную установку с приводом от асинхронного электродвигателя (см. рис. 9.1).
К поршню приложены сила сопротивления воздуха, к ротору электродвигателя – движущий момент. Если компрессор многоцилиндровый, то на каждый поршень будет действовать сила сопротивления и картина нагружения станет более сложной.
Так как в курсе “Теоретическая механики” и на упражнении мы разбирали пример по определению усилий в кинематических парах рычажного механизма без учёта трения и на нем были сформулированы основные положения метода кинетостатики и последовательность решения задачи об определении усилий в кинематических парах, то сейчас лишь кратко сформулируем задачи силового расчёта.
Силовой расчет механизмов основывается на решении прямой (первой) задачи динамики по заданному закону движения определить действующие силы.
1. Закон движения начальных (или начального при W = 1) звеньев считается заданным.
2. Внешние силы, приложенные к звеньям механизма, считаются заданными.
3. Подлежат определению только реакции в кинематических парах.
Иногда внешние силы, приложенные к начальным звеньям считают неизвестными, тогда в силовой анализ входит определение таких величин этих сил, при которых выполняются принятые законы движения начальных звеньев.
При решении обеих задач используется принцип Д’Аламбера, согласно которому звено механизма может рассматриваться как находящееся в равновесии, если ко всем внешним силам, действующим на него добавить силы инерции.
Учет ускоренного движения звеньев выполним методом кинетостатики, условно приложив к каждому подвижному звену механизма главный вектор 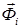 и главный момент
и главный момент 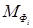 сил инерции. Тогда для каждого звена можно записать три уравнения:
сил инерции. Тогда для каждого звена можно записать три уравнения:
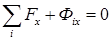 (9.1)
(9.1)
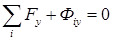 (9.2)
(9.2)
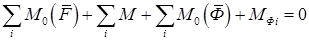 (9.3)
(9.3)
Уравнения равновесия звеньев в этом случае называются уравнениями кинетостатики.
Два алгебраических уравнения (9.1) и (9.2) могут быть заменены одним эквивалентным векторным уравнением сил:
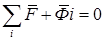
Главный вектор 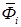 , и главный момент
, и главный момент 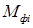 сил инерции звена i определяются по уравнениям
сил инерции звена i определяются по уравнениям
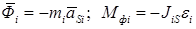 (9.4)
(9.4)
Уравнение 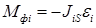 предполагает, что главный вектор сил инерции
предполагает, что главный вектор сил инерции 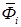 приложен к центру масс
приложен к центру масс 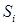 .
.
Следует подчеркнуть, что никакой силы 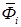 , и никакой пары сил
, и никакой пары сил 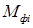 , к звену i в действительности не приложено. Главный вектор
, к звену i в действительности не приложено. Главный вектор 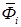 , и главный момент
, и главный момент 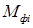 сил инерции не имеют никакого физического содержания и в расчетных уравнениях (9.l) — (9.3) выполняют роль не более чем чисто математических величин, посредством которых учитывается влияние ускоренного движения звеньев.
сил инерции не имеют никакого физического содержания и в расчетных уравнениях (9.l) — (9.3) выполняют роль не более чем чисто математических величин, посредством которых учитывается влияние ускоренного движения звеньев.
Силы в кинематических парах, являющиеся искомыми, определяют из уравнений (9.1) - (9.3), в которых они содержатся в составе сумм 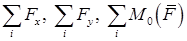 . Поскольку значения
. Поскольку значения 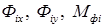 зависят от ускорений, искомые силы также зависят от ускорений. Следовательно, для проведения силового расчета надо знать закон движения механизма.
зависят от ускорений, искомые силы также зависят от ускорений. Следовательно, для проведения силового расчета надо знать закон движения механизма.
|
 |
Рассмотрим действие сил в кинематических парах, считая, что влияние трения мало и им можно пренебречь.
Сила взаимодействия звеньев, образующих низшую пару, представляет собой равнодействующую элементарных сил, распределенных по поверхности соприкосновения звеньев. Как известно из теоретической механики, сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности.
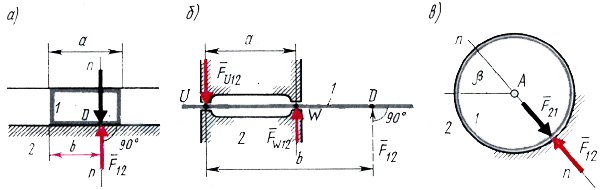
В поступательной паре сила 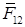 , приложенная к звену 1 от звена 2, направлена по нормали n – n (рис 9.2, а). Модуль силы
, приложенная к звену 1 от звена 2, направлена по нормали n – n (рис 9.2, а). Модуль силы 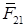 и расстояние b неизвестны и должны быть определены в процессе силового расчета. Сказанное полностью относится и к силе
и расстояние b неизвестны и должны быть определены в процессе силового расчета. Сказанное полностью относится и к силе 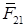 , приложенной к звену 2 от звена 1, так как силы взаимодействия
, приложенной к звену 2 от звена 1, так как силы взаимодействия 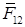 и
и 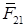 , связаны третьим законом Ньютона:
, связаны третьим законом Ньютона: 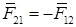
При выполнении силового расчета расстояние b может получиться больше длины а (рис. 9.2, б). Это означает, что к звену 1 приложена уже не одна, а две реакции: 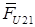 и
и 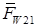 - направленные навстречу друг другу и неизвестные по модулю. Именно они и представляют реальное силовое воздействие на стержень 1 от звена 2, а вектор
- направленные навстречу друг другу и неизвестные по модулю. Именно они и представляют реальное силовое воздействие на стержень 1 от звена 2, а вектор 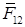 , полученный формально из уравнений (показан на рис. 9.2, б штрихами), является лишь их равнодействующей.
, полученный формально из уравнений (показан на рис. 9.2, б штрихами), является лишь их равнодействующей.
Таким образом, поступательная пара в любом случае (рис. 9.2, а, б) вносит в расчетные уравнения две неизвестные величины.
Во вращательной паре сила 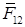 направлена нормально к цилиндрической поверхности соприкосновения обоих звеньев, т. е. проходит через центр шарнира А (рис. 9.2, в). Положение центра шарнира всегда известно, но модуль силы
направлена нормально к цилиндрической поверхности соприкосновения обоих звеньев, т. е. проходит через центр шарнира А (рис. 9.2, в). Положение центра шарнира всегда известно, но модуль силы 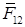 и угол
и угол 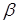 неизвестны. И эта низшая пара приносит в расчет две неизвестные.
неизвестны. И эта низшая пара приносит в расчет две неизвестные.
Следовательно, от каждой силы, действующей в любой низшей кинематической паре, в расчетных уравнениях (9.1) - (9.3) появляются две неизвестные величины.
Пусть вращательная пара конструктивно выполнена в виде двух подшипников: О' и О" (рис. 9.3). Сила 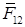 , полученная из расчета, расположена (во взятом примере) в плоскости ВВ зубчатой передачи и является равнодействующей реакций
, полученная из расчета, расположена (во взятом примере) в плоскости ВВ зубчатой передачи и является равнодействующей реакций 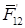 и
и 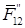 . Эти реакции и представляют собой
. Эти реакции и представляют собой
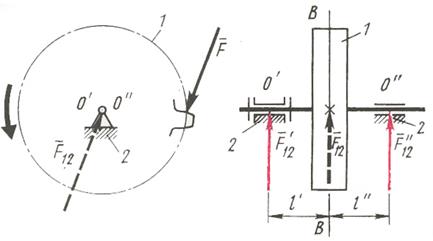 |
реальное силовое нагружение подшипников. Именно они нужны для расчета
|
В высшей паре контакт звеньев может быть либо точечным, либо линейным. Силовое взаимодействие звеньев при точечном контакте выражается в виде сосредоточенной силы, при линейном - в виде нагрузки, распределенной по линии контакта. В последнем случае под силой взаимодействия понимают равнодействующую элементарных распределенных сил.
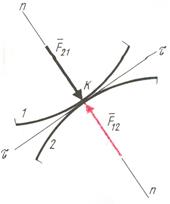 Сила
Сила 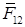 в высшей паре направлена по общей нормали п - п (рис. 9.4).Следовательно, для силы
в высшей паре направлена по общей нормали п - п (рис. 9.4).Следовательно, для силы 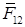 известны как точка приложения (точка К), так и линия действия и неизвестным остается только модуль. Таким образом, в расчетных уравнениях (9.1) - (9.3) члены, образованные силами взаимодействия в высших парах, содержат по одному неизвестному.
известны как точка приложения (точка К), так и линия действия и неизвестным остается только модуль. Таким образом, в расчетных уравнениях (9.1) - (9.3) члены, образованные силами взаимодействия в высших парах, содержат по одному неизвестному.
|
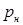 низших и
низших и 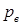 высших кинематических пар. Так как для каждого звена механизма можно записать три расчетных уравнения (9.1) – (9.3), то общее число уравнений для всех его п подвижных звеньев составит
высших кинематических пар. Так как для каждого звена механизма можно записать три расчетных уравнения (9.1) – (9.3), то общее число уравнений для всех его п подвижных звеньев составит 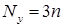
Для плоской схемы механизма число неизвестных, определяемых из какой-либо системы уравнений 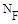 =
= 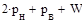 , должно совпадать с числом уравнений
, должно совпадать с числом уравнений 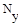 = 3n, т.е.
= 3n, т.е. 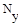 =
= 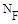 или
или
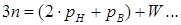 (9.4)
(9.4)
Для структурной группы Ассура число уравнений кинетостатики 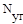 = 3n, число неизвестных -
= 3n, число неизвестных - 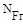 =
= 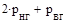 , где
, где
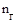 - число подвижных звеньев группы Ассура,
- число подвижных звеньев группы Ассура,
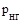 - число низших кинематических пар группы,
- число низших кинематических пар группы,
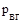 - число высших кинематических пар группы.
- число высших кинематических пар группы.
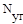 =
= 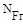
Дата добавления: 2017-02-13; просмотров: 2239;











