Динамика механизмов.

Задачи динамики:

1. Прямая задача динамики (силовой анализ механизма) – по за данному закону движения определить действующие на его звенья силы, а также реакции в кинематических парах механизма.

2. Обратная задача динамики – по заданным силам, приложенным к механизму, определить истинный закон движения механизма.

В динамический анализ механизмов могут быть включены и задачи уравновешивания и виброзащиты.

Давайте вначале займемся решением обратной задачи динамики, считая все звенья механизмов жесткими.

К механизму машинного агрегата во время его движения приложены различные силы. Это движущие силы, силы сопротивления (иногда их называют силами полезного сопротивления), силы тяжести, силы трения и многие другие силы. Характер их действия может быть различным:

а) некоторые зависят от положения звеньев механизма;

б) некоторые от изменения их скорости;

в) некоторые постоянны.

Своим действием приложенные силы сообщают механизму тот или иной закон движения.

Силы, действующие в машинах, и их характеристики

Силы и пары сил (моменты), приложенные к меха­низму машины, можно разделить на следующие группы.

1. Движущие силы и моменты, совершающие по­ложительнуюработу за время своего действия или за один цикл, если они изменяются периодически. Эти силы и моменты приложены к звеньям механизма, которые называются ведущими.

2. Силы и моменты сопротивления, совершающие отрицательнуюработу за время своего действия или за один цикл. Эти силы и моменты делятся, во-первых, на силы и моменты полезного сопротивления, которые совершают требуемую от машины работу и приложены к звеньям, называемым ведомыми, и, во-вторых, на силы и моменты сопротивления среды (газа, жидкости), в которой движутся звенья механизма. Силы сопротивления среды обычно малы по срав­нению с другими силами, поэтому в дальнейшем они учитываться не будут, а силы и моменты полезного сопротивления будут называться просто силами и моментами сопротивления.

3. Силы тяжести подвижных звеньев и силы упру­гости пружин. На отдельных участках движения механизма эти силы могут совершать как положительную, так и отрицательную ра­боту. Однако за полный кинематический цикл работа этих сил равна нулю, так как точки их приложения движутся циклически.

4. Силы и моменты, приложенные к корпусу машины (т. е. к стойке) извне. К ним помимо силы тяжести корпуса относятся реакция основания (фундамента) машины на ее корпус и многие другие силы. Все эти силы и моменты, поскольку они приложены к неподвижному корпусу (стойке), работы не совершают.

5. Силы взаимодействия между звеньями ме­ханизма, т. е. силы, действующие в его кинематических парах. Эти силы согласно 3-му закону Ньютона всегда взаимообратны. Их нормальные составляющие работы несовершают, а касательные со­ставляющие, т. е. силы трения, работу совершают, причем работа силы трения на относительном перемещении звеньев кинематической пары отрицательна.

Силы и моменты первых трех групп относятся к категории актив­ных. Обычно они известны или могут быть оценены. Все эти силы и моменты приложены к механизму извне, а поэтому являются внешними. К числу внешних относятся также и все силы и моменты 4-й группы. Однако не все они являются активными.

	Рис. 6.1		Рис. 6.2

Силы 5-й группы, если рассматривать механизм в целом, не вы­деляя отдельных его частей, являются внутренними. Эти силы пред­ставляют собой реакции на действие активных сил. Реакцией будет также и сила (или момент), с которой основание (фундамент) маши­ны действует на ее корпус (т. е. на стойку механизма). Реакции напе­ред неизвестны. Они зависят от активных сил и моментов и от ускоре­ний звеньев механизма.

Наибольшее влияние на закон движения механизма оказывают движущие силы и моменты, а также силы и моменты сопротивления. Их физическая природа, величина и характер действия определя­ются рабочим процессом машины или прибора, в которых исполь­зован рассматриваемый механизм. В большинстве случаев эти силы и моменты не остаются постоянными, а изменяют свою величину при изменении положения звеньев механизма или их скорости. Эти функциональные зависимости, представленные графически, или мас­сивом чисел, или аналитически, носят название механических характеристик и при решении задач считаются известными.

При изображении механических характеристик будем придержи­ваться следующего правила знаков: силу и момент будем считать положительными, если на рассматриваемом участке пути (линейном или угловом) они производят положительную работу.

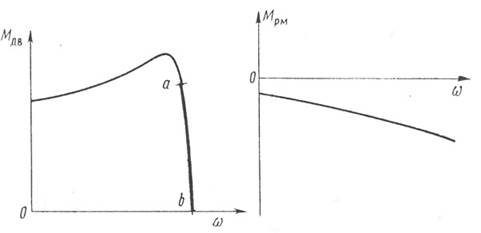
Характеристики сил, зависящих от скорости.На рис. 6.1 пока­зана механическая характеристика асинхронного электродвига­теля — зависимость движущего момента от угловой скорости ротора машины. Рабочей частью характеристики является участок ab, на котором движущий момент резко уменьшается даже при незначитель­ном увеличении скорости вращения.

От скорости зависят силы и моменты, действующие также в таких роторных машинах, как электрогенераторы, вентиляторы, воздухо­дувки, центробежные насосы (рис. 6.2) и многие другие.

Рис 6.3

При увеличении скорости момент двигателей обычно уменьша­ется, а момент машин-потребителей механической энергии обычно увеличивается. Такое свойство очень полезно, так как автоматиче­ски содействует устойчивому поддержанию режима движения ма­шины, и чем сильнее оно выражено, тем устойчивость больше. Назо­вем такое свойство машин саморегулированием.

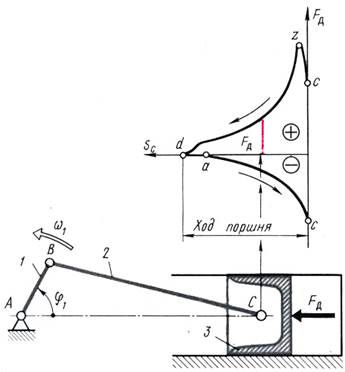
Характеристики сил, зависящих от перемещения.На рис.6.3пока­зана кинематическая схема механизма двухтактного двигателя внут­реннего сгорания (ДВС) и его механическая характеристика. Сила 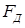, приложенная к поршню 3, действует всегда влево. Поэтому при движении поршня влево (процесс расширения газов) она совершает положительную работу и показана со знаком плюс (ветвь czd). При движении поршня вправо (процесс сжатия газов) сила 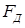получает знак минус (ветвь dac). Если подача топлива в ДВС не изменяется, то при следующем обороте начального звена (звено 1) механическая характеристика 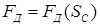повторит свою форму. Это значит, что сила 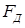будет изменяться периодически.

Работа силы 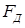графически изобразится площадью, ограничен­ной кривой 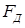(s_c). На рис.6.3 эта площадь имеет две части: положи­тельную и отрицательную, причем первая больше второй. Поэтому работа силы 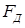за полный период будет положительной. Следова­тельно, сила 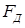является движущей, хотя она и знакопеременна. Отметим попутно, что если сила, будучи знакопеременной, совершает за один период отрицательную работу, то она является силой сопро­тивления.

Рис. 6.4

Силы, зависящие только от перемещения, действуют во многих других машинах и приборах (в поршневых компрессорах, ковочных ма­шинах, строгальных и дол­бежных станках, разнооб­разных приборах как с пневмоприводом, так и с пру­жинными двигателями и т. д.), причем действие сил 6 может быть как периодическим, так и непериодическим.

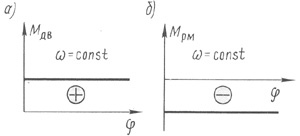
Вместе с тем нужно отметить, что момент машин роторного типа от перемещения, т. е. от угла поворота ротора не зависит; характе­ристики таких машин при 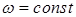изображены на рис.6.4, а, б. При этом у машин-двигателей 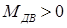, а у машин-потребителей механи­ческой энергии (т.е. рабочих машин) .

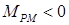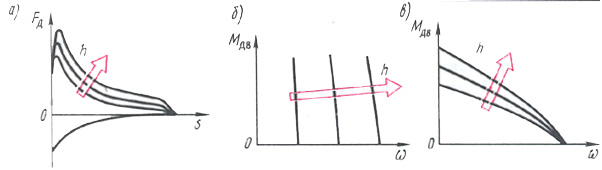
Если изменять подачу топлива в ДВС, то его механическая харак­теристика примет вид семейства кривых (рис.6.5, а): чем больше подача топлива (параметр h семейства), тем выше располагается характеристика. Семейством кривых изображается и механическая характеристика шунтового электродвигателя (рис. 6.5, б): чем боль­ше сопротивление цепи обмотки возбуждения двигателя (пара­метр h), тем правее размещается кривая. Характеристика гидродина­мической муфты также имеет вид семейства кривых (рис.6.5, в): чем больше наполнение муфты жидкостью (параметр h), тем правее и выше располагаются характеристики.

Таким образом, воздействуя на параметр h, можно управлять режимом работы привода — теплового, электрического или гидрав­лического, увеличивая его движущую силу или скорость. Вместе с тем параметр управления h связан с величиной потока энергии, протекающей через машину, т. е. определяет ее нагруженность и производительность.

	Рис. 6.5

Рис. 6.6

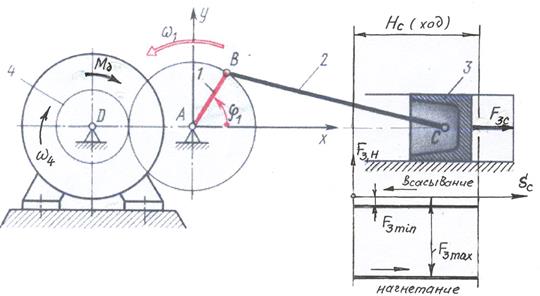Механизм машинного агрегата обычно является многозвенной системой, нагруженной силами и моментами, приложенными к различным ее звенья. Чтобы лучше ее себе представить, рассмотрим силовую насосную установку с приводом от асинхронного электродвигателя.

К поршню 3 приложена сила сопротивления жидкости, к ротору 4 электродвигателя – движущий момент. Если насос многоцилиндровый, то на каждый поршень будет действовать сила сопротивления, так что картина нагружения станет более сложной.

Для определения закона движения механизма под действием заданных внешних (активных) сил необходимо решить уравнение его движения. Основой для составления уравнения движения служит теорема об изменении кинетической энергии механизма с W=1, которая формулируется так:

Изменение кинетической энергии механизма происходит за счет работы всех сил и моментов, приложенных к механизму

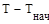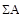= (6.1)

В плоском механизме звенья совершают вращательные, поступательные и плоскопараллельные движения, тогда кинематическая энергия механизма

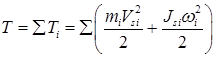(6.2)

для всех подвижных звеньев механизма

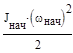= (6.3)