Динамическая модель
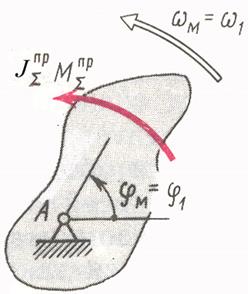 Положение механизма с W=1 вполне определяется одной координатой, которая называется обобщенной координатой. В качестве обобщенной координаты чаще всего принимают угловую координату звена, совершающего вращательное движение. В этом случае динамическая модель будет представлена в виде:
Положение механизма с W=1 вполне определяется одной координатой, которая называется обобщенной координатой. В качестве обобщенной координаты чаще всего принимают угловую координату звена, совершающего вращательное движение. В этом случае динамическая модель будет представлена в виде:
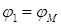 - обобщенная угловая координата модели
- обобщенная угловая координата модели
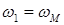 - угловая скорость модели
- угловая скорость модели
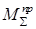 - суммарный приведенный момент (обобщенная сила - эквивалент всей заданной нагрузки, приложенной к механизму)
- суммарный приведенный момент (обобщенная сила - эквивалент всей заданной нагрузки, приложенной к механизму)
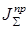 - суммарный приведенный момент инерции, являющийся эквивалентом инерционности механизма.
- суммарный приведенный момент инерции, являющийся эквивалентом инерционности механизма.
В случае приведения, фактически действующие силы и моменты заменяем суммарным приведенным моментом, приложенным к динамической модели.
Следует подчеркнуть, что сделанная замена не должна нарушить закона движения механизма, определяемого действием фактически приложенных сил и моментов.
В основу приведения сил и моментов должно быть положено условие равенства элементарных работ, т.е. элементарная работа каждой силы на возможном перемещении точки ее приложения или момента на возможном угловом перемещении того звена, на котором он действует должна быть равна элементарной работе приведенного момента на возможном угловом перемещении динамической модели.
Рассмотрим в качестве примера приведение сил и моментов, приложенных к звеньям машинного агрегата (рис. 6.6) , назначив в качестве обобщенной координаты угловую координату 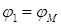 .
.
Определим 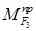 , заменяющий приложенную силу
, заменяющий приложенную силу 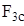 . По условию равенства элементарных работ
. По условию равенства элементарных работ
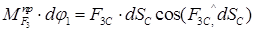
решив относительно искомой величины 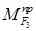 и разделив возможные перемещения на время, получим
и разделив возможные перемещения на время, получим
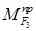 =
= 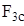
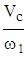 cos(
cos( 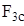 ,
, 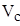 ), где cos(
), где cos( 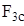

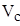 )=
)= 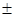 1
1
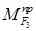 =
= 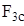
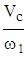 =
= 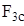
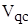 =
= 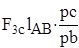 , где
, где 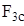
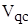 для решения на ЭВМ,
для решения на ЭВМ,
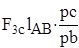 с использованием
с использованием 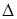 скоростей.
скоростей.
Аналогично произведем приведение к динамической модели (звену 1) сил 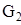 ,
, 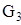 , и
, и 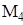 .
.
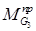 =
= 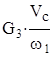 cos(
cos( 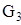 ,
, 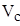 ) = 0 ,0 т.к. cos(
) = 0 ,0 т.к. cos( 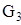 ,
, 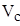 ) = 0.
) = 0.
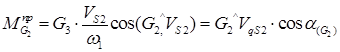 =
=
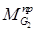 =
= 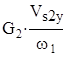 =
= 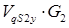
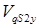 - проекция скорости центра масс
- проекция скорости центра масс  на ось у.
на ось у.
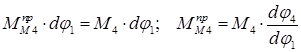
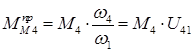
Подобным же образом найдем 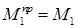 .
.
Если алгебраически сложить все приведенные моменты, приложенные к начальному звену, то получим суммарный приведенный момент, который заменяет собой все силы и моменты, действующие на механизм.
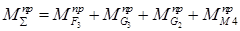 (6.5)
(6.5)
Приведение масс.
Приведение масс делают с той же целью, что и приведение сил:
видоизменить и упростить динамическую схему механизма, т.е. прийти к соответствующей динамической модели, а, следовательно, и упростить решение уравнения движения.
Если в качестве динамической модели принято начальное звено с обобщенной координатой 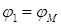 , то кинетическая энергия модели должна быть равна сумме кинетических энергий всех звеньев механизма, т.е. в основу приведения масс к начальному звену положено условие равенства кинетических энергий.
, то кинетическая энергия модели должна быть равна сумме кинетических энергий всех звеньев механизма, т.е. в основу приведения масс к начальному звену положено условие равенства кинетических энергий.
Приведенным моментом инерции называется параметр динамической модели, кинетическая энергия которой равна сумме кинетических энергий реально движущихся звеньев.
Запишем условие равенства кинетической энергии отдельного взятого звена, всего механизма и модели для отдельного звена: 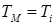
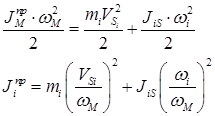 (6.6)
(6.6)
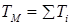
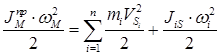
где 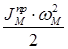 для модели,
для модели, 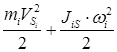 для реальных звеньев механизма
для реальных звеньев механизма
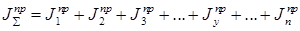
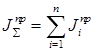 (6.7)
(6.7)
Передаточные функции в скобках не зависят от 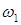 , поэтому
, поэтому 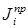 может быть определен далее в том случае, если закон движения модели (начального звена) неизвестен. При
может быть определен далее в том случае, если закон движения модели (начального звена) неизвестен. При 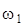 =
= 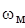
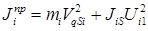 , где
, где 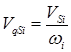 ,
, 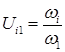
Давайте определим приведенные моменты инерции 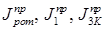
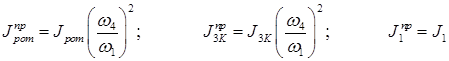
Все эти моменты инерции не зависят от углового положения начального звена. Эта группа звеньев, связанных с динамической моделью линейными передаточными отношениями называется звеньями первой группы, а их моменты инерции – моментами инерции первой группы.
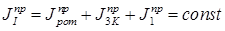
Определим моменты инерции 2-го и 3-го звеньев
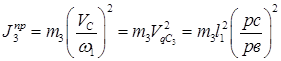
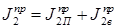
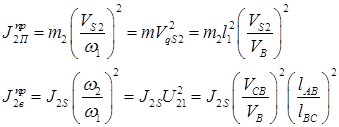
Моменты инерции первой и второй группы звеньев и суммарный приведенный момент инерции рассматриваемой установки показан на рис. 6.7
|
Контрольные вопросы к лекции N6
1. Сформулируйте определение прямой и обратной задач динамики.
2. Что понимается над динамической моделью механизма?
3. С какой целью производится приведение сил и моментов в механизме? Какое условие положено в основу приведения сил и моментов?
4. Какое условие положено в основу замены масс и моментов инерции при приведении?
5. Напишите формулу кинетической энергии для кривошипно-ползунного механизма.
Дата добавления: 2017-02-13; просмотров: 1857;











