Классификация структурных групп.
Анализ (3.6),..., (3.10) показывает, что в машинах и механизмах имеется большое количество разнообразных структурных групп. Это усложняет их анализ и синтез. С целью упрощения изучения и анализа группы Ассура пытаются классифицировать.
В настоящее время нет единой классификации всех структурных групп. Наиболее полно проклассифицированы только группы Accура, существующие в трехмерном трёхподвижном пространстве, допускающем два независимых поступательных движения вдоль осей Х и Y и одно вращательное вокруг оси Z. Отметим, что в современном машиностроении именно механизмы, существующие в трехмерном трехподвижном пространстве, нашли самое широкое распространение на практике. Потому в данной лекции рассмотрим структурную классификацию структурных групп и так называемых плоских механизмов.
Напомним, что механизмы с высшими парами можно привести к механизмам с низшими кинематическими парами. В настоящее время признано, что лучшей классификацией механизмов с низшими кинематическими парами, которые существуют в трехмерном трехподвижном пространстве, является структурная классификация Ассура-Артоболевского [3]. Достоинством этой классификации является то, что с ее помощью не только упрощаются структурный анализ и синтез механизмов, но и она увязывается с методами кинематического, силового и динамического исследования механизмов.
Каждый рычажный механизм рассматривается как система, состоящая из элементарного первичного механизма, который в классификации Ассура-Артоболевского назван механизмом 1 класса, и соединенных с ним и между собой структурных групп.
Все механизмы и структурные группы, в них входящие, делятся на классы, а класс механизма в целом определяется высшим классом структурной группы, которая в него входит.
Элементарные механизмы условно отнесены к механизмам 1 класса.
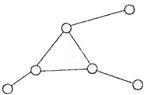
Класс структурной группы определяется числом кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами.
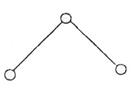
При этом двухповодковая структурная группа (рис.3.3, а), не имеющая замкнутого контура, отнесена ко второму классу (см. табл. 3.1)
Порядок группы определяется числом внешних кинематических пар.
Так как на практике наибольшее применение нашла двухповодковая группа, то, в зависимости от места размещения на ней вращательных и поступательных кинематических пар, эта группа разделяется еще и по видам (рис.3.11).
| N п/п | Структурная схема | Класс группы | Порядок группы | Вид группы |
| II | I | ||
| III | - | ||
| IV | - |
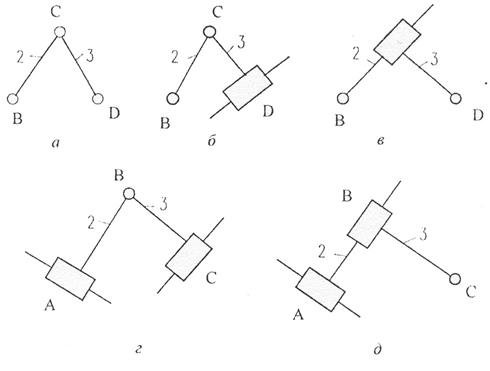 |
Рис. 3.11 Виды двухповодковых структурных групп:
а – диада 1 вида; б – диада 2 вида; в – диада 3 вида; г – диада 4 вида; д – диада 5 вида
К первому виду отнесена диада, у которой все кинематические пары - вращательные (рис. 3.11, а). Диада, у которой одна из внешних кинематических пар является поступательной, отнесена ко второму виду (рис. 3.11, 6). Диада, у которой внутренняя пара поступательная, относится к третьему виду (рис. 3.11, в). Двухповодковая группа, у которой две внешние кинематические пары поступательные, отнесена к четвертому виду (рис. 3.11, г). И, наконец, группа, у которой одна внешняя и внутренняя пары - поступательные, отнесена к пятому виду (рис. 3.11, д).
Казалось бы, что идя по пути последовательной замены в диаде Сильвестера вращательных кинематических пар поступательными, можно заменить все три вращательные пары на поступательные. Однако этого делать нельзя, так как в этом случае получим не структурную группу, а клиновой, который, конечно же, не является структурной группой и даже существует в другом по подвижности пространстве.
При проектировании механизмов без избыточных связей чаще всего применяется метод наслоения групп, предложенный Л.В. Ассуром. При этом механизм образуется из первичного механизма (обычно кривошип со стойкой) и присоединённых к нему групп нулевой подвижности. Что бы избежать избыточных связей, необходимо, что бы они отсутствовали как в первичном механизме так и в присоединяемых группах. При структурном синтезе механизма без избыточных связей с W=1 (в частном случае) необходимо соблюдать правила:
· Замкнутая кинематическая цепь механизма с W=1 и одним контуром без избыточных связей (q=0) должна иметь такой набор кинематических пар, что бы сумма их подвижностей была равна семи (7) для пространственного механизма и четырём (4) для плоского.
· Последующие присоединяемые группы звеньев, образующий после присоединения замкнутый контур, должны иметь в своём составе набор кинематических пар, сумма подвижностей которого равна 6 для пространственного механизма и 3 для плоского.
Давайте разберем несколько примеров структурного анализа.
1. Дано: 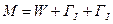
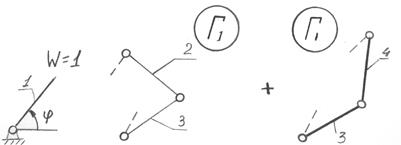

2. Дано: 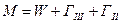
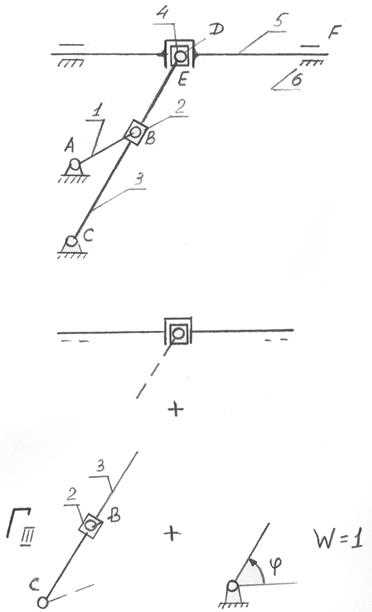
Структурный анализ – задача обратная синтезу. Структурный анализ заданного механизма следует производить путём расчленения его на структурные группы и первичные механизмы в порядке обратном образованию механизма.
От структурной схемы механизма при этом отделяют по одной все структурные группы таким образом, что бы оставшаяся цепь продолжала быть механизмом. После снятия всех групп далжны остаться первичные механизмы, количество которых определяет число степеней свободы механизма
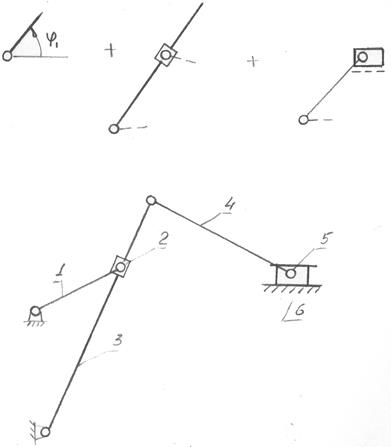
3. Дано: Поперечно-строгальный станок.
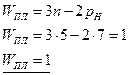
Дата добавления: 2017-02-13; просмотров: 3690;











