Структурный синтез простых и сложных механизмов с помощью структурных групп.
Наиболее распространенным методом создания механизмов с замкнутыми кинематическими цепями в настоящее время является метод присоединения к элементарным механизмам структурных групп или групп Accypa. Этот метод образования механизмов впервые был предложен Л.В. Ассуром для так называемых плоских замкнутых цепей, заканчивающихся -во всех направлениях поводками с вращательными или поступательными кинематическими парами.
Кинематические цепи, обладающие нулевой подвижностью относительно внешних кинематических пар и не распадающиеся на более простые цепи, удовлетворяющие этому условию, получили название структурных групп или групп Ассура.
Структурную формулу любого простого или сложного механизма. образованного с помощью структурных групп, можно представить следующим образом:
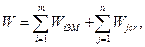 (3.1)
(3.1)
где W - подвижность синтезируемого механизма; 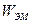 - подвижность элементарного механизма;
- подвижность элементарного механизма; 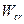 - подвижность структурной группы; m - число элементарных первичных механизмов; n - число присоединяемых структурных групп; i=1, 2, ... m; j =1, 2, ... n.
- подвижность структурной группы; m - число элементарных первичных механизмов; n - число присоединяемых структурных групп; i=1, 2, ... m; j =1, 2, ... n.
Так как подвижность присоединяемых (ой) структурных(ой) групп(ы) равна нулю, то 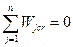 , а значит, (3.1) эквивалентно выражению:
, а значит, (3.1) эквивалентно выражению:
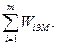 (3.2)
(3.2)
Анализ (3.2) показывает, что присоединяемые к элементарномк механизму структурные группы не влияют на подвижность простого или сложного механизма. Они только изменяют его структуру и законы движения звеньев.
Число подвижных контуров К, количество кинематических пар 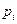 и количество звеньев n, входящих в структурную группу, можно установить с помощью структурных формул:
и количество звеньев n, входящих в структурную группу, можно установить с помощью структурных формул:
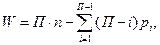 (3.3)
(3.3)
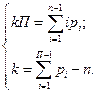 (3.4)
(3.4)
где 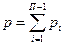 - общее число кинематических пар в механизме, П – подвижность пространства.
- общее число кинематических пар в механизме, П – подвижность пространства.
Для механизмов существующих в шестиподвижном пространстве (П=6), которые в технической литературе принято называть пространственные выражение (3.3) примет вид хорошо известной формулы Сомолова-Мальшева:
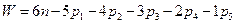
Для механизмов, существующих в трёхподвижном пространстве (плоских механизмов) П=3, выражение (3.3) примет вид формулы П.Л. Чебышева:
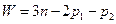
Так как по определению подвижность структурных групп равна нулю, то (3.3) для структурных групп примет следующий вид:
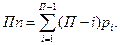 (3.3`)
(3.3`)
Формулы (3.3) и (3.4) описывают любую структурную группу Ассура.
Распишем, например, (3.3) для одно-, двух-, ... , шестиподвижных пространств. В результате получим следующие условия существования структурных групп в различных пространствах:
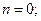 (3.5)
(3.5)
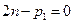 (3.6)
(3.6)
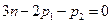 (3.7)
(3.7)
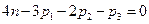 (3.8)
(3.8)
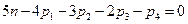 (3.9)
(3.9)
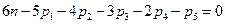 (3.10)
(3.10)
Из (3.5) следует, что в одноподвижном пространстве структурные группы существовать не могут, а это означает, что в одноподвижном пространстве механизмы не могут иметь замкнутых кинематических цепей, т.е. в таком пространстве могут существовать только механизмы с незамкнутыми кинематическими цепями.
Из (3.6) следует, что простейшей структурной группой (структурной единицей) является монада, которая состоит из одного звена и двух кинематических пар. На рис. 3.1 приведена в качестве примера структурная единица (монада), существующая в двухподвижном пространстве, которая используется для образования клинового механизма.
|
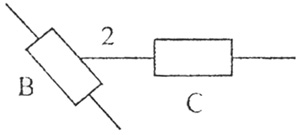 В соответствии с (3.6) эта монада имет одно звено 2 и две внешние кинематические пары С и В, которыми она затем присоединяется к стойке и звену 1 элементарного механизма. В результате этого образуется клиновой механизм.
В соответствии с (3.6) эта монада имет одно звено 2 и две внешние кинематические пары С и В, которыми она затем присоединяется к стойке и звену 1 элементарного механизма. В результате этого образуется клиновой механизм.
На рис.3.2, а представлена монада, существующая в трехподвижном пространстве, на основе которой созданы зубчатые и кулачковые механизмы. В соответствии с (3.7) эта монада должна иметь одно звено, одну одноподвижную и одну двухподвижную кинематические пары.
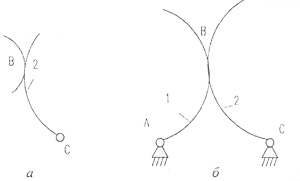
Рис. 3.2. Структурная единица и механизм, существующие и трехподвижном пространстве:
А - структурная единица; б - механизм; А,С - вращательная кинематическая пара; В - высшая двухподвижная кинематическая пара; 1 - звено элементарного механизма; 2 - структурная единица.
Присоединив эту монаду к элементарному механизму, получим простой механизм (рис. 3.2, 6), который является аналогом зубчатого и кулачкового механизмов.
Структурная группа, существующая в трехподвижном пространстве и имеющая только одноподвижные кинематичесие пары, в соответствии с (3.7) должна состоять из двух звеньев и трёх одноподвижных кинематических пар. Эта группа носит название диады Сильвестера или двухповодковой группы и приведена на рис. 3.3, а.
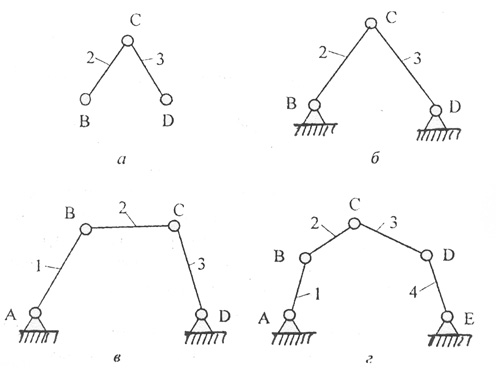
Рис. 3.3. Двухповодковая структурная группа и простые механизмы на её основе:
а - диада Сильвестера; б - статически определимая ферма, в - одноподвижный четырехзвенник;
г - двухподвижный пятизвенник; 1, 2 ... 4 ~ подвижные звенья; А, В ... Е - кинематические пары
Если двухповодковую группу связать шарнирами В и D со стойкой, то получим элементарную статически определимую ферму (рис.3.3, 6).
Присоединив эту двухповодковую структурную группу к одному неподвижному и одному или двум подвижным звеньям 1 и 4 элементарных механизмов, получим простой механизм с одной (рис.3.3, в) или двумя (рис.3.3, г) степенями свободы.
Дата добавления: 2017-02-13; просмотров: 1606;











