Неуправляемый выпрямитель при мгновенной коммутации

Рабочий процесс

Рабочие процессы рассмотрим в трехфазной нулевой схеме при следующих допущениях:

1. Неуправляемые вентили – идеальные: при протекании через них тока в проводящем направлении их сопротивление считается равным нулю и, значит, падение напряжения на них отсутствует. При приложении к ним обратного напряжения их сопротивление считается бесконечно большим, и, значит, обратный ток (i_обр) считается равным нулю.

2. Питающий трансформатор – идеальный: активное сопротивление обмоток трансформатора равно нулю и, главное, индуктивность рассеяния первичных и вторичных обмоток трансформатора равна нулю. Это значит, что токи в анодных цепях вентилей могут изменяться мгновенно, т.е. скачком.

3. Ток нагрузки идеально сглажен. Это может иметь место при бесконечно большой индуктивности в цепи нагрузки. При этом пульсирующая ЭДС преобразователя не будет вызывать пульсаций тока нагрузки.

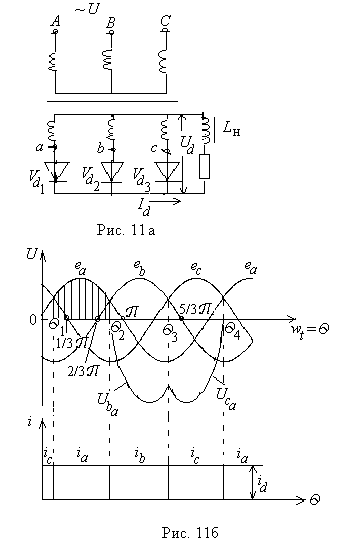
Фазные ЭДС вторичных обмоток трансформатора представлены тремя синусоидами, сдвинутыми каждая относительно предыдущей на угол 120° (электрических).

Направление фазных ЭДС определяют в зависимости от их полярности по отношению к проводящему направлению вентилей. Так на интервале 0 £ Q £ π ЭДС eа имеет прямую полярность по отношению к вентилю Vd1 , на интервале (2/3)p £ Q £ (5/3)p ЭДС eb - прямой полярности по отношению к вентилю Vd2 и т.д. На первом интервале фазная ЭДС eа, на втором ЭДС eb положительна. Рассмотрим состояние схемы на интервале Q₁£ Q£ Q₂. Здесь ЭДС eа имеет прямую полярность по отношению к V_d1. Учитывая, что на этом интервале eа > eb и eа > eс, к вентилям V_d2 и V_d3 приложены результирующие ЭДС обратной полярности и они заперты. Открыт и пропускает ток нагрузки только вентиль V_d1.

При Q= Q₂ eа = eb , а при Q> Q₂ eb > eа. Начиная с этого момента будет открыт вентиль V_d2 , ток нагрузки будет протекать по контуру фазы b, а к вентилям V_d1 и V_d3 будет приложено обратное напряжение, и они окажутся заперты.

Далее, ток нагрузки перейдет на фазу с и процессы в схеме будут повторяться. Таким образом, на интервале Q₁£ Q£ Q₂ ed = ea на интервале Q₂£ Q£ Q₃ ed = eb и на интервале Q₃£ Q£ Q₄ ed = ec . Мы видим, что ЭДС преобразователя изменяется по огибающей синусоид фазных ЭДС. Моменты, когда фазные ЭДС равны (моменты пересечения синусоид фазных ЭДС), носят название моментов (или точек) естественной коммутации. Сам же переход тока с вентиля предыдущей фазы на вентиль последующей фазы называется коммутацией. Таким образом, в неуправляемом выпрямителе с идеальным питающим трансформатором коммутация вентилей мгновенная и происходит в моменты естественной коммутации. Ток каждого из вентилей при указанных выше условиях и допущениях будет иметь форму прямоугольных импульсов угловой длительностью l_им= (2/3)p, чередующихся с паузами длительностью l_пауз= (4/3)p.

Величина ЭДС неуправляемого выпрямителя как было показано выше, мгновенные значения ЭДС неуправляемого выпрямителя изменяются по огибающей фазных ЭДС.

Для определения среднего значения ЭДС выпрямителя E_d0 необходимо проинтегрировать функцию ed(Q) на интервале повторяемости ((2/3)p) и отнести результат к величине интервала. Выберем в качестве такого интервала Q₁£ Q£ Q₂ , на котором

ed = ea = e_ф.max*sin Q (1)

где e_ф.max - амплитудное значение фазной ЭДС на вторичной стороне трансформатора.

Q- текущее значение электрического угла.

Тогда получим

((p/2)+( p/m_n ))

E_d0 = 1/(2p/m_n) ò e_ф.max ·sin Q dQ = (m/p)·sin(p/m)· e_ф.max =

((p/2)-( p/m_n ))

= Ö2· E₂·(m/p)·sin(p/m). (2)

здесь E₂ - действующее значение вторичной ЭДС питающего трансформатора.

Пределы интегрирования выбираются из следующих соображений: отсчет текущего значения угла Q осуществляется от точки пересечения синусоидой фазной ЭДС оси абсцисс при переходе этой ЭДС от отрицательной области в положительную, т.е. от точки 0. Отложив угол p/2, в нижнем, и в верхнем пределе интегрирования, мы оказываемся в точке амплитудного значения фазной ЭДС e_а. Нижний предел интегрированная – это точка естественной коммутации, совпадающая со значением угла Q₁. Для того, чтобы выйти в эту точку необходимо от точки амплитудного значения ЭДС eа вернуться назад на угол p/m_n. Это значение “угла возврата” получается путем деления на два интервала повторяемости, т.е. угловой длительности работы соответствующей фазы. Указанный интервал повторяемости составляет угол l= 2p/m _n.

Необходимо отметить, что полученная формула (2): Edo = √2· E2 · (m/π)· sin(π/m) справедлива не только для трехфазного нулевого выпрямителя, пульсность которого (m_n) равна трем, но и для любой другой пульсности. Величина пульсности связана с фазностью вентильных преобразователей формулой:

m _n= m · k_т

здесь: m – число фаз питающего трансформатора

k_т – число тактов выпрямительной схемы. Во всех нулевых схемах k_т = 1, в мостовых k_т = 2.

Верхний предел интегрирования получается путем прибавления к текущему значению угла, соответствующего точке амплитудного значения фазной ЭДС угла (p/m_n).

Величина и характер изменения обратного напряжения на вентилях. Обратимся к диаграмме напряжения (рис 11). Рассмотрим, как изменяется напряжение, прикладываемое к вентилю V_d1. На интервале Q₁£ Q£ Q₂ вентиль открыт, напряжение на нем равно нулю. С момента Q= Q₂ к вентилю V_d1 прикладывается обратное напряжение, изменяющееся, так как изменяется разность мгновенных значений ЭДС ea и eb . Эта разность есть не что иное, как линейное напряжение между фазами а и b.

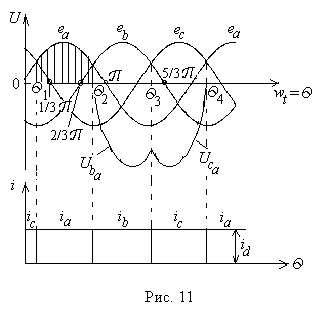
Указанное линейное напряжение прикладывается к вентилю V_d1 в непроводящем направлении, т.е. является для него обратным напряжением. Это напряжение действует в интервале Q₂ - Q₃.С момента Q₃ включается вентиль V_d3 , а вентиль V_d2 выключается. С этого момента к V_d1 прикладывается обратное напряжение U_ca. Как видно из диаграммы напряжений максимальное значение обратного напряжения на вентиле в трехфазной нулевой схеме равно амплитуде линейного напряжения на вторичной стороне питающего трансформатора.

U_обр.max = Ö3·Ö2·U_{2 ф} = 2,45·U_{2 ф} = 2,09·E_d0. (4)

Токи вторичных и первичных обмоток питающего трансформатора. Ток, протекающий по вторичным обмоткам трансформатора под действием ЭДС этих обмоток, обусловливает величину тока в нагрузке – I_d. Ток в нагрузке складывается из прямоугольных импульсов фазных токов и при принятых допущениях является идеально гладким. Вызывает интерес выяснить, какой ток, по форме и по величине, потребляется из питающей сети и протекает по первичным обмоткам питающего трансформатора. Это нужно знать для того, чтобы можно было ответить на вопрос, как влияет работа вентильного преобразователя на питающую сеть.

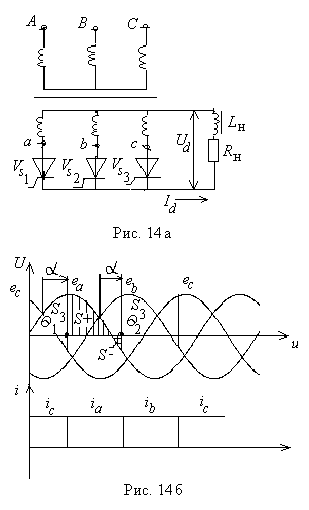
Рассмотрим эквивалентную схему неуправляемого вентильного преобразователя (выпрямителя), совмещенную с его питающим трансформатором.

Трансформатор включен по схеме звезда – звезда. Точками обозначено начало обмоток, а стрелками – положительное направление токов. Пренебрегая токами намагничивания трансформатора, ввиду их малости по сравнению с рабочими токами, и приняв для простоты k_тр =1 (w₁=w₂), напишем уравнения для магнитных контуров на основании 2-го закона Кирхгофа для магнитных цепей. Для этого обозначим два магнитных контура 1 и 2. Обходить контуры будем по направлению, указанному стрелкой. Условимся, что если ток совпадает по направлению с направлением обхода, он берется в уравнении со знаком “+”, если не совпадает – со знаком “-”. В соответствии со 2-м законом Кирхгофа, сумма токов в каждом замкнутом магнитном контуре должна быть равна нулю.

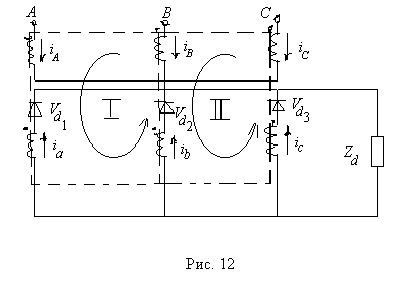
Кроме того, в соответствии с 1-ым законом Кирхгофа, сумма всех трех токов первичных обмоток трансформатора равняется нулю. На основании этих законов запишем систему уравнений:

i_A - i_a + i_b - i_B = 0

i_B - i_b + i_c - i_C = 0

i_A + i_B + i_C = 0 (5)

В этой системе шесть неизвестных: три значения первичных токов и три- вторичных. Однако вторичные токи могут быть определены из условий работы схемы. Так, для интервала Q₁£ Q£ Q₂ можно записать

i_a = i_d; i_b = i_c = 0

Тогда, решая систему, находим значения первичных токов

i_A= (2/3) I_d; i_B =i_C = -(1/3) I_d

Аналогично, для интервала Q₂£ Q£ Q₃ можно найти

i_B = (2/3) I_d ; i_A =i_C = -(1/3) I_d

Для интервала Q₃£ Q£ Q₄

i_C= (2/3) I_d; i_A =i_B = -(1/3) I_d

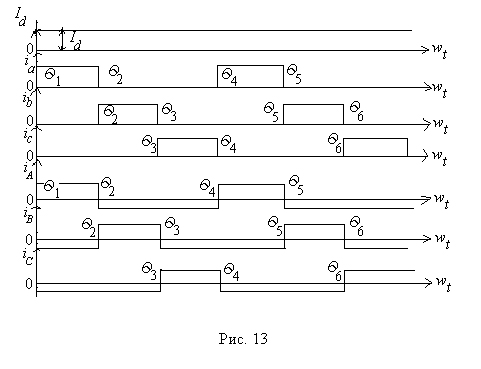
При принятых условиях и допущениях (k_тр =1, трансформатор и вентили идеальные) диаграммы токов во всех обмотках трансформатора выглядят следующим образом ( рис.13) ): при k_тр > 1 ((w₁/w₂)>1) первичные токи будут в k_тр раз меньше, чем те, которые определены по полученным формулам. Так для интервала Q₁£ Q£ Q₂

i_A= (1/ k_тр)·(2/3) I_d и т.д.

Суммарная намагничивающая сила по каждому из стержней в данной схеме оказывается отличной от нуля. Так, например, в стержне фазы А действует намагничивающая сила на интервале Q₁£ Q£ Q₂

F_A = (i_a - i_A)·w = (I_d – (2/3) I_d )·w = (1/3)w·I_d

на интервале Q₂£ Q£ Q₄

F_A = (i_a - i_A)· w = (0 – (1/3) I_d )·w = (1/3)w·I_d

Аналогичное наблюдается и в других стержнях трансформатора.

Таким образом, характерной особенностью трехфазной нулевой схемы является наличие некомпенсированных намагничивающих сил и вызванных ими потоков вынужденного намагничивания. Эти потоки замыкаются частично по сердечнику, по стальной арматуре трансформатора, частично по воздуху и при больших токах нагрузки могут привести к насыщению магнитопровода.

Для избежания этого приходится завышать сечение магнитопровода и, тем самым, утяжелять трансформатор, поэтому трехфазная нулевая схема в практике применяется нечасто и только для небольшой мощности электропривода. Поток вынужденного намагничивания возникает и при соединении первичных обмоток трансформатора по схеме “треугольника”.

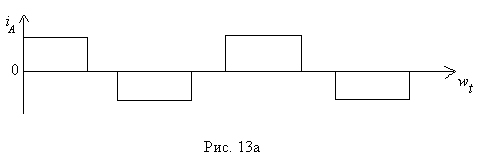
В других схемах преобразователей форма первичных токов отличается от рассмотренной выше. Так, в трехфазной мостовой схеме форма первичного тока симметрична относительно нулевого значения и имеет следующий вид ( рис.13,а)

Существует закономерность: чем ближе форма первичного тока питающего трансформатора к синусоиде, тем выше энергетические показатели схемы.

Существуют и используются схемы преобразователей с более высокими частотами пульсаций: двенадцатипульсные, двадцатичетырехпульсные и даже сорокавосьмипульсные. В них первичный ток по форме еще более приближается к синусоиде.

Тиристорный преобразователь при мгновенной

коммутации

Как было показано, неуправляемый выпрямитель может обеспечить только одно значение ЭДС на выходе (е_d0), т.е. максимально возможное в схеме. Для получения возможности регулирования величины ЭДС преобразователь выполняют управляемым, включая вместо неуправляемых вентилей тиристоры. Естественно, при этом необходимо организовать систему управления тиристорами. Однако, на начальном этапе рассмотрения работы управляемого преобразователя, будем предполагать, что включение тиристоров, т.е. подачу на их управляющие электроды импульсов, мы можем обеспечить в любой, желательный для нас, момент времени.

Если управляющие импульсы подавать на управляющие электроды тиристоров в моменты естественной коммутации, то получим так же, как и при неуправляемых вентилях, максимально возможную ЭДС E_d0. Регулирование ЭДС в сторону ее снижения осуществляется за счет задержки включения тиристоров относительно момента естественной коммутации. Величину этой задержки характеризует угол управления тиристорами преобразователя a.

Угол управления преобразователем a - это угол, выраженный в электрических градусах, отсчитываемый от точки естественной коммутации двух чередующихся фаз до момента включения тиристора последующей фазы.

Пусть управляющий импульс на тиристор V_s1 подан в момент Q = Q₁. Обратим внимание на то, что к этому моменту ток в фазе С протекает встречено с фазной ЭДС за счет энергии, накопленной в индуктивности нагрузки рабочим током.

Подача управляющего импульса тиристор V_s1 включает, а тиристор V_s3 - выключает. Далее при Q = Q₂ с тем же углом задержки a подается управляющий импульс на V_s2 и ток с фазы а коммутируется на фазу b и т.д.

На рис 14(а) показана форма ЭДС преобразователя, а на рис.14(б) токи, протекающие по фазным обмоткам трансформатора в предположении идеальной сглаженности тока I_d и мгновенной коммутации фазных токов с предыдущей на последующую фазу.

Анализ диаграммы напряжения показывает следующее:

- при увеличении угла a, E_d преобразователя снижается. Величина этого снижения, определяемая вольт – секундной площадкой Sз, тем больше, чем больше угол a.

- ЭДС преобразователя при a > 30° содержит участки как положительных (S+), так и отрицательных (S-) значений вольт – секундных площадок. С увеличением угла a (S+) уменьшаются, а (S-) увеличиваются.

- импульсы фазных токов трансформатора, сохраняя прямоугольную форму, смещаются в сторону отставания на величину угла a по отношению к точке естественной коммутации.

Величина ЭДС тиристорного преобразователя. Принцип, определения среднего значения ЭДС на выходе тиристорного преобразователя, тот же, что и для определения среднего значения ЭДС неуправляемого преобразователя: определяется площадь, заключенная между кривой, отражающей функцию изменения фазной ЭДС, и осью абсцисс. Эта вольт - секундная площадь, с учетом ее знака, определяется в пределах интервала повторяемости как определенный интеграл, нижний и верхний пределы которого соответствуют границам интервала повторяемости. Зная отношение вычисленной площади к длине интервала повторяемости, вычислим среднее значение ЭДС тиристорного преобразователя для интересующей нас величины угла a.

E_d0 =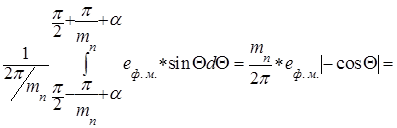

=(m_n /2p) e_ф.м.{cos{(p (m_n -2)/2m_n )+a }- cos {(p (m_n +2)/2m_n )+a }}

= e_ф.м (m_n /p) sin (p /m_n) cos a = E_d0 cos a.

Таким образом, выявлена очень простая зависимость, связывающая величину средней выпрямленной ЭДС на выходе тиристорного преобразователя E_d и величину максимально возможной ЭДС этого ТП с углом управления a:

E_d = E_d0 * cos a.

Ее графическое представление называют регулировочной характеристикой ТП (рис.15а)

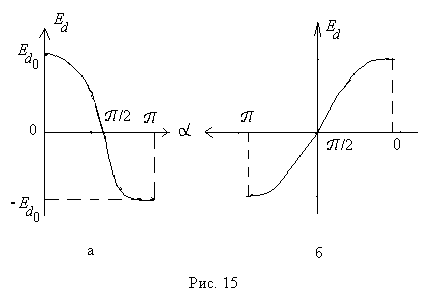
Иногда угол a на оси абсцисс откладывается иначе (рис.15б). На оси абсцисс может откладываться другая переменная, связанная с углом a линейной, или нелинейной зависимостью. Этот вопрос будет рассмотрен при изложении систем управления ТП.

Коммутация токов в фазах питающего трансформатора ТП при переключении вентилей

Ранее процесс перехода тока с одной фазы трансформатора на другую рассматривался как мгновенный. Это было обусловлено принятыми допущениями. В реальных схемах из – за наличия в цепях переменного тока индуктивных сопротивлений, в частности индуктивных сопротивлений обмоток трансформатора, процесс коммутации имеет определенную длительность. Индуктивные сопротивления обмоток трансформатора, обусловленные потоками рассеяния в магнитной системе, определяются из опыта короткого замыкания трансформатора, и в расчетах учитываются в виде общей индуктивности L_S, представляющей собой суммарную индуктивность рассеяния вторичной обмотки и приведенную к ней индуктивность первичной обмотки. Влияние на процесс коммутации активных сопротивлений обмоток трансформатора учитывать не будем из – за его незначительности.

По – прежнему выпрямленный ток считаем идеально сглаженным (wL_н = ¥). На рис.16 представлена эквивалентная схема трехфазного нулевого выпрямителя (а) и диаграммы напряжений и токов (б), поясняющие процесс коммутации токов.

Индуктивные сопротивления обмоток учтены введением в схему индуктивностей L_S . Предположим, что в проводящем состоянии находится вентиль V_S1 . В момент Q₁ поступает включающий импульс на вентиль V_S2 . Поскольку потенциал анода вентиля в этот момент положителен относительно катода, вентиль включается.

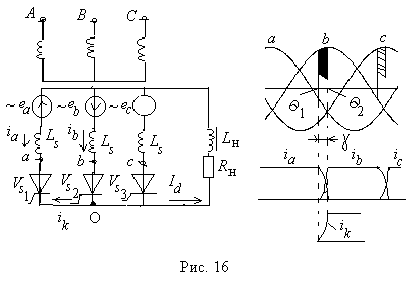
Начиная с момента Q₁ оба тиристора включены и две фазы (а и b) вторичной обмотки трансформатора оказываются замкнутыми через них накоротко. Под воздействием ЭДС обмоток этих фаз (e_à и e_b) в короткозамкнутой цепи (контура коммутации) появляется ток короткого замыкания i_k, который является коммутирующим током.

Этот ток можно в любой момент интервала коммутации (Q₂ - Q₁ ) определить по формуле

i_k = (U_2m/2Xs)*{cos a - cos (a + Q)} (6)

где U_2m – амплитудное значение линейного напряжения между фазами a и b;

Xs= wL_S ; (7)

a - угол управления.

Нужно отметить, что через вентиль V_S1 фазы а ток i_k протекает в непроводящем направлении. Такое возможно, т.к. вентиль V_S1 смещен прямым током I_d , протекавшем через него до начала коммутации. Ток i_k направлен от фазы b с большим потенциалом к фазе а с меньшим потенциалом. Учитывая, что выпрямленный ток I_d при wL_н =¥ в интервале коммутации остается неизменным, можно, согласно первому закону Кирхгофа для точки 0 записать

i_a + i_b + I_d = 0 ;

или с учетом направления токов

i_a + i_b = I_d = const.

Последнее уравнение справедливо для любого момента интервала коммутации. Пока ток проводит только вентиль V_S1 , получаем i_a = I_d и i_b = 0. На интервале одновременной проводимости вентилей V_S1 и V_S2 (интервал коммутации тока с фазы а на фазу b): i_a = I_d - i_k и i_b = i_k.

Когда коммутация закончится и ток будет проводить только вентиль V_S2, получим

i_b = I_d ; i_a = 0.

Из рис.16 видно, что в интервале от Q₁ до Q₂ ток i_b плавно увеличивается, а i_a уменьшается. Когда ток i_b станет равным I_d , а ток i_a снизится до нуля, вентиль V_S1 выключится и ток нагрузки будет продолжать протекать только через вентиль V_S2

Длительность интервала коммутации характеризуется углом коммутации g, который может быть определен из следующего уравнения (для трехфазной нулевой и трехфазной мостовой схем):

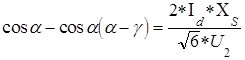
Обозначив угол коммутации g при угле управления a = 0 через g₀, можно записать

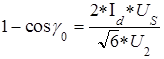
Подставляя в исходное уравнение значение g₀, получаем

g = arccos {cos a + cos g₀ - 1} - a .

Согласно последней формуле с ростом угла a (в пределах 0<a<90°) уменьшается угол коммутации g . Физическая сущность этого явления состоит в том, что с увеличением угла a (в указанных пределах) растет напряжение, под действием которого возрастает ток i_k в контуре коммутации и, следовательно, до значения I_d он нарастает быстрее. При дальнейшем росте угла a (90°<a<180°) угол коммутации увеличивается.

Процесс коммутации оказывает непосредственное влияние на выпрямленное напряжение U_d . Это связано с тем, что при изменении фазных токов в зоне коммутации в индуктивностях L_s обмоток трансформатора появляются ЭДС самоиндукции. В выходящей из работы фазе ЭДС самоиндукции складывается с ЭДС e_a. Во вступающей в работу фазе ЭДС самоиндукции вычитается из e_b. Таким образом, с учетом действия ЭДС самоиндукции мгновенное значение выпрямленного напряжения на интервале коммутации тока равно полусумме ЭДС коммутируемых фаз:

U_d = (U_a + U_b)/2 ,

где U_a и U_b - мгновенные значения фазных напряжений вторичной обмотки трансформатора.

Так как в зоне коммутации мгновенное значение выпрямленного напряжения снижается, по сравнению с мгновенной коммутацией, до величины U_d , происходит уменьшение среднего значения выпрямленного напряжения. Его величина определяется выражением

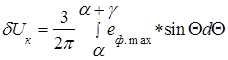(8)

Из (6), (7), и (8) можно получить

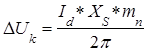(9)

Анализируя последнюю формулу, мы видим, что от двух первых множителей, стоящих в числителе, зависит ширина заштрихованной на диаграмме площадки. От значения множителя m_n зависит количество этих площадок, приходящихся на период переменного напряжения 2p.

В завершение рассмотрения процесса коммутации фазных токов обратим внимание на то, что коммутационное снижение средней величины выпрямленного напряжения не зависит от действующего значения переменного напряжения на вторичных обмотках питающего трансформатора, а также от величины угла управления a. Оно зависит только от трех величин, входящих в формулу (9).

Внешние характеристики тиристорных преобразователей.

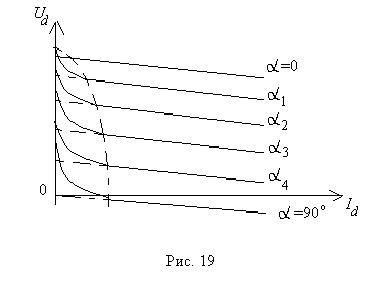
Внешней характеристикой ТП называется зависимость выпрямленного напряжения от среднего значения тока нагрузки при неизменной величине угла управления a (рис.17):

U_d = ¦(I_d)

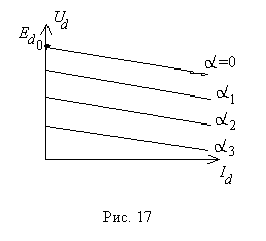
Внешняя характеристика определяется внутренним сопротивлением преобразователя, которое приводит к снижению выпрямленного напряжения с ростом нагрузки.

Снижение напряжения обусловлено тремя факторами:

- коммутационным падением напряжения (dU_k).

- падением напряжения в активных сопротивлениях цепей преобразователя, по которым протекают токи (dU_R).

- падением напряжения в вентилях (dU_B).

Соответственно внешнюю характеристику ТП (при wL_н = ¥) можно записать в виде

U_d = E_d0cos a - dU_k - dU_R - dU_В. (10)

В зависимости от мощности выпрямителя влияние активных и реактивных элементов схемы в этом процессе различно. Обычно в маломощных выпрямителях преобладает влияние активного сопротивления обмоток трансформатора, а в мощных – индуктивного сопротивления.

Следует отметить, что при значениях тока нагрузки, не превышающих номинальные, внутреннее падение напряжения ТП (при a = 0), как правило, составляет не более 10 – 15% напряжения E_d0.Однако при перегрузках и режимах, близких к короткому замыканию, существенно влияние внутренних сопротивлений схемы.

Представляет также интерес вид внешних характеристик при малых токах нагрузки. Это связано с тем, что имеется много электроприводов, обслуживающих механизмы с пульсирующим либо знакопеременным моментом или требующих частого изменения направления скорости вращения, т.е. реверса механизма. В этих случаях ток снижается до нуля или, даже, изменяет свое направление. Для выполнения таких функций используются реверсивные ТП, состоящие из двух преобразователей, позволяющих изменять направление тока. При этом, ТП часто работает с малыми токами, имеющими, иногда, нулевое значение. В таком случае, внешние характеристики ТП меняют свой вид, т.к. в действие вступают совсем другие соотношения, которые описывают другие физические процессы.

При значительном снижении тока допущение его идеальной слаженности, что имеет место при wL_н = ¥, принято быть не может. Реальная индуктивность нагрузки не только не в состоянии идеально сгладить выпрямленный ток, но она даже не может обеспечить его непрерывность. Ток становится прерывистым и, в этом режиме работы, внешние характеристики теряют свою линейность, затрудняя управление преобразователями.

С уменьшением тока резко возрастает напряжение ТП из-за явлений, связанных с прерывистым характером тока якоря, когда вентиль предыдущей фазы прекращает проводить ток до момента включения вентиля последующей фазы. При этом, угловая длительность прохождения тока в вентиле l становится меньше, 2p/m_n.

Эти явления особенно сильно сказываются при больших углах управления a ТП. Уравнение (10) справедливо лишь тогда, когда ток в нагрузке протекает непрерывно. Если принято, что индуктивность L_н в цепи выпрямленного тока бесконечно большая, то непрерывность будет иметь место при любых значениях тока. Если же L_н имеет конечную величину, то непрерывное протекание тока возможно лишь при превышении некоторого граничного значения I_{dгр .}

Величина последнего согласно [1] может быть подсчитана по приближенному уравнению

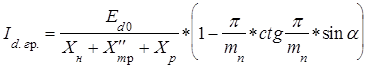
здесь X"mр, Xн и X_р - приведенные ко вторичной обмотке индуктивные сопротивления трансформатора, нагрузки и сглаживающего реактора.

В трехфазной нулевой схеме E_d0 определяется через фазные напряжения трансформатора, в трехфазной мостовой – через линейные. При этом m_n = 6.

Для мгновенных значений напряжения якорной цепи при отсутствии перекрытия вентилей (g = 0) справедливо уравнение

e₂ - E_я = i*R_я.ц. + L (di/dt) + dU_в (11)

где R_я.ц. = R_я + R_тр + R_р ; L = L_я + L_тр + L_р

dU_в - падения напряжения в вентилях;

e₂ и i - мгновенные значения вторичной ЭДС трансформатора и тока.

E_я - ЭДС якоря двигателя.

В выражении (11) ЭДС трансформатора изменяется по синусоидальному закону. ЭДС двигателя в установившемся режиме из – за инерционности вращающихся масс не может заметно измениться за время интервала пульсаций и считается постоянной. При этом разность ЭДС, в левой части уравнения, в какие- то моменты положительна, а в какие – то отрицательна. Однако при больших токах в индуктивностях якорной цепи запасается такое количество электромагнитной энергии, которого достаточно для поддержания тока прежнего направления в промежутках времени, когда e₂ - E_я < 0 и, даже, на протяжении части отрицательной полуволны напряжения трансформатора, когда e₂ < 0. Ток в анодной цепи вентиля поддерживается за счет ЭДС самоиндукции ( 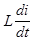) при убывании тока. Поэтому при достаточно больших значениях индуктивности и тока последний не прерывается и выпрямленная ЭДС преобразователя определяется средним значением ЭДС трансформатора за интервал повторяемости выпрямленной ЭДС (T_п = 2p/m_n).

При малых нагрузках (рис.18) ток под действием противо – ЭДС двигателя снижается до нуля (момент Q₂) раньше момента включения последующего вентиля. В результате ток через якорь при малых нагрузках на валу двигателя проходит не непрерывно, а отдельными импульсами.

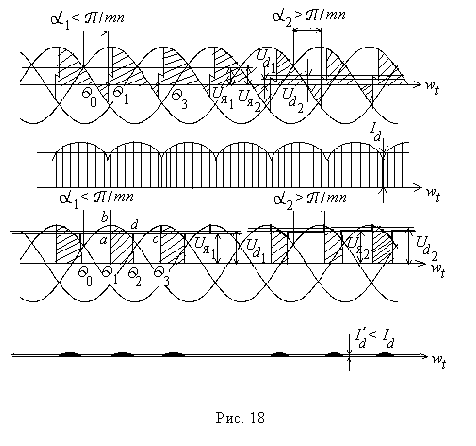
Выражение (11) справедливо только для интервалов времени, в течение которых ток проходит по цепи якоря. В промежутках между импульсами тока вращение якоря поддерживается за счет механической энергии вращающихся масс, а напряжение на выходных клеммах преобразователя равно ЭДС якоря двигателя E_я .Этим объясняется тот факт, что в режиме прерывистого тока среднее значение выпрямленного напряжения, измеряемое на нагрузке и определяемое площадью между кривой abcde и осью абсцисс, деленной на интервал повторяемости, по мере снижения нагрузки резко возрастает. Чем меньше ток, тем раньше наступит его прерывание и тем выше окажется среднее выпрямленное напряжение. В результате этого крутизна внешних характеристик ТП при малых нагрузках резко возрастает.

В соответствии с рис.19 в режиме прерывистого тока среднее значение выпрямленного напряжения на зажимах двигателя определится выражением

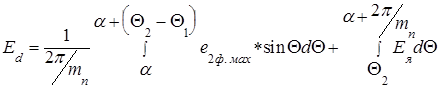(12)

где e_2ф.max - амплитудное значение фазной ЭДС вторичной обмотки трансформатора;

Q₁ и Q₂ - соответственно углы включения и выключения вентилей, отсчитываемые от начала синусоиды линейной ЭДС трансформатора.

Выражение E_d = E_d0 cos a получается из (12), как частный случай, если положить l = 2p/m_n , где l - интервал проводимости вентиля.

В режиме непрерывных токов, когда l = 2p/m_n имеет место однозначное соответствие между E_d и Ða . В режиме прерывистого тока среднее выпрямленное напряжение на двигателе зависит не только от величины ЭДС трансформатора e₂ и угла управления преобразователя a, но и от величины тока, т.е. от величины момента нагрузки на валу двигателя и индуктивности цепи якоря двигателя. Аналитическое выражение для внешних характеристик в области прерывистого тока в явном виде получить нельзя, т.к. напряжение и ток связаны трансцендентными уравнениями.

Тем не менее, существуют методы расчета внешних характеристик и в области прерывистого тока. Их следует использовать при выполнении курсового проекта.

Инверторный режим работы тиристорных преобразователей.

Инвертированием называется процесс преобразования электрической энергии постоянного тока в энергию переменного тока. Термин “инвертирование” происходит от латинского inversio – переворачивание, перестановка. Впервые этот термин в преобразовательных устройствах был применен для обозначения процесса, обратного выпрямлению, при котором поток энергии изменяет свое направление на обратное и поступает от источника постоянного тока в сеть переменного тока. Такой режим был назван, в противоположность выпрямительному режиму, инверторным, а преобразователь, осуществляющий процесс передачи энергии от источника постоянного тока в сеть переменного тока, - инвертором. Поскольку электрические параметры преобразователя на стороне переменного тока (частота переменного тока, действующее значение напряжения) в этом случае полностью определяются параметрами сети, то такой инвертор называют зависимым, или ведомым сетью.

Исторически термин “инвертор” распространился на все виды статических преобразователей электрической энергии постоянного тока в переменный.

Источник и приемник энергии постоянного тока.

Для рассмотрения и выяснения признаков источника и приемника электрической энергии рассмотрим работу электромашинной системы, используемой на подъемных установках, например шахтных подъемниках. Иногда в шахтах возникает необходимость выполнить, операцию перегона порожних подъемных сосудов.

В исходном состоянии правый подъемный сосуд (рис.20) находится в верхнем положении, левый – в нижнем. Цель перегона – поменять подъемные сосуды местами: правый переместить вниз, левый поднять вверх.

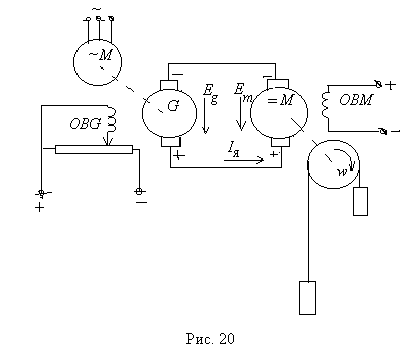
Вес пустых подъемных сосудов одинаков и они уравновешивают друг друга, если не учитывать веса подъемного каната, но не учитывать нельзя, т.к. на глубоких его вес достигает нескольких тонн. В начале перегона электрическая машина =М должна развивать двигательный момент для движения вверх левого сосуда вместе с тяжелым подъемным канатом. Когда подъемные сосуды окажутся в середине шахтного ствола, напротив друг друга, левая и правая ветви уравновесятся, а при дальнейшем движении правая, более длинная ветвь каната, спускаясь, будет раскручивать шкив Ш, а значит, и якорь машины =М, под действием спускаемого подъемного сосуда и более длинной ветви каната. Машина =М должна оказывать тормозное воздействие на раскручиваемый грузом шкив.

Рассмотрим виды преобразования энергии и направление этой энергии при выполнении операции перегона. В начале этой операции электрическая машина ~М, потребляя из сети переменного тока электрическую энергию, т.е. работая в режиме электрического двигателя, преобразует ее в механическую энергию вращающегося вала, который вращает якорь электрической машины постоянного тока G. Эта машина, будучи возбужденной, и работая в режиме генератора постоянного тока, преобразует полученную механическую энергию в электрическую энергию постоянного тока. Эта энергия, в виде тока и напряжения по проводам поступает на якорь машины =М, где преобразуется в механическую энергию вращающегося шкива Ш и энергию, необходимую для подъема левого подъемного сосуда вместе с канатом.

Таким образом электрическая энергия потребляется из сети переменного тока, претерпевает ряд преобразований, и, в конечном счете, используется для выполнения механической работы. Назовем такое направление энергии прямым.

Теперь рассмотрим режимы работы электрических машин постоянного тока G и =М. Машина G работает в режиме генератора постоянного тока. Она создает ЭДС E_G, под действием которой создается ток в якорной цепи обеих машин.

В статическом режиме работы ток I_я определяется выражением:

I_я = (E_G - E_М )/ å R_я.ц (19)

Такое выражение для тока I_я связано с тем, что ЭДС E_М направлена встречно с ЭДС E_G и величина тока зависит от разности этих ЭДС. Так как в начале процесса перегона груз оказывает тормозящее действие на якорь машины =М, ее ЭДС, зависящая от частоты вращения, меньше, чем ЭДС E_G и направление тока в якорной цепи совпадает с направлением ЭДС E_G.Эта сонаправленность ЭДС и тока является единственным признаком источника электрической энергии постоянного тока.

Встречное направление ЭДС и тока характерно для приемника электрической энергии.

Эти признаки источника и приемника электрической энергии очень важны для понимания физических процессов, происходящих во многих электротехнических устройствах.

По мере перемещения левой ветви каната с подвешенным к ней подъемным сосудом вверх происходит снижение нагрузки на вал двигателя =М, частота вращения его увеличивается и возрастает ЭДС E_М