Опровержение: определение и виды.
1. Определение и структура доказательства.Доказательство – это особая логическая процедура. Оно производно от суждения. В доказательстве ход рассуждений идет от обосновываемого суждения к другим истинным суждениям, которые рассматриваются в качестве его посылок. В доказательстве и доказываемое суждение, и обосновывающее его суждение известны. Здесь требуется установить логическую связь между этими суждениями. Доказательство – это логическое действие, направленное на обоснование истинности суждения с помощью других истинных суждений на основании их логической связи.
Структура доказательства:
Тезис доказательства (от греч. Jέοη – положение, утверждение) – это суждение, истинность которого необходимо обосновать.
Аргументы доказательства (от лат. argumentum – довод, основание доказательства) – это используемые для обоснования тезиса суждения, истинность которых либо очевидна, либо обоснована ранее.
Форма доказательства, или демонстрация(от лат. demonsratio – показывание) – это логическая связь между аргументами и между аргументами и тезисом доказательства.
Пример доказательства, т.е. обоснования тезиса в данном случае сформулированного Полем С. Брэггом в начале высказывания: «Купить здоровье нельзя, его можно только заработать своими собственными постоянными усилиями: только упорная и настойчивая работа над собой позволит каждому сделать себя энергичным долгожителем, наслаждающимся бесконечным здоровьем. Я сам заработал здоровье своей жизнью. Я здоров 365 дней в году, у меня не бывает никаких болей, усталости, дряхлости тела. И вы можете добиться таких же результатов!»
Логическая связь между тезисом и аргументами устанавливается по правилам дедуктивного, индуктивного или традуктивного умозаключения. Поэтому доказательство является логической операцией с суждениями, в ходе которой используются умозаключения.
Если обозначить аргументы и тезис доказательства пропозициональными переменными – символами суждений, а логическую связь – символом необходимого логического следования, то формула доказательства будет представлять собой сложное комбинированное суждение, сочетающее нематериальную импликацию и конъюнкцию:
(p 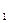
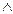 р
р 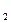
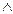 p
p 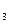 …
… 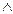 p
p 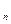 )→t
)→t
Среди видов тезисов иногда выделяют:
– основной тезис, т.е. положение, с которого вытекают (или ему подчиняются) несколько явно сформулированных положений, в связи с чем доказательство основного тезиса предполагает обоснование этих подчиненных положений;
– подчиненный тезис или частичный тезис, т.е. положение, которое становится тезисом потому, что благодаря ему доказывается основной тезис, а это обусловливает то, что доказанный частичный тезис становится аргументом для основного тезиса.
Главное, что тезис должен быть истинным, ибо неистинное положение, которое выдвигается как тезис, невозможно обосновать никаким доказательством.
Виды аргументов в доказательстве:
– удостоверенные единичные факты – это так называемый фактический материал, т.е. статистические сведения (о населении, территории государства, количестве вооружения, свидетельские показания, подпись лица на документе, научные данные, научные факты);
– определения как аргументы доказательства – это определения понятий формулируемые в каждой науке (математике, химии, физике, биологии, географии и др.);
– аксиомы и постулаты, т.е. исходные положения (суждения) наук, принимающиеся в качестве аргументов без доказательства;
– дефиниции, т.е. определения, которые, раскрывая содержания понятия, являются концентрированным знанием о предмете, в связи с чем ссылка на дефиницию является достаточной для определения истинности тезиса;
– ранее доказанные законы науки и теоремы как аргументы доказательства – это прежде доказанные законы природы (физики, химии, биологии и др.), законы общества (экономики, права, морали и др.), которые могут служить аргументами в процессе доказательства.
Данные виды аргументов в ходе доказательства могут использоваться не по одному, а в сочетании друг с другом.
Виды демонстрации в доказательстве:
– дедуктивная демонстрациязаключается в отнесении частного случая к общему правилу, в роли которого выступают достоверно установленные факты, отражающиеся в частных или общих суждениях, либо законы науки, также различной степени обобщения;
– индуктивная демонстрация предполагает обоснование тезиса, отражающего группу единичных явлений (класс или часть класса), с помощью нескольких аргументов, отражающих единичные случаи, принадлежащие этому классу;
– традуктивная демонстрация характеризуется одинаковой степенью обобщения, присущей тезису и аргументам, например, когда и в тезисе, и в аргументах отражаются признаки единичных явлений, либо когда и в тезисе, и в аргументах отражаются признаки множества (подмножества) элементов.
2. Виды и правила доказательства.В зависимости от отношения между составляющими доказательство суждениями – тезисом и аргументами – выделяют два вида доказательств: прямое и косвенное.
Прямое доказательство – это доказательство, в котором не используются противоречащие тезису аргументы. Иначе говоря, доказательство идет от рассмотрения аргументов к обоснованию тезиса, т.е. истинность тезиса непосредственно обосновывается аргументами.
Схема прямого доказательства: из данных аргументов (a, b, c…) необходимо следует доказываемый тезис (q).
Прямое доказательство широко используется в статистических отчетах, различного рода документах, в постановлениях, в художественной литературе, науке (напр.:«Все углеводы горючи. Сахар – углевод. Следовательно, сахар – горюч»).
Следует заметить, что, поскольку тезис и аргументы с точки зрения логической формы представляют собой суждения, постольку в прямом доказательстве и тезис, и аргументы должны иметь одинаковое качество: если тезис является утвердительным суждением, то утвердительными суждениями должны быть и аргументы. И наоборот, если тезис является отрицательным суждением, то и аргументы должны быть отрицательными суждениями. Тождество качества суждений, выражающих тезис и аргументы, можно рассматривать как специальное правило данного вида доказательства, дополняющее общие правила тезиса и аргументов. С точки зрения объединенной качественно-количественной классификации, суждение-тезис и суждения-аргументы не могут находиться в отношениях противоположности, подпротивоположности и противоречия.
Например, требуется обосновать тезис: «Теория постиндустриального общества Д. Белла не основана на технологическом детерминизме». Суть доказательства сводится к дедуктивному умозаключению, подводящему тезис под общие законы и принципы научной методологии. Они таковы: «Теория, не основанная на непосредственной детерминации организации общества формой организации техники, индустриальной системы производительных сил, не является теорией технологического детерминизма»; «Теория постиндустриального общества Д. Белла является теорией, которая не основана на непосредственной детерминации организации индустриального общества формой организации машинных производительных сил». По правилам модуса ЕАЕ первой фигуры простого категорического силлогизма из этих посылок необходимо следует вывод, представляющий собой исходный тезис: «Теория постиндустриального общества Д. Белла не является теорией технологического детерминизма». В этом силлогизме содержащая больший термин большая посылка и тезис, выступающий заключением, являются отрицательными суждениями. Между ними устанавливается отношение подчинения, причем, большая посылка – общеотрицательное суждение – является подчиняющим, а тезис – единичноотрицательное суждение – подчиненным. Между тезисом и аргументом-меньшей посылкой отношение несравнимости, которое также исключает противоречие, поскольку противоречащими могут быть только сравнимые суждения.
Выделяют два вида прямого доказательства: обусловливающее и соединительное.
– обусловливающее доказательство – это прямое доказательство, в котором используется дедуктивная демонстрация.
Пример с теорией Д. Белла является обусловливающим доказательством, т.к. ход доказательства представляет собой восстановление дедуктивного умозаключения – простого категорического силлогизма первой фигуры, и в доказательстве не использовались противоречащие тезису суждения.
– соединительное доказательство – это прямое доказательство, в котором используется индуктивная демонстрация.
Например, требуется обосновать тезис «Система торговли У. Галлахера является рентабельной». Для этого исследуют факты, наблюдаемые при применении этой системы на биржевом рынке валютных пар, сырьевых или товарных контрактов за определенный период. В одних случаях применяют размерность, предложенную самим У. Галлахером (10 дней), в других – иные размерности, тестируя систему в процессе купли-продажи различных инструментов в течение длительного периода времени. В итоге устанавливают, что в 80-90% случаев эта система торговли обеспечивает прибыль от незначительной до высокой. Таким образом, по схеме неполной научной индукции делается вероятностный вывод о том, что тезис истинен.
Косвенное (непрямое) доказательство – это доказательство, в котором используется противоречащее тезису суждение – антитезис (от греч. αντιJέοη – противоположение), т.е. в непрямом доказательстве истинность выдвинутого тезиса обосновывается путем неистинности антитезиса.
Антитезис образуется посредством отрицания тезиса. Если тезис обозначить буквой a, то его отрицание будет антитезисом – ~а, т.е. противоречащим тезису суждением. В сложном суждении строгой дизъюнкции для каждого из дизъюнктов, взятого в роли тезиса, другие дизъюнкты будут выступать в качестве антитезисов.
Выделяют два вида косвенного доказательства: апагогическое и разделительное:
– апагогическое доказательство (или доказательство «от противного»)– это косвенное доказательство посредством установления неистинности антитезиса.
Пусть а – тезис (или теорема), который необходимо доказать. Предполагаем от противного, что а неистинно, т.е. истинно не-а (или ~а). Из допущения ~а выводим следствия, которые противоречат действительности или ранее известным теоремам. Имеем а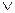 ~а, при этом ~а неистинно, значит истинно его отрицание, т.е. ~ ~а, которое по закону двузначной классической логики (~ ~а→а) дает а. Значит, истинно а, что и требовалось доказать.
~а, при этом ~а неистинно, значит истинно его отрицание, т.е. ~ ~а, которое по закону двузначной классической логики (~ ~а→а) дает а. Значит, истинно а, что и требовалось доказать.
Иначе говоря, в апагогическом доказательстве сначала выдвигается антитезис и делается допущение о его истинности. Затем антитезис рассматривается как антецедент импликации, в результате которой из антитезиса выводятся несколько суждений-следствий. Суждения-следствия сопоставляются с фактами (суждениями, истинность которых уже установлена), и в результате устанавливается несовместимость следствий с этими истинными суждениями, а значит, неистинность следствий. По закону импликации, если следствие неистинно, то импликация может быть истинной только при неистинности основания (в данном случае тезиса). Таким образом, в силу закона исключенного третьего допущение об истинности антитезиса, как и сам антитезис, признается неистинным, а тезис, наоборот, – истинным. Доказательство завершается.
Апагогическое доказательство может применяться тогда и только тогда, когда суждение-тезис и суждение-антитезис находятся в отношении противоречия (контрадикторности);
– разделительное доказательство – это косвенное доказательство, при котором тезис является членом закрытой дизъюнкции, посредством установления неистинности всех других ее членов.
Разделительное доказательство применяется, когда тезису противопоставляют не одно, а несколько полностью или частично несовместимых с ним суждений. При этом рассуждение соответствует формуле отрицающе-утверждающего модуса разделительно-категорического силлогизма:
<p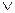 q
q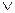 r>
r>
pÙr
q,где q – тезис, а суждения p и r – антитезисы.
При этом демонстрация является дедуктивной, и в процессе доказательства необходимо учитывать специальное правило отрицающе-утверждающего модуса: в большей посылке должны быть перечислены все альтернативы. В противном случае дедуктивное умозаключение об истинности тезиса не будет следовать с необходимостью, и доказательство окажется несостоятельным.
Например: Преступление могли совершить только либо p, либо q, либо r. Доказано, что не совершали преступления ни p (p), ни r (r). Следовательно, преступление совершил q.
Тем самым истинность тезиса устанавливается путем последовательного доказательства неистинности всех членов разделительного суждения, кроме одного.
Следует добавить, что в отрицающе-утверждающем модусе разделительно-категорического силлогизма союз «или» может употребляться не только как нестрогая дизъюнкция (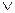 ), но и как строгая дизъюнкция (
), но и как строгая дизъюнкция ( 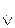 ):
):
<p 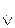 q
q 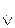 r>
r>
pÙr
q
Для всех элементов доказательства (тезиса, аргументов и демонстрации) существуют определенные правила.
Правила доказательства:
– Правила тезиса доказательства:
1. тезис должен быть точным, ясным и непротиворечивым;
2. на всем протяжении доказательства тезис должен быть неизменным, тождественным себе.
Поскольку тезис по форме является суждением, первое правило предполагает полную логическую характеристику суждения и его терминов: точное выявление словосочетаний, их выражающих, установление количества и качества суждения, отношения между терминами, видов выражающих их понятий. Если термин является новым, требуется выполнить операцию определения выражающего его понятия.
– Правила аргументов доказательства:
1. аргументы доказательства тезиса должны быть истинными суждениями;
2. аргументы должны быть суждениями, истинность которых доказана самостоятельно, независимо от тезиса, т.е. истинность аргументов не должна зависеть от тезиса;
3. аргументы должны быть достаточным основанием для доказательства тезиса, т.е. тезис должен следовать из аргументов с необходимостью.
Первое правило аргументов указывает на существование логической связи между операцией доказательства суждения и умозаключением. Фактически доказательство есть операция восстановления полного умозаключения по одному его элементу – заключению. Истинность доказательства, таким образом, предполагает истинность умозаключения, отражающего связь между тезисом и аргументами. Важнейшим критерием логической правильности умозаключения является истинность посылок, которые в доказательстве выступают в качестве аргументов. Если это требование нарушается, то умозаключение, устанавливающее связь между аргументами и тезисом, оказывается логически неправильным, а указанная связь – неустановленной. В результате доказательство не выполняется, т.к. его основной существенный признак – обоснование тезиса – отсутствует.
Второе правило аргументов логически следует из первого. Кроме того, оно основано на определении и на направленности мысли в процессе доказательства. Главная цель и одновременно существенный признак доказательства – обоснование тезиса. В соответствии с первым правилом аргументы при этом должны быть истинными. Это значит, что если их истинность неочевидна (напр., аргументы не отражают аксиом или законов науки), то ее следует установить (доказать). Но в любом доказательстве можно обосновывать только тезис, а не аргументы. Таким образом, сначала потребуется доказать каждый из аргументов, что возможно только в рамках отдельного доказательства, в котором будущий аргумент выступит в качестве тезиса. Но если истинность аргументов зависит от истинности тезиса, то тезис становится аргументом по отношению к аргументам, а каждый из аргументов становится тезисом по отношению к тезису. Поэтому совместить в одном доказательстве обоснование и тезиса, и аргументов невозможно. Это ведет к разрушению логической структуры доказательства.
Очевидно, что и в правилах тезисов, и в правилах аргументов отражаются также общие законы логики: второе правило тезиса представляет закон тождества в применении к тезису, а третье правило аргументов представляет закон достаточного основания в применении к аргументам.
– Правила демонстрации доказательства – это правила умозаключения, поскольку демонстрация представляет собой умозаключение, а потому ее правила таковы: общие правила терминов и посылок или специальные правила фигур силлогизма, правила индукции или традукции (умозаключений по аналогии).
3. Ошибки в процессе доказательства. При нарушении правил доказательства возникают ошибки.
Ошибки в процессе рассуждения могут быть преднамеренными и непреднамеренными.
Ошибки рассуждений, возникающие в результате непреднамеренного нарушения правил логики, называются паралогизмами (от греч. παράλογισμος – неправильное рассуждение).
Ошибки, возникающие при преднамеренном нарушении правил логики с целью ввести в заблуждение оппонентов, называются софизмами (от греч. σοφισμα – хитрость, выдумка, уловка).
Наиболее распространенные ошибки доказательства:
Ошибки тезиса, которые возникают вследствие нарушения первого и второго правил, заключаются в полной или частичной подмене тезиса.
– Полная подмена тезиса выражается в использовании в переходе в процессе доказательства от тезиса к близкому, но не тождественному ему суждению.
Существует две основные формы полной подмены тезиса: довод к человеку и довод к публике («логическая диверсия»):
– довод к человекузаключается в изложении в процессе доказательства не аргументации, логически связанной с тезисом, а использование в качестве аргументов суждений, выражающих личные качества доказывающего или слушателей. Это попытка переключить внимание на объективные или субъективные обстоятельства их жизни, профессиональной деятельности, создать благоприятное впечатление о себе, вызвать какие-либо чувства, к примеру, симпатии или жалости, показать не относящуюся к тезису эрудицию и т.п.
Например, довод к человеку характерен для обоснования новизны диссертации, содержания статей или монографий, где вместо самой новизны, доказательства ценности работы приводятся цитаты из высказываний крупных ученых, видных деятелей, полагая, что одних ссылок на авторитет достаточно. Этот же довод характерен для преподавательской деятельности при выставлении оценки, когда она обоснована не результатом знаний студента, а, скажем, оправдывается ссылками на его личные качества.
– довод к публике состоит в том, что внимание с доказываемого тезиса переключается на события, актуальные для аудитории, но логически с тезисом не связанные.
Например, довод к публике имел место в военной агрессии США против Ирака. Вместо доказательства наличия (реально отсутствовавших) средств массового поражения, элементов технологии производства ядерного оружия, американская администрация утверждала о диктатуре иракских властей и нарушении прав человека, т.е. апеллировала к нарушению традиционно значимых для американского общества демократических ценностей.
Существует широкая группа подобного рода ошибок: довод к силе, выгоде, невежеству, здравому смыслу, верности, авторитету, состраданию и т.п.
– Частичная подмена тезиса выражается в попытке расширить тезис, сделать его более строгим, или напротив, смягчить, нивелировать.
Имеются две основные формы частичной подмены тезиса: слишком широкое доказательство и слишком узкое доказательство, ошибки которых заключаются в изменении количества выражающего тезис суждения.
Пример: Ошибка слишком широкого доказательства произойдет, если тезис – частноутвердительное суждение «В некоторых сферах украинской экономики наблюдается рост» – заменить общеутвердительным суждением «В украинской экономике наблюдается рост». А такая подмена достаточно часто имеет место в выступлениях как среди представителей исполнительной власти, так и в среде оппозиционеров, которым легче опровергнуть тезис о росте экономики в целом, чем имеющийся налицо рост экономики в отдельных сферах. Ошибка слишком узкого доказательства состоит, соответственно, в замене общего тезиса частным или единичным, либо частного тезиса – единичным. Так, нередко в случае выявления на суде ошибок при проведении следственных действий обвинение переходит от тезиса о том, что обвиняемый виновен в совершении всех инкриминируемых ему преступлений к тезису о виновности только в совершении некоторых из них.
Ошибки аргументов.
Наиболее распространенные ошибки аргументов: «основное заблуждение» (от лат. error fundamentalis), «предвосхищение основания» (petitio principii), логический круг (circulus in devonstrando), «от сказанного в относительном к сказанному в абсолютном смысле»:
– Основное заблуждение (или ложность основания) – это использование неистинного аргумента в качестве истинного.
Такая ошибка может быть непреднамеренной.
Примером является геоцентрическая система Птолемея, построенная на основании неистинного допущения о вращении Солнца вокруг Земли. Подобная ошибка часто возникает при неполной индуктивной демонстрации, когда все существенные факты эмпирически установить невозможно при расследовании преступления в случае отсутствия достаточного количества свидетельских показаний, содержащих только косвенные улики против обвиняемого.
Эта же ошибка может быть и преднамеренной (софизмом), совершенной с целью запутать, ввести в заблуждение (напр., при даче ложных показаний свидетелями или обвиняемыми в ходе судебного расследования, неправильное опознание вещей или людей и т.п.).
– Предвосхищение основания – это использование в качестве аргументов суждений, истинность которых проблематична.
Ошибка выражается в опоре на расхожие мнения, достоверно не установленные факты, слухи и т.п., которые принимаются на веру, считаются истинными без доказательства. В итоге, недоказанные аргументы не доказывают тезис, а только предвосхищают его.
Так, подобного рода ошибку представляют собой выделенные Ф. Бэконом так называемые «идолы театра», заключающиеся в слепой вере в авторитеты – в бездоказательном, некритическом восприятии постулатов известных философов прошлого, даже в случаях, когда они заблуждались.
– Логический круг – это использование аргументов, истинность которых зависит от истинности тезиса. Здесь тезис обосновывается аргументами, а аргументы обосновываются этим же тезисом (напр.: «Винтовая лестница – та, которая построена в форме винта»).
Такая ошибка – прямое следствие нарушения второго правила аргументов.
Например, подобную ошибку совершал Дж. Беркли, который доказывал несуществование материи – всеобщего объективного бытия, основываясь на абсолютности и всеобщности бытия субъективного. Любое бытие, по Дж. Беркли, – это существование чего-либо в сознании субъекта в форме чувственно воспринимаемых им идей. Материальные вещи также воспринимаются посредством чувственных идей (ощущений), значит они, как считал философ, являются субъективными. Но аргумент в субъективности бытия не был им обоснован, т.к. истинность этого аргумента он определял исходя из тезиса о невозможности бытия объективного. В результате Дж. Беркли вопрошал: «Для чего трудиться рассуждать о материи, разве изобретение чего-либо находящегося за пределами сознания не есть нечто немыслимое?»
– «От сказанного в относительном к сказанному в абсолютном смысле» характеризуется теми же признаками, что и ошибка слишком широкого доказательства, только в применении не к тезису, а к аргументам.
Такая ошибка специфична для популярной индукции, делающей на основании констатации единичных признаков общий вывод о классе явлений.
Так, эта ошибка отражается в установленных Ф. Бэконом «идолах рода», когда из-за присущей всем людям склонности к поспешным обобщениям отдельные, наиболее удобные факты принимаются за всеобщие, и возникают так называемые «антиципации природы». Например, Анаксимен полагал, что мироздание, представляющее собой плоский диск, заканчивается за горами, окружающими море, омывающее Грецию, поскольку именно там находится линия горизонта, ограничивающая диапазон зрительного восприятия мира. Другие же эмпирические факты, свидетельствующие о независимости строения макрокосма от чувственного восприятия субъекта, равно как и гелиоцентрическая модель мироздания, тогда не были известны, что и послужило основой подобного рода обыденно-индуктивного вывода.
Дата добавления: 2017-02-13; просмотров: 2579;











