Параллельно соединенные индуктивность, емкость и активное сопротивление в цепи синусоидального тока

К схеме на рис. 6.12 подключено синусоидальное напряжение 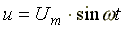. Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.

Определим ток на входе схемы.

В соответствии с первым законом Кирхгофа:

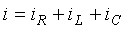, (6.19)

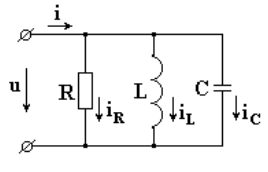где

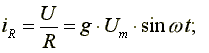
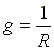- активная проводимость.

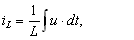
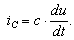
Рис. 6.12 Подставим эти формулы в уравнение (6.19). Получим:

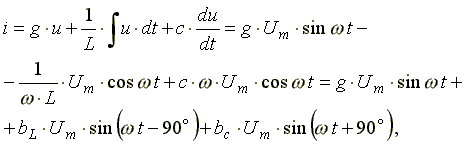, (6.20)

где 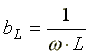- индуктивная проводимость;

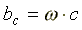- емкостная проводимость.

Из уравнения (6.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.

Запишем уравнение (6.20) в комплексной форме.

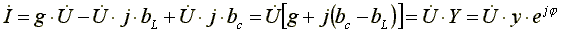, (6.21)

где 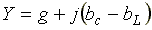- комплексная проводимость;

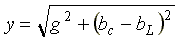- полная проводимость;

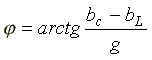- начальная фаза комплексной проводимости.

Построим векторные диаграммы, соответствующие комплексному уравнению (6.21).

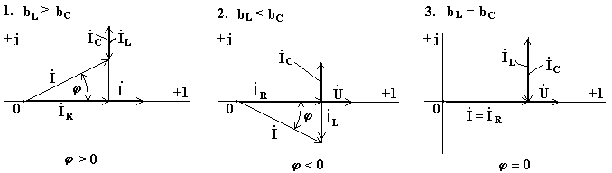
Рис. 6.13 Рис. 6.14 Рис. 6.15

В схеме на рис. 6.12 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.

Из условия возникновения резонанса тока 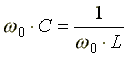получим формулу для резонансной частоты тока

.

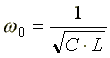В режиме резонанса тока полная проводимость цепи 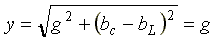- минимальна, а полное сопротивление 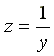- максимально. Ток в неразветвленной части схемы 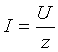в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,

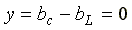и .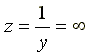

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой.