Прохождение микрочастицы сквозь потенциальный барьер. Туннельный эффект
Возможность прохождения микрочастицы сквозь потенциальный барьер, т.е. проникновение микрочастицы через область пространства, в которой её полная энергия 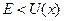 является чисто квантовым эффектом (туннельнымэффектом), в основе которого лежит волновая природа свойств вещества.
является чисто квантовым эффектом (туннельнымэффектом), в основе которого лежит волновая природа свойств вещества.
Покажем основные этапы этого явления для частицы с энергией 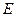 преодолевающей потенциальный барьер высотой
преодолевающей потенциальный барьер высотой 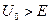
U(x)= 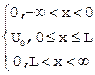
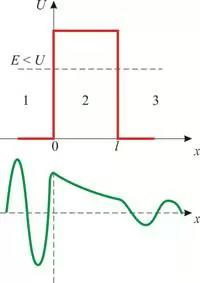
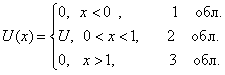
В соответствии с законами классической механики 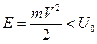 частица в области 1 движется вдоль оси X равномерно и прямолинейно, а затем, отразившись от барьера в точке X=0, движется в обратном направлении с
частица в области 1 движется вдоль оси X равномерно и прямолинейно, а затем, отразившись от барьера в точке X=0, движется в обратном направлении с 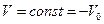 (в разрешённой области).
(в разрешённой области).
Поведение квантовой частицы будет подчиняться уравнению Шрёдингера, которое будет выглядеть по-разному в 1-ой и 3-ей где 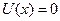 , и во 2-ой области где
, и во 2-ой области где 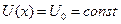 . Используя свойства непрерывности, зададимся, чтобы на границе, т.е. при х=0, были равны функции ψ1=ψ2 и их производные
. Используя свойства непрерывности, зададимся, чтобы на границе, т.е. при х=0, были равны функции ψ1=ψ2 и их производные
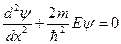 (1-я и 3-я область)
(1-я и 3-я область)
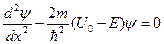 (2-я область)
(2-я область)
Общее решение в 1-й области, где 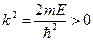 , имеет вид суперпозиции падающей
, имеет вид суперпозиции падающей 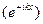 и отражённой
и отражённой 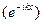 плоских волн де Бройля:
плоских волн де Бройля:
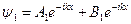 1-я область
1-я область
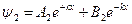 2-я область кроме характеристического ур-я (14) действительны
2-я область кроме характеристического ур-я (14) действительны
и равны 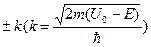
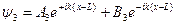 3-я область
3-я область
Const интегрирования 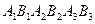 находятся из условия непрерывности волновой функции и её первой производной на графике
находятся из условия непрерывности волновой функции и её первой производной на графике 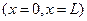 и условия нормировки. На рис.2б изображено схематично решение уравнения
и условия нормировки. На рис.2б изображено схематично решение уравнения 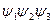 . Амплитуда
. Амплитуда 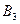 прошедшей волны
прошедшей волны 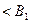 амплитуды падающей волны, что указывает на частичное преодоление и частичное отражение микрочастицы от барьера. Вероятность прохождения микрочастицы без изменения энергиисквозь барьер определяется коэффициентом прозрачности Д, который для прямоугольного барьера высотой
амплитуды падающей волны, что указывает на частичное преодоление и частичное отражение микрочастицы от барьера. Вероятность прохождения микрочастицы без изменения энергиисквозь барьер определяется коэффициентом прозрачности Д, который для прямоугольного барьера высотой 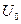 и шириной
и шириной 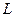 :
:
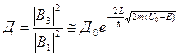

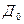 - коэффициент пропорциональности, по своей величине близкий к 1.
- коэффициент пропорциональности, по своей величине близкий к 1.
Наличие в показателе 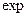 чрезвычайно малой величины
чрезвычайно малой величины 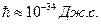 приводит к тому, что Д большая для классических частиц, масса которых достаточно велика, поэтому их движение определяется законами Ньютона.
приводит к тому, что Д большая для классических частиц, масса которых достаточно велика, поэтому их движение определяется законами Ньютона.
Оценим Д: пусть 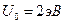 при
при 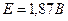
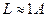
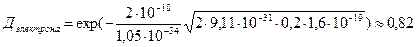
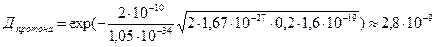
Т.о преодоление 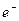 такого барьера представляет собой практически достоверное событие (Д=0,82), а протон
такого барьера представляет собой практически достоверное событие (Д=0,82), а протон 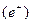 с той же энергией уже не может преодолеть этот барьер.
с той же энергией уже не может преодолеть этот барьер.
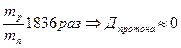
Значит Д, помимо m, сильно зависит от ширины барьера L, увеличение L в 3 раза приводит к уменьшению Д в 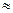 20 раз(
20 раз( 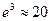 ).
).
Если 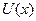 представляет собой потенциальный барьер, то коэффициент преломления n волн де Бройля по его границе при
представляет собой потенциальный барьер, то коэффициент преломления n волн де Бройля по его границе при 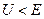
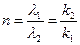
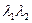 - длины волн де Бройля в 1-й 2-й областях
- длины волн де Бройля в 1-й 2-й областях
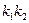 - соответствующие значения волновых чисел
- соответствующие значения волновых чисел
Рассмотренный туннельный эффект объясняет такие явления, как ионизация атомов и вырывание электронов из металлов под действием эл. поля, 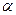 -распад атомных ядер и многие другие явления, происходящие в полупроводниковых приборах.
-распад атомных ядер и многие другие явления, происходящие в полупроводниковых приборах.
Коэффициент отражения 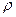 при прохождении волн де Бройля через низкий
при прохождении волн де Бройля через низкий 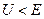 потенциальный барьер
потенциальный барьер  ширины:
ширины:
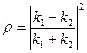
| <== предыдущая лекция | | | следующая лекция ==> |
| Электрон в атоме водорода | | | Структура и виды кристаллических решёток, их характеристики. |
Дата добавления: 2017-01-26; просмотров: 1637;











