Структура и виды кристаллических решёток, их характеристики.
Твердыми называются тела, обладающие постоянством формы и объема. Устойчивость твердого состояния обеспечивается природой химических связей между частицами вещества, когда энергия связи становится значительно больше кинетической энергии теплового движения самих частиц. Под кристаллом понимают твёрдые вещества с упорядоченной внутренней структурой.
Различают кристаллические твердые тела и аморфные. При низких температурах термодинамически устойчивым состоянием всех веществ является кристаллическое. Однако в зависимости от свойств частиц кристаллизация может потребовать значительного времени, чтобы частицы успели перестроиться при охлаждении. Если молекулы вещества сильно переплетены, то уже в жидком состоянии это вещество обладает высокой вязкостью, препятствующей перегруппировке частиц при его охлаждении. В результате кристаллическое состояние практически не реализуется. Вещество при этом находится в твердом состоянии и представляет собой переохлажденную жидкость. Такое состояние вещества, характерное для высокомолекулярных соединений, называется аморфным.
Кристаллическое тело характеризуется правильным расположением атомов в пространстве. У аморфных веществ расположение атомов случайно. Кристаллические вещества образуют кристаллическую решётку.
Кристаллическая решётка характеризуется элементарной ячейкой.
Однако под словом "кристалл" можно понимать любую систему (не обязательно систему атомов), в которой отдельные элементы выстраиваются в правильную решетку. Это могут быть, например, вихри, заключенные в ограниченный объем, расталкивающиеся коллоидные частицы на поверхности жидкости и многие другие системы. Главное, чтобы отдельные физические объекты "чувствовали" друг друга, чтобы система вела себя как целое, а не разваливалась на части.
Элементарная ячейка – кристаллическая решётка наименьшего объёма, воспроизведение которой в пространстве множество раз создаёт пространственную кристаллическую решётку. Атомы в пространстве располагаются упорядоченно, образуя кристаллическую решётку.
Основу симметрии бесконечной кристаллической решётки составляет её пространственная периодичность — способность совмещаться с собой при параллельных переносах (трансляциях) на определённые расстояния в определённых направлениях. Эквивалентные узлы кристаллической решётки, которые могут быть совмещены друг с другом путём трансляции, образуют Браве решётку. Их существует 14 типов.
По симметрии Браве решётки делятся на 7 кристаллических сингоний. Кроме того, кристаллическая решётка может обладать осями и плоскостями симметрии, зеркально-поворотными и винтовыми осями и плоскостями зеркального скольжения. Совокупность осей и плоскостей симметрии, определяющая симметрию физических свойств кристаллов, называется кристаллическим классом; их 32.

Совокупность всех элементов симметрии кристаллической решётки называется её пространственной группой. Всего возможно 230 различных пространственных групп
Для описания элементарной ячейки кристаллической решетки используют 6 величин:
- Три отрезка, равные расстояниям a,b,c(периоды решетки) до ближайших частиц по осям координат, и три угла 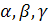 между этими отрезками. Соотношения между этими величинами определяются симметрией, согласно которой все кристаллы подразделяют на 7 систем.
между этими отрезками. Соотношения между этими величинами определяются симметрией, согласно которой все кристаллы подразделяют на 7 систем.
- Координационное число – число ближайших равноудаленных частиц (для ОЦК – К8, для простой кубической решетки – К6, для ГЦК – К12).
- Коэффициент компактности – отношение объема всех частиц, приходящихся на 1 элементарную ячейку, ко всему объему элементарной ячейки (для простой кубической решетки 0,52, для ОЦК – 0,68, для ГЦК – 0,74).
Кристаллографические индексы (Индексы Миллера): Они выбираются следующим образом
– находятся точки, в которых данная плоскость пересекает оси координат. Координаты записываются в единицах постоянных решетки;
– берутся обратные значения полученных чисел, приводятся к общему (наименьшему) знаменателю и знаменатель отбрасывается. Плоскости обозначаются индексами в круглых скобках – (h k 1). Если плоскость пересекает ось в области отрицательных значений координат, то соответствующий индекс пишется с верхней чертой.
Например, пусть плоскость пересекает оси координат в точках с координатами х=3, у=-2, z=1. Обратные значения – 1/3; -1/2; 1. Приведя к общему знаменателю и отбросив его, можно записать индексы Миллера данной плоскости как ( 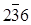 ). Если плоскость параллельна какой-либо координатной оси, то соответствующий индекс будет равен нулю. Поэтому плоскостям, пересекающим грани куба по диагонали, соответствуют обозначения (110), (101), (011), а плоскости граней куба обозначаются (100), (010), (001). Чем больше величина какого-либо индекса Миллера плоскости, тем ближе к началу координат расположено место ее пересечения с соответствующей осью. На рис.1. показаны примеры обозначения некоторых плоскостей в кубическом кристалле.
). Если плоскость параллельна какой-либо координатной оси, то соответствующий индекс будет равен нулю. Поэтому плоскостям, пересекающим грани куба по диагонали, соответствуют обозначения (110), (101), (011), а плоскости граней куба обозначаются (100), (010), (001). Чем больше величина какого-либо индекса Миллера плоскости, тем ближе к началу координат расположено место ее пересечения с соответствующей осью. На рис.1. показаны примеры обозначения некоторых плоскостей в кубическом кристалле.
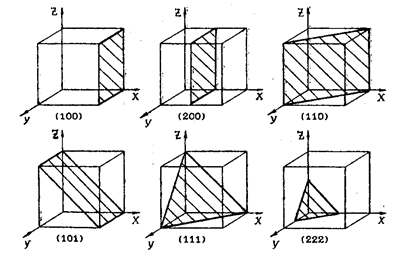
Рис.1. Главные плоскости в кубическом кристалле и их индексы Миллера
- Индексы направления – выражаются целыми числами 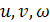 в единицах отрезков
в единицах отрезков 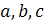 , заключаются в квадратные скобки
, заключаются в квадратные скобки 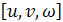 .
.
- Индексы плоскости – определяют положение плоскости в пространстве. Выражаются целыми числами 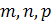 в единицах отрезков
в единицах отрезков 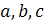 . За индексы берутся обратные отрезки:
. За индексы берутся обратные отрезки: 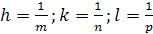 .
.
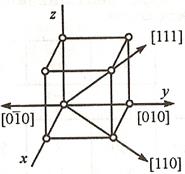
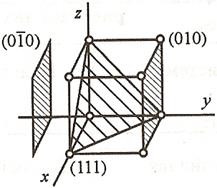
Рис.2.1
Дата добавления: 2017-01-26; просмотров: 3357;











