Электрон в атоме водорода
Постулаты Бора
Постулаты Бора определили направление развития новой науки – квантовой физики атома. Но они не содержали рецепта определения параметров стационарных состояний (орбит) и соответствующих им значений энергии En.
Правило квантования, приводящее к согласующимся с опытом значениям энергий стационарных состояний атома водорода, Бором было угадано. Он предположил, что момент импульса электрона, вращающегося вокруг ядра, может принимать только дискретные значения, кратные постоянной Планка. Для круговых орбит правило квантования Бора записывается в виде
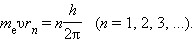
Здесь me – масса электрона, υ – его скорость, rn – радиус стационарной круговой орбиты. Правило квантования Бора позволяет вычислить радиусы стационарных орбит электрона в атоме водорода и определить значения энергий. Скорость электрона, вращающегося по круговой орбите некоторого радиуса r в кулоновском поле ядра, как следует из второго закона Ньютона, определяется соотношением
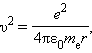
где e – элементарный заряд, ε0 – электрическая постоянная. Скорость электрона υ и радиус стационарной орбиты rn связаны правилом квантования Бора. Отсюда следует, что радиусы стационарных круговых орбит определяются выражением
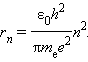
Самой близкой к ядру орбите соответствует значение n = 1. Радиус первой орбиты, который называется боровским радиусом, равен
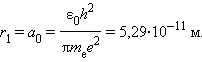
Радиусы последующих орбит возрастают пропорционально n2.
Полная механическая энергия E системы из атомного ядра и электрона, обращающегося по стационарной круговой орбите радиусом rn, равна
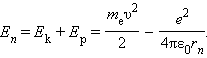
Следует отметить, что Ep < 0, так как между электроном и ядром действуют силы притяжения. Подставляя в эту формулу выражения для υ2 и rn, получим:
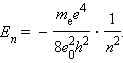
Целое число n = 1, 2, 3, ... называется в квантовой физике атома главным квантовым числом.
Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с энергией En на другую стационарную орбиту с энергией Em < En атом испускает квант света, частота νnm которого равна ΔEnm / h:
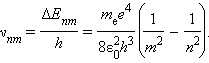
Эта формула в точности совпадает с эмпирической формулой Ридберга для спектральных серий атома водорода, если положить постоянную R равной
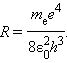
Подстановка числовых значений me, e, ε0 и h в эту формулу дает результат
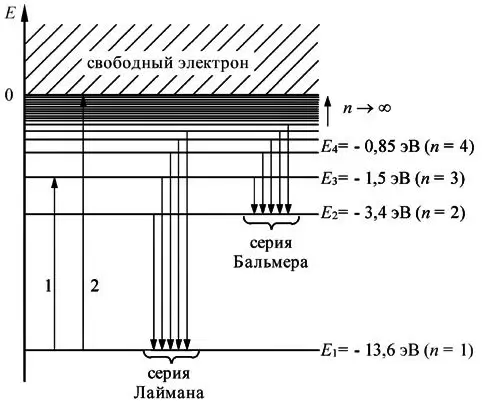
R = 3,29·1015 Гц, который очень хорошо согласуется с эмпирическим значением R. Рис. 1 иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.
Электрон в атоме водорода
Потенциальная энергия взаимодействия электрона с ядром в атоме водорода равна
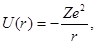
| (1.14) |
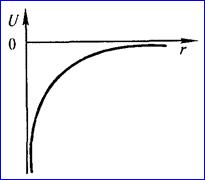
где r — расстояние между электроном и ядром, которое в первом приближении будем считать точечным. Графически функция U(r) изображена жирной кривой на рис. 1.5 а. U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает. Уравнение Шрёдингера в этом случае имеет вид
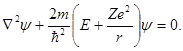
| (1.15) |
Решение уравнения (1.15) проводят методом разделения переменных с учетом естественных требований, налагаемых на ψ-функцию: она должна быть однозначной, конечной, непрерывной и гладкой. В теории дифференциальных уравнений доказывается, что решения уравнения являются непрерывными, однозначными и конечными в следующих случаях:
1) при любых положительных непрерывных значениях энергии;
2) при дискретных отрицательных значениях энергии.
Первый случай соответствует свободному электрону (заштрихованная область на рис. 1.5 б), второй — получаемым из уравнения Шрёдингера собственным значениям энергии
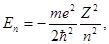 n = 1, 2, 3, … n = 1, 2, 3, …
| (1.16) |
Случай (Е < 0) соответствует связанным состояниямэлектрона в атоме.
Решение уравнения Шрёдингера приводит в случае Е < 0 к формуле (1.16) для энергетических уровней без использования каких-либо дополнительных постулатов (в отличие от первоначальной теории Бора). Кроме того, совпадение с формулой Бора означает, что мы пришли к той же самой системе энергетических уровней, как в теории Бора. Это же относится и к частотам излучения при переходах между уровнями.
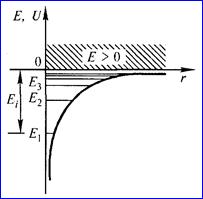
Таким образом, решение уравнения Шрёдингера приводит для атома водорода к появлению дискретных энергетических уровней Е1, Е2, ..., Еп, показанных на рис. 1.5 б в виде горизонтальных прямых.
а) б)
Рис. 1.5 . а - потенциальная энергия U(r) и б - собственные значения энергии Е электрона в атоме водорода.
Самый нижний уровень Е1, отвечающий минимальной возможной энергии, — основной, все остальные (Еп > Е1 , п = 2, 3, ...) — возбужденные. При Е < 0 движение электрона является связанным — он находится внутри гиперболической потенциальной ямы. Из рисунка следует, что по мере роста главного квантового числа п энергетические уровни располагаются теснее и при п → ∞ Е∞ → 0.
При Е > 0 движение электрона является свободным; область непрерывного спектра Е > 0 (заштрихована на рис. 1.5 б) соответствует ионизированному атому.
Различие в интерпретации с теорией Бора относится только к состояниям электрона: в теории Бора это движение по стационарным орбитам, здесь же орбиты теряют физический смысл, их место занимают ψ-функции.
Диаграмма энергетических уровней (рис.1.5) позволяет дать несколько важных определений.
Энергия возбуждения Евоз– это энергия, которую необходимо сообщить электрону, чтобы он из основного состояния (n = 1) перешёл в возбужденное. Например, Евоз = 10,2 эВ – энергия, необходимая для перехода электрона в состояние, соответствующее n = 2 (первое возбужденное состояние).
Энергия ионизации Еион– энергия, необходимая для отрыва электрона, находящегося в основном состоянии (n = 1), от ядра, т.е. для перевода электрона на уровень с n= ∞ . Для атома водорода энергия ионизации равна 13,6 эВ.
Из анализа следует три вывода.
· Электрон в атоме может иметь только дискретные значения энергии. В любом атоме энергии электронов дискретны.
· Существует состояние электрона с энергией, меньше которой электрон иметь не может. Это состояние называется основным. Все остальные состояния называют возбужденными. При этом, двигаясь с ускорением, любая заряженная частица излучает электромагнитные волны. На этом принципе устроены все антенны, любые источники электромагнитного излучения - радиоволн, видимого света, рентгеновских и гамма-лучей. А электрон в атоме, в каком бы состоянии он ни находился, не излучает, хотя движется с ускорением. Электрон в возбужденном состоянии может излучить электромагнитную энергию, перейдя в одно из состояний с меньшей энергией. Энергия излучается квантами, и в процессе излучения, как во всех процессах, происходящих в природе, выполняется закон сохранения энергии. Энергия излученного кванта в соответствии с законом сохранения энергии равна hn = = En - Em, где n и m - целые числа и n > m. Сколько времени электрон проведет в возбужденном состоянии, зависит от целого ряда причин, исследованных квантовой механикой. Эти времена различны, но все они конечны.
· Как исключение, основное состояние электрона в атоме устойчиво, поскольку закон сохранения энергии запрещает электрону, находящемуся в основном состоянии, излучать электромагнитную энергию.
| <== предыдущая лекция | | | следующая лекция ==> |
| Использование файлов, проецируемых на память | | | Прохождение микрочастицы сквозь потенциальный барьер. Туннельный эффект |
Дата добавления: 2017-01-26; просмотров: 5502;











