В ЛАЗЕРНОЙ ДИАГНОСТИКЕ

ПРИМЕНЕНИЕ МЕТОДОВ СПЕКЛ-ИНТЕРФЕРОМЕТРИИ

Понятие спекла тесно связано с понятием когерентного объема, введенным в предыдущей главе. Напомним: когерентным объемом называется объем области конфигурационного пространства, соответствующей элементу фазового пространства, т.е. про распространении со скоростью c волны, испускаемой источником с поперечным сечением s и занимающей полосу частот Dn, это объем с протяженностью ~ с/Dn вдоль направления распространения волны и поперечным размером в пределах дифракционного угла (т.е. в пределах угла, внутри которого угловые размеры источника не превышают диска Эйри).

В принципе, имея концепцию когерентного объема, можно было бы обойтись без специальных терминов, рассматривая отражение когерентного излучения от диффузно отражающих поверхностей. Однако, исторически сложившееся понятие «спекл» как характерное расстояние между областями с максимальной и минимальной интенсивностями при отражении когерентного излучения от диффузной поверхности стало привычным (напомним, что по-английски «speckle» означает пятнышко, метку). В общем случае свойства спекл-картины зависят от степени когерентности источника и структуры рассеивающей поверхности.

Различают (по терминологии родоначальника голографии и спекл-интерферометрии Д. Габора) объективную и субъективную спекл-картины. Объективной (см. рис. 25.1) называется спекл-картина, наблюдаемая на некотором расстоянии L от диффузно рассеивающей поверхности при диаметре D падающего на поверхность пучка излучения. Если падающее излучение с длиной волны l полностью когерентно, а характерный размер неоднородностей на поверхности мал по сравнению с D, то поперечный размер спекла для объективной картины равен:

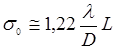(25.1)

что с очевидностью следует из самой концепции когерентного объема.

Рис. 25.1.

Образование объективной спекл-структуры.

D – диаметр засвеченной области на объекте, L – расстояние между объектом и плоскостью образования картины.

Объективной спекл-картина называется так потому, что любая, даже сколь угодно малая ее часть получает излучение от всей рассеивающей поверхности. Если же между наблюдателем и диффузно отражающей поверхностью поставить линзу (оптическую систему), то картина спеклов, сформированная в плоскости изображения, будет называться субъективной. В этом случае малая область спекл-картины завязана только на определенную часть облученной поверхности (см. рис. 25.2).

Субъективная спекл-структура дает возможность извлекать нужную информацию из рассеянного излучения, управляя параметрами фокусирующей оптической системы.

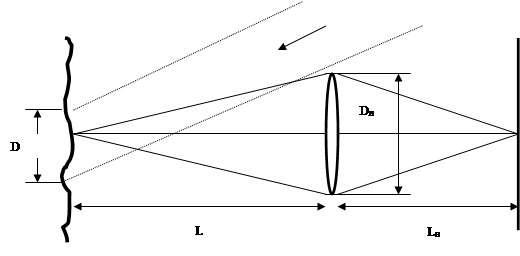Рис. 25.2.

Образование субъективной спекл-структуры:

D – диаметр засвеченной области на объекте, L – расстояние между объектом и оптической системой, D_л - световой диаметр оптической системы, L_н – расстояние от оптической системы до наблюдателя (экрана).

Совокупность методов, позволяющих получать информацию о рассеивающем объекте посредством изучения особенностей спекл-структуры, носит название спекл-интерферометрии. Как видно, для спекл-интерферометрии основной интерес представляет субъективная спекл-структура, тем более, что при визуальном наблюдении спекл-картины она автоматически субъективизируется оптической системой глаза.

В плоскости изображения распределение интенсивности вокруг геометро-оптического изображения точки описывается, как известно, функцией Эйри:

Ф ( r ) =½ 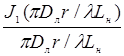½ (25.2)

Радиус r₀ первого светлого кольца соответствует первому нулю функции Бесселя J₁ ,достигаемому при значении аргумента, равном приблизительно 3,83. Отсюда 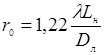, т.е. известная формула для предельного разрешения оптической системы согласно критерию Рэлея. Эта величина и будет определять поперечный размер спекла для субъективной спекл-картины:

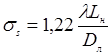(25.3)

Видно, что в субъективной спекл-картине вместо диаметра пятна засветки фигурирует диаметр линзы, а вместо расстояния от облучаемой поверхности до наблюдателя – расстояние от линзы до плоскости изображения. Полезно связать характерный размер спекла с фокусным расстоянием или, что аналогично, с увеличением системы. Вводя увеличение b , запишем:

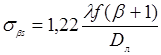(25.4)

Формирование в плоскости изображения картины спеклов, имеющих размер s_bs, эквивалентно тому, что сама рассеивающая поверхность как бы покрыта спеклами, имеющими размер

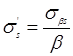(25.5)

Не менее важной характеристикой спекл-картины является продольный размер спеклов. К оценке размера спекла вдоль оптической оси приводят следующие соображения. Пусть в точке Р₀ экрана наблюдается максимум интенсивности. Это означает, что колебания от различных точек освещенной поверхности усиливают друг друга. Рассмотрим освещенную область D_л как источник вторичных волн Гюйгенса-Френеля (см. рис. 25.3).

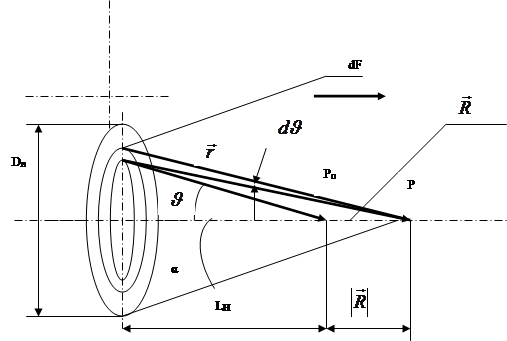Рис.25.3.