Спонтанное и вынужденное излучение.
Из принципов квантовой механики следует, что микросистемы (молекулы, атомы, ионы и т.д., в дальнейшем будем объединять их понятием «активные центры») могут находиться в определенных квантовых состояниях (на определенных энергетических уровнях), характеризующихся дискретными значениями энергии. Переходы между этими состояниями сопровождаются поглощением или выделением энергии. При переходе в состояние с меньшей энергией активные центры выделяют энергию; для того, чтобы перейти в состояние с большей энергией, активные центры должны поглотить энергию. Подобные переходы могут происходить либо с испусканием (поглощением) кванта энергии в виде фотона, либо безызлучательно ― в результате взаимодействия с другими частицами (соударение атомов в электрическом разряде, обмен энергией с кристаллической решеткой и т.д.).
Переходы между энергетическими уровнями изолированных активных центров носят излучательный характер. Энергия при таких переходах (рисунок 2.1) излучается (поглощается) в виде кванта электромагнитного поля, частота n колебаний которого связана с энергиями уровней Е1 и Е2 известным соотношением:
h n = Е2 – Е1, (2.1)
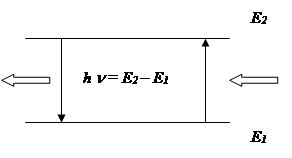 где h –постоянная Планка(h= 6,6256 10-27эрг с).
где h –постоянная Планка(h= 6,6256 10-27эрг с).
Рисунок 2.1. Модель резонансного взаимодействия между внешним электромагнитным полем и двухуровневым активным центром
Рассмотрим ансамбль большого количества активных центров, которые могут находиться в состояниях с энергиями Е1 и Е2. Для характеристики такой системы введем понятие «плотность населенности» или просто «населенность уровня» ni, обозначающее число активных центров в единице объема, находящихся на определенном (i-м) энергетическом уровне. При термодинамическом равновесии соотношение населенностей двух уровней подчиняется закону Больцмана:
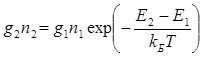 (2.2)
(2.2)
 |
где kБ – постоянная Больцмана (индекс Б использован, чтобы не путать ее с волновым числом, также часто встречающимся в формулах), Т ― абсолютная температура, g1 и g2 ― факторы вырождения или статистические веса уровней, которые показывают, сколько независимых состояний активного центра могут иметь одну и ту же энергию (в дальнейшем будем полагать g1 и g2равными единице).
Фактическое число энергетических состояний любой микросистемы бесконечно, и закону Больцмана подчиняется вся совокупность населенностей энергетических уровней. Выделение только двух из них связано с резонансным взаимодействием среды и внешнего электромагнитного поля.
Активный центр, находящийся на верхнем («возбужденном») энергетическом уровне может перейти в нижнее энергетическое состояние самопроизвольно («спонтанно»), т.е. без влияния внешнего поля. Сопровождающее такой переход излучение называется соответственно спонтанным.
 |
Здесь необходимо выделить явление, приводящее к первому принципу, лежащему в основе работы лазеров. Это ─ индуцированное (вынужденное) излучение, существование которого постулировано А. Эйнштейном в 1916 г. [1].
Дело в том, что за счет только спонтанного излучения при переходе из возбужденного состояние в менее возбужденное невозможно объяснить процесс установления термодинамического равновесия между веществом и излучением. В самом деле, согласно распределению Больцмана, населенность верхнего уровня в равновесном состоянии всегда меньше, чем населенность нижнего. Следовательно, при наличии только спонтанного излучения вся энергия с необходимостью должна перетекать в среду, что противоречит самому предположению о наличии термодинамического равновесия. Ситуация напоминает «ультрафиолетовую катастрофу» в теории теплового излучения, только наоборот. Получилось, что, разрешив проблему теплового излучения посредством введения квантов, Планк создал новую, не менее актуальную. Для ее разрешения необходимо рассмотреть процессы, происходящие под действием электромагнитного излучения, резонансного рассматриваемому переходу.
Эйнштейн предположил, что вероятность вынужденного перехода между состояниями пропорциональна спектральной плотности r энергии вынуждающего (резонансного данному переходу) излучения. Плотность энергии электромагнитного излучения в интервале частот n, n+dn определяется через спектральную плотность по формуле r = rn dn.
Таким образом, в ансамбле квантовых частиц, обладающих дискретными уровнями энергии, существует три типа переходов между двумя заданными энергетическими состояниями Е1 и Е2 (см. рисунок 2.2).:
а) спонтанные переходы сверху вниз с излучением кванта энергии:
hn = Е2 – Е1;
б) переходы сверху вниз, индуцированные внешним электромагнитным полем:
Е2 ® Е1 — индуцированное излучение;
в)переходы снизу вверх, происходящие с поглощением кванта энергии от внешнего поля:
Е1 ® Е2 — поглощение.
 |
Строго говоря, необходимо учитывать и безызлучательные (релаксационные) переходы, происходящие за счет взаимодействия активных центров между собой и с окружающей средой. Но эти переходы, приводящие к установлению термодинамического равновесия в самой среде и описывающие превращение энергии излучения в другие формы (тепловую, химическую, механическую и т.п.) мы при рассмотрении баланса вещество-излучение можем пока опустить.
Ансамбль активных центров, находящийся при температуре Т в состоянии термодинамического равновесия, должен быть в равновесии с полем его собственного электромагнитного излучения, испускаемого и поглощаемого при переходах между уровнями 1 и 2. При термодинамическом равновесии весь ансамбль (вещество + излучение) не теряет и не приобретает энергии. Значит, за единицу времени общее число переходов 2®1 должно быть равно общему числу переходов 1®2. Это число определяется населенностью уровней n1 и n2. Равновесное распределение населенностей по уровням определяется формулой Больцмана (2.2).
Полное число переходов 2®1 равно произведению населенности n2 на вероятность W21 перехода 2®1 для одной частицы. Для спонтанных переходов:
dWспонт = А21dt (2.3)
где А21 — коэффициент Эйнштейна, определяемый как вероятность спонтанного перехода 2®1 в единицу времени. Поскольку самопроизвольных переходов атома вверх не бывает, заселение верхнего уровня возможно только вынужденным путем под действием электромагнитного поля. Пусть плотность энергии этого поля в единичном спектральном интервале составляет rn. Тогда в равновесии будет:
В12·rn exp(–Е1 /kБТ) = (В21rn + А21) exp(–Е2 /kБТ) (2.4)
Здесь В12 и В21 — вероятности индуцированных поглощения и излучения в единицу времени соответственно, называемые коэффициентами Эйнштейна. Из (2.4) выразим плотность энергии rn :
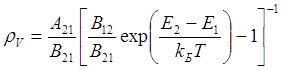 (2.5)
(2.5)
Поскольку при Т ® ¥ спектральная плотность излучения rn должна неограниченно возрастать, получим, полагая знаменатель в выражении (2.5) равным 0:
В12 = В21. (2.6)
В случае невырожденных уровней (g1≠g2≠1) имеем g1В12 = g2В21
То есть: вероятности вынужденных переходов с испусканием и поглощением излучения равны друг другу с точностью до коэффициентов вырождения.
В замкнутой полости, в которой поглощаются и испускаются электромагнитные волны, в условиях статистического равновесия спектральная плотность излучения rn определяется формулой Планка:
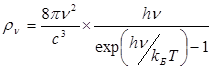 (2.7)
(2.7)
Здесь с — скорость света.
Используя условие hn = Е2—Е1, получим из (2.5) и (2.7) выражение, связывающее величины вероятностей вынужденных и спонтанных переходов :
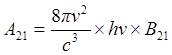 (2.8)
(2.8)
Выражение (2.8) связывает между собой вероятности, казалось бы, принципиально различных процессов, однако из него следует, что всякий спонтанный переход 2®1 влечет за собой и индуцированные переходы между этими состояниями, причем возрастание плотности энергии приводит к возрастанию роли индуцированного излучения:
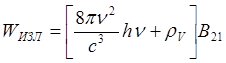 (2.9)
(2.9)
При 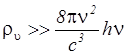 , (т.е.
, (т.е. 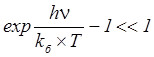 )
) 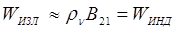
Итак, первый принцип, лежащий в основе работы лазеров, заключается в том, что вероятность переходов, связанных с вынужденным поглощением или испусканием света, пропорциональна плотности энергии резонансного излучения.
 |
Индуцированное излучение, в отличие от спонтанного, допускает классическую аналогию. Представим себе гармонический осциллятор, находящийся в поле внешней силы. При резонансном характере этой внешней силы осциллятор получает энергию от внешней силы и раскачивается. Это, в общем, тривиально. Нетривиально то, что при определенном фазовом соотношении между исходными свободными колебаниями осциллятора и внешней силой осциллятор может не поглощать энергию от внешнего поля, а, наоборот, отдавать ее полю. Это и есть индуцированное излучение, которое по смыслу своему когерентно, т.е. сохраняет фазовые соотношения с внешним полем (при их несохранении передача энергии от осциллятора к полю невозможна).
Взаимодействие, подобное описанному, можно рассматривать только при формировании ансамбля осцилляторов, группирующихся под действием внешнего поля. Это справедливо при условии, что расстояния между осцилляторами сравнимы с длиной волны (только в этом случае можно организовать противофазные колебания осциллятора и внешнего поля). В квантовой же системе это условие вовсе не обязано выполняться, более того, расстояние между частицами, как правило, мало по сравнению с длиной волны. В силу соотношения неопределенностей DN ´ Dj ³ 1/2 фаза электромагнитной волны j определена только тогда, когда мы вообще не знаем, сколько квантов N в этой волне содержится. Поэтому бессмысленно говорить о фазе отдельного кванта.
Тогда как же понимать когерентность индуцированного излучения?
Заметим, что если для двух волн известна разность фаз (а не значения индивидуальных фаз), то соотношение неопределенностей разрешает определение полного числа квантов, оставляя неопределенной их принадлежность к данной из двух волн. Поэтому при сложении в одну волну когерентных электромагнитных излучений, соответствующих нескольким квантам, мы говорим о сложении неразличимых квантов. Но кванты электромагнитного поля — фотоны — подчиняются статистике Бозе-Эйнштейна, по которой число квантов, приходящихся на один осциллятор поля (иначе: один тип колебаний или одну моду), не ограничено. В силу полученного выше соотношения (1.9), с ростом числа фотонов возрастает и вероятность их испускания в единицу времени, а ввиду их тождественности фаза, частота и все прочие характеристики остаются неизменными.
Из соотношения (2.9) следует и пересмотр понятия «спонтанное излучение» с той точки зрения, что оно не может быть полностью «самопроизвольным». Поскольку в квантовом представлении осциллятор поля характеризуется ненулевой энергией даже в отсутствие фотонов (при N = 0 энергия гармонического осциллятора равна 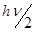 и называется энергией нулевых колебаний), спонтанное излучение можно рассматривать как результат взаимодействия возбужденного активного центра с нулевыми колебаниями поля.
и называется энергией нулевых колебаний), спонтанное излучение можно рассматривать как результат взаимодействия возбужденного активного центра с нулевыми колебаниями поля.
Напомним, что при записи соотношений, связывающих вероятности спонтанного и индуцированного излучения, не учитывались релаксационные переходы, связанные с необратимыми превращениями поглощенной энергии. В отсутствие внешнего электромагнитного поля сообщенная системе энергия с релаксирует с некоторой постоянной времени t, большой по сравнению с периодом колебаний поглощенного электромагнитного поля. Именно релаксационные процессы создают равновесное распределение и условия для продолжения процессов излучения и поглощения. Эти процессы должны учитываться при строгом рассмотрении (см. ниже).
Дата добавления: 2017-01-26; просмотров: 3072;











