Положительная обратная связь. Оптический резонатор.

В мазерах таким устройством стали традиционные объемные резонаторы [3,4]. В лазерах используется еще более простое решение, предложенное впервые А.М. Прохоровым в 1956 г.[8] ― активная среда располагается между двумя зеркалами, возвращающими излучение в зону усиления. В отличие от СВЧ резонаторов, представляющих замкнутые объемы с проводящими стенками, такие резонаторы называют открытыми (рисунок 2.5).

Рисунок 2.5. Схема лазера с резонатором Фабри-Перо.

В простейшем виде открытый резонатор типа Фабри-Перо представляет собой две плоскопараллельные отражающие пластины, или зеркала, находящиеся на некотором расстоянии l >> l друг от друга (l— длина волны излучения, соответствующего рабочему переходу hn = Е₂―Е₁). Форма зеркал не очень существенна, если иметь в виду, что их размер также велик по сравнению с l. Отражение одного из зеркал («глухого») делается по возможности более близким к 1, второе (выходное) делается частично попускающим излучение рабочего перехода.

Если расстояние l таково, что между зеркалами укладывается целое число полуволн, то в пространстве между зеркалами возникает стоячая волна. Это, собственно, и есть то, что позволяет употреблять слово «резонатор». Пренебрегая потерями энергии в пространстве между зеркалами, все потери можно связать с излучением через зеркала во внешнее пространство. Из теории колебаний известно, что потери определяют важнейшую характеристику резонатора как колебательной системы, а именно добротность. По определению добротность есть:

Q = 2p ´ (Е/DЕ_пер) (2.16)

где Е — энергия, накопленная в системе, DЕ_пер — потери энергии за период.

При наличии стоячей волны в резонаторе, имеющем энергетический коэффициент отражения от зеркал R, можно оценить добротность из элементарных соображений. Стоячая волна, как известно, эквивалентна двум бегущим волнам равной интенсивности, распространяющимся в противоположных направлениях. Пусть поток энергии в каждой из этих волн равен Р. При отражении от двух одинаковых зеркал теряется мощность 2P(1 — R), а накопленная в резонаторе энергия составляет Е = 2Рt = 2Рl/c (t — время однократного пробега волны между зеркалами). Подставляя эти выражения в формулу (2.16), получим:

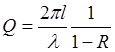(2.17)

где учтено, что l = сТ ( Т — время одного периода световых колебаний).

Формула (2.17) работает тем лучше, чем ближе R к единице, причем при 1— R << 1 значение Q для открытого резонатора может быть очень велико. Но она записана для «пустого» резонатора, то есть без учета свойств среды в пространстве между зеркалами. Чтобы учесть их, обратимся к оптике, где подробно исследуется аналогичная колебательная система, рассматриваемая не как резонатор, а как интерферометр Фабри-Перо (см., например, [9]). Величина, аналогичная добротности, называется при этом разрешающей силой и записывается так:

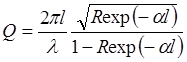(2.18)

Здесь a — показатель поглощения света средой, заполняющей пространство между зеркалами. В нашем случае вместо поглощения a следует поставить усиление (2.15), и тогда добротность «активного», т.е. заполненного усиливающей средой, интерферометра Фабри-Перо будет равна:

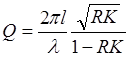(2.19)

где К = exp(α₀ ´ l) — коэффициент усиления активной среды за проход.

Формула (2.19), очевидно, теряет смысл при RK=1. Но именно это условие соответствует равенству энергии, приобретаемой за счет усиления в активной среде и теряемой при излучении в окружающее пространство.

Если RK<1, мы имеем усилитель с положительной обратной связью (регенерированный усилитель) При RK=1 усилитель самовозбуждается и превращается в генератор. Смысл условия самовозбуждения прост: потери энергии за проход должны быть скомпенсированы усилением за этот же проход.

Заметим, что проведенное рассуждение справедливо только для симметричного резонатора, то есть такого, у которого зеркала одинаковы и имеют совпадающие коэффициенты отражения R. Для несимметричного резонатора, у которого одно зеркало глухое (R=1), а другое (выходное) имеет коэффициент отражения R<1, потери на выходном зеркале должны компенсироваться не однократным, а двукратным прохождением расстояния между зеркалами, и условие генерации запишется так: RK² = 1

Можно в принципе предложить много различных схем сочетания системы зеркал с активной средой и для каждой из них получить свое условие возбуждения. Общее же требование на это условие гласит: усиление в активной среде за некоторый (эффективный) проход излучения через систему зеркал резонатора и активную среду должно скомпенсировать все потери энергии в резонаторе за этот же эффективный проход:

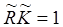(2.20)

Здесь 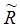означает все потери (как на выход излучения наружу, так и на рассеяние, поглощение элементами внутри резонатора и т.п.).

Отметим важное обстоятельство, принципиальное для выполнения условия (2.20) в обобщенном смысле. Понимая (2.20) как условие на комплексные величины 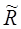и 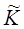, следует разбивать условие самовозбуждения на баланс амплитуд и баланс фаз. Резонансные условия выполняются для излучения той частоты, для которой реализуется стоячая волна, то есть все фазовые набеги взаимно компенсируются. Поэтому если баланс амплитуд позволяет вычислить выходную мощность лазера, то баланс фаз дает значение частоты.

Таким образом, в основе работы лазеров лежат три принципа:

1. Наличие вынужденного излучения, заключающееся в том, что вероятность переходов между энергетическими уровнями в активной среде, связанных с поглощением и испусканием излучения, пропорциональна спектральной плотности резонансного излучения.

2. Явление вынужденного излучения может быть использовано для усиления электромагнитного излучения, если для пары уровней в активной среде создана инверсная населенность, т.е. состояние, при котором населенность на верхнем уровне превосходит населенность на нижнем уровне.

3. Для обеспечения режима генерации необходимо активную среду, усиливающую излучение поместить в резонатор, т.е. устройство, обеспечивающее положительную обратную связь.

ЛИТЕРАТУРА к лекции 2.

1. Эйнштейн А. Собрание научных трудов в 4 томах, т.3. ― М., Наука, 1966.

2. Фабрикант В.А. // Труды ВЭИ, 1940, вып.1, 236.

3. Басов Н.Г., Прохоров А.М. // ДАН СССР, 1955, 101, № 1, 47.

4. Gordon J.P., Zeiger H.J., Townes C.H. // Phys. Rew., 1955, 99, 1264.

5. Lamb W.E., Jr. // Phys. Rew., 1964, 134, 1429.

6. Юдин В.И. // Кв. электр., 1979, 6, №7, 1559.

7. Конюхов В.К., Прохоров А.М. // Письма ЖЭТФ, 1966, 3, № 11, 436.

8. Кац М.Л., Ковнер М.А., Сидоров Н.К. Оптические квантовые генераторы. ― Саратов, Изд. СГУ, 1964.

9. Сивухин Д.В. Общий курс физики, т.4. Оптика. ― М., Наука, 1980.

10. Карлов Н.В. Лекции по квантовой электронике.― М., Наука, 1983.

11. Микаэлян А.Л., Тер-Микаелян М.Л., Турков Ю.Г. Оптические квантовые генераторы на твердом теле. ― М., Сов. радио, 1967.