Методика ОГТ. Обработка и интерпретация данных ОГТ.

Годограф ОГТ.

Система ОГТ предполагает, что регистрация отраженных волн (ОВ) осуществляется в точках приема х₁, х₂, х₃ и т.д, расположенных по отношению к источникам О₁, О₂, О₃ и т.д. так, как если бы граница R залегала горизонтально и выполнялась бы схема распространения волны от общей точки R_огт, находящейся на этой границе( Рис .59).

Рис.59.Схема лучей при получении годографа ОГТ.

Рис.60.Годографы ОГТ: а-в случае с наклонной отражающей границы; б-при разных углах наклона φ отражающей границы.

Годограф ОГТ определяет времена ОВ, приходящих в эти точки, и является составным, так как для его получения используются времена прихода волн, возбужденных в разных ПВ. Годограф ОГТ можно вывести из годографа ОТВ, если перейти в новую систему координат, где началом будет точка ЦБ (центр базы) расположенная на середине расстояния между источником O и приемником S (рис.60).

Уравнение годографа ОВ в системе ОТВ записывается, как мы помним, в виде

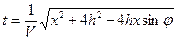
Если положить h= h₀+ 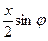, где h₀ – глубина границы по нормали под точкой ЦБ (новым началом координат), то

.

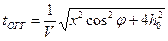Из рисунка видно, что данное выражение получено для двухслойной модели среды. Исследование показывает, что в этом случае годограф ОГТ – t_ОГТ представляет собой гиперболу, симметричную относительно оси времени t, с минимумом над точкой ЦБ. Эта гипербола будет всегда симметричной относительно оси t, а кривизна ее зависит только от угла φ, и не зависит от знака угла. С увеличением φ гипербола выполаживается( Рис.60б).

Обозначим 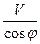через V_ОГТ. Перепишем с учетом этого уравнение годографа t_ОГТ в виде .

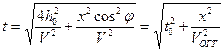Получили уравнение, аналогичное уравнению обычного продольного годографа однократной ОВ в системе ОТВ для двухслойной среды с φ=0 (границы горизонтальна), но параметр его уже не V, а V_ОГТ – фиктивная скорость, зависящая от φ и стремящаяся к ∞, когда φ → 90º и равная скорости V в однородной среде, если граница горизонтальна. Таким образом, для аппроксимации наблюденного годографа ОГТ (в многослойной среде) гиперболой необходимо подобрать удовлетворяющее данному t₀ значение V_ОГТ, определяемое как 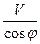, то есть осуществить выбор подходящей теоретической гиперболы. При наклонном залегании условие отражения от общей точки не выполняется. Точка расползается на площадку, залегающую под углом φ, отражения от которой условно приписывают точке О´ - проекции ЦБ на нормаль к границе. Длина площадки ΔL, как показывают специальные исследования, равна

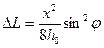. При φ<10º отношение х /h₀<0,5, а длина площадки ΔL не превышает 0,05 от длины базы возбуждение-прием.