Основной закон, определяющий величину тока, протекающего через проводник (горную породу) – закон Ома

J = 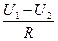, где U₁ и U₂ значения потенциала на концах проводника, а R – его сопротивление R=ρ 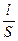и, соответственно, ΔU = JR= Jρ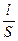

Здесь l – длина проводника в м, S – площадь его поперечного сечения в м², а ρ – удельное сопротивление, измеряемое в омах, умноженных на метр (ом·м). Величина, обратная ρ называется удельной электрической проводимостью и измеряется в сименсах

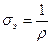
Наряду с силой тока, одной из характеристик поля является плотность тока j

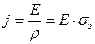
Это так называемая дифференциальная форма записи закона Ома, устанавливающая пропорциональность плотности тока в проводнике напряженности поля. Эта форма записи может быть применена к проводникам любой формы и к переменным электромагнитным полям. Поле постоянного электрического тока в однородном полупространстве (ρ = const) называют нормальным электрическим полем постоянного тока.

Рассмотрим нормальное поле точечного источника. Получить такое поле, пропуская ток через пару электродов А и В можно, относя второй электрод в бесконечность и анализируя ситуацию в окрестности А. В однородной среде ток от точечного источника стекает во все стороны равномерно. Эквипотенциальные поверхности (поверхности равного потенциала) перпендикулярны к радиальным токовым линиям и имеют форму полусфер с центром в точке А ( рис.22 )

Рис.22.Нормальное поле одного (а) и двух разнополярных (б) точечных электродов

1 – токовые линии; 2 – эквипотенциальные поверхности.

Определим значение потенциала U_м в точке М.

Вначале оценим величину разности потенциалов между двумя близкими эквипотенциальными поверхностями радиусов r и r+dr. Начало координат поместим в точку А. Согласно закону Ома

dV=JdR=J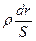

Здесь dr – длина проводника - в данном случае расстояние между соседними полусферами, S - это поверхность полусферы, то есть 2πr², где r – радиус полусферы. Поскольку рассматриваются две полусферы, отстоящие друг от друга на dr – правильнее всего выбрать радиус равным r + dr/2 – то есть выбрать некий «средний» радиус близких полусфер

Тогда dV=

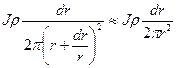
Приближенное равенство основано на том, что бесконечно малая dr и при возведении в квадрат и при умножении на конечную величину r дает в результате столь малые «добавки» к r² , что ими вполне можно пренебречь.

Для нахождения U_м придется просуммировать согласно определению потенциала все dV от бесконечности до r, то есть проинтегрировать приведенное выражение, сложив тем самым приращения потенциала dV всех подобных рассмотренному тонких слоев, вынеся постоянные – силу тока в источнике, удельное сопротивление среды и 2π – за знак интеграла

H_M=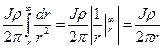

Исходя из этого, напряженность поля в М

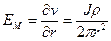
А плотность тока

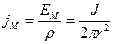
Получив основные характеристики нормального поля точечного электрода обратимся к рассмотрению реальной ситуации, когда поле создано с помощью пары электродов АВ (рис.22б), а регистрация осуществляется парой МN. Тогда разность потенциалов

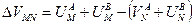
Обозначив расстояние АМ через r₁ и AN через r₂ можем, учитывая симметрию четырехэлектродной расстановки AMNB относительно центра 0, записать

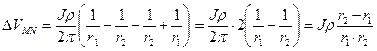
Учитывая, что r₂ – r₁ равно расстоянию MN

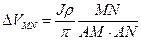, обозначив π 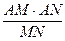через k,

откуда 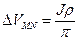, а .

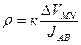k – это коэффициент, характеризующий геометрию расстановки.

Вполне понятно, что если среда однородная, то есть ρ = const, мы будем получать одно и то же значение ρ при любых k, то есть при любых расстояниях АМ и AN.

Однако, в неоднородной среде ρ будет существенно зависеть от k. Эта зависимость обусловлено тем, что плотность тока определяется величиной «разноса» питающих электродов АВ и с увеличением АВ эта относительная плотность с глубиной возрастает, поскольку возрастает и глубина проникновения поля в Землю. Сказанное хорошо видно из рассмотрения такого примера ( рис.23 ).

Пусть мы имеем толщу слоев с разным сопротивлением.

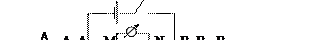
Рис.23.Зависимость глубины проникновения электрического поля в слоистую среду от величины разноса питающих электродов АВ.

При малом разносе АВ токовые линии практически целиком размещаются в слое с сопротивлением ρ₁. При большем разносе А₁В₁ поле сосредоточено больше й частью в слое ρ₂, здесь плотность тока, отображаемая густотой силовых линий будет наибольшей. С увеличением АВ до А₁В₁ вычисляемое по приведенной формуле ρ будет уже ближе всего к ρ₃ и т.п.

В теории электроразведки показано, что отношение тока на глубине h к плотности на поверхности зависит от расстояния между электродами L и при увеличении L эта относительная плотность с глубиной h возрастает по закону

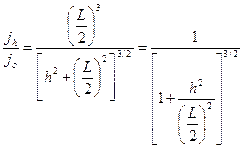
Все сказанное позволяет уяснить идею зондирования среды постоянным током, состоящую в том, что осуществляя серию измерений ΔV_MN с разными все возрастающими АВ, мы получаем последовательность значений ρ, характеризующих электрическое сопротивление все более глубоких интервалов геоэлектрического разреза. Такое зондирование называют вертикальным электрическим зондированием ВЭЗ. Помимо ВЭЗ используют другие модификации рассматриваемого метода сопротивлений – ДЭЗ (дипольное электрическое зондирование), ЭП (электропрофилирование) и другие. Во всех этих модификациях основная задача – определение электрической характеристики среды – удельного электрического сопротивления ρ. Однако, что это за ρ? Это в общем случае не ρ₁, не ρ₂ и не ρ₃, а некое ρ_к – кажущееся сопротивление, зависящее от k (то есть от геометрии 4^хэлектродной установки ABMN - от расстояний АВ и MN.), помимо зависимости от этих реальных ρ₁ , ρ₂ и от толщин слоев геоэлектрического разреза. Таким образом, ρ_к можно определить как удельное электрическое сопротивление такой воображаемой однородной среды, в которой при тех же АВ и MN и при той же силе питающего тока в цепи АВ регистрируется та же разность потенциалов ΔV_MN , что и в среде неоднородной. То есть ρ_к это сложная функция, зависящая от характеристик реального геоэлектрического разреза и от геометрии расстановки

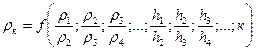
Самое замечательное состоит в том, что в ряде случаев ρ_к может оказаться как угодно близким к истинным значениям ρ_{1 ,} ρ₂ и т.д. Но это будет показано несколько позже. А пока остановимся на рассмотрении упомянутых модификаций и сделаем это несколько подробнее, чем по ранее представленным методам электроразведки. Но прежде одно замечание, которое должно прояснить читателю, почему и теория методов сопротивлений на постоянном токе и практика их применения разъясняются гораздо обстоятельней, чем это делалось ранее в разделах, посвященных МТЗ и пр.. Дело в том, что эти методы занимают особое место среди других методов электроразведки и геофизики в целом. Во-первых, с методики ВЭЗ и каротажа КС (кажущихся сопротивлений) началась в первой трети двадцатого столетия разведочная геофизика как таковая. Во-вторых, эти методики используются в современной геофизике чаще, чем какой-либо другой метод практически во всех разновидностях полевой геофизики (инженерная, рудная, гидрогеологическая, техническая, археологическая и пр.), за исключением нефтегазовой, хотя история нефтегазовой геофизики тоже ведет свой отсчет именно с этих методик.

Наиболее популярны две разновидности метода сопротивлений: ВЭЗ и электропрофилирование. Для электроразведочных методов вообще характерно такое подразделение - зондирование и профилирование. Зондирования предназначены, главным образом, для исследования горизонтально-слоистых сред, представляющих, в основном, осадочные толщи, а профилирование – для выявления вертикальных или крутонаклоненных неоднородностей, свойственных разрезам с блоковой тектоникой. Сочетание зондирований с профилированием позволяет получить всестороннее объемное представление о строении объектов самой разной природы.