Применение метода симметричных составляющих

На практике встречаются случаи, когда отдельные фазы трансформатора нагружены несимметрично (неравномерное распределение осветительной нагрузки по фазам, подключение мощных однофазных приемников и т.д.). Кроме того, в электрических сетях, питающихся от трансформаторов, случаются несимметричные короткие замыкания (однофазные на землю или на нулевой провод и двухфазные). При анализе несимметричных режимов работы трансформатора будем предполагать, что сам трансформатор имеет симметричное устройство, то есть все три фазы одинаковы в магнитном и электрическом отношениях.

Общим методом анализа несимметричных режимов является метод симметричных составляющих.

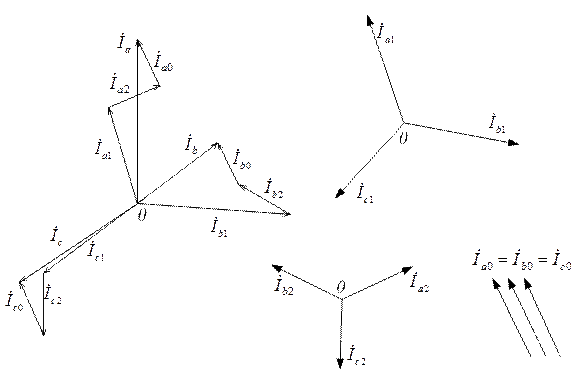
Рис. 2.7. Симметричные составляющие трехфазных токов

Согласно этому методу, трехфазная несимметричная система токов 1_а , I_b , I_c разлагается на три системы токов прямой (I_a1 , I_b1 , I_c1), обратной (I_a2 , I_b2 , I_c2) и нулевой (I_a0 , I_b0 , I_c0) последовательности (рис. 2.7), связанные соотношениями

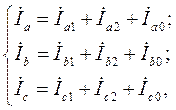(2.21)

где

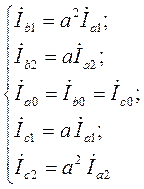(2.22)

и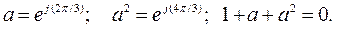

Симметричные составляющие фазы a, которые обычно принимаются за основные, определяются выражениями

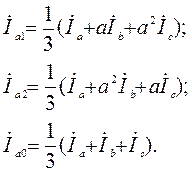(2.23)

Заметим, что аналогичные соотношения действительны также для несимметричной системы напряжений фаз U_a , U_b, U_c и их симметричных составляющих.

Применение метода симметричных составляющих основано на принципе наложения. Тем самым предполагается, что для всех участков магнитной цепи трансформатора μ = const, чем и обусловлена возможность его применения.

В целях упрощения записей далее будем предполагать, что число витков в первичной и вторичной обмотках равно (ω₁ = ω₂) и поэтому нет надобности различать приведенные и неприведенные вторичные величины и обозначать последние штрихами. Общность получаемых при этом результатов не нарушается, так как всегда можно выполнить соответствующие пересчеты. Первичные фазные величины будем обозначать индексами А, В, С, а вторичные – индексами а, b, с.