Подобие процессов конвективного теплообмена

При аналитическом расчёте коэффициента теплопередачи основной проблемой является определение коэффициента теплоотдачи, как со стороны горячего, так и со стороны холодного теплоносителей. Как известно, коэффициент теплоотдачи зависит от большого числа параметров и, следовательно, его значения невозможно привести в виде таблиц или графиков. Интенсивность конвективного теплообмена зависит от условий между стенкой и средой, от теплопроводности ламинарного пограничного слоя, от условия движения среды, поэтому этот процесс описывается системой дифференциальных уравнений. С помощью которых, в принципе, можно решить задачу конвективного теплообмена, но до настоящего времени такого решения не существует. В этих условиях большое значение приобретают экспериментальные исследования, однако проводить эксперименты для бесчисленного множества процессов теплообмена считается трудоёмкой задачей, которая также невыполнима.

Таким образом, ни теоретические, ни экспериментальные методы не дают полного решения задачи – конвективного теплообмена. С целью решения данной задачи была разработана теория подобия, которая позволяет бесчисленное множество процессов теплообмена разделить на конечное число групп подобных явлений. Для каждой группы подобных явлений достаточно провести одну серию экспериментальных исследований. Результаты этих экспериментов обрабатываются методом теории подобия.

Если систему дифференциальных уравнений обработать методом теории подобия, то получится следующий общий вид критериального уравнения:

Nu=f(Re, Gr,Pr), (9.1)

Nu– число Нуссельта, характеризующее конвективный теплообмен между жидкостью и поверхностью твёрдого тела,

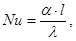(9.2)

где α– коэффициент теплоотдачи, Вт/(м²∙К);

l – определяющий геометрический размер, м;

λ– коэффициент теплопроводности теплоносителя, Вт/(м∙К);

Re– число Рейнольдса, характеризующее отношение сил инерции к силам вязкости и определяющее характер течения жидкости,

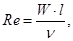(9.3)

где W – средняя скорость теплоносителя, м/с;

v – коэффициент кинематической вязкости, м²/с;

Gr– число Грасгофа, характеризующее движение при естественной конвекции и показывающее соотношение подъемной силы, возникающей вследствие разности плотностей жидкости и сил молекулярного трения,

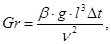(9.4)

где β=1/Т – температурный коэффициент объемного расширения, 1/К;

Т – температура среды, K;

g– ускорение свободного падения, м/с²;

Δt– разность температур между стенкой и омывающей средой;

Pr– число Прандтля, определяющее физические свойства жидкости,

Pr 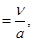(9.5)

где а– коэффициент температуропроводности, м²/с.