Динамические характеристики элементов автоматики

ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИКИ, ЭЛЕМЕНТЫ АНАЛИЗА И СИНТЕЗА СИСТЕМ УПРАВЛЕНИЯ

Общие представления об элементах автоматики.

Для удобства проектирования, анализа и синтеза систем автоматического управления, на практике применяют типовые виды элементарных звеньев, имеющие определенные динамические параметры. Данные звенья соединяют в требуемую структурную схему, и в зависимости от их характеристик получают необходимые выходные параметры системы. Характеристиками звеньев являются дифференциальные уравнения, описывающие изменения, происходящие в звене во время переходного процесса. Характеристикой системы будет являться совокупность дифференциальных уравнений, описывающих поведение системы во время переходного процесса.

Независимо от сложности, из элементарных звеньев можно составить схему практически любой системы автоматического управления. Данные звенья и их характеристики были подробно рассмотрены в 1 разделе.

Возьмем некоторый элемент системы, который приближенно представим в виде устройства с одним входом и одним выходом (рисунок 42).

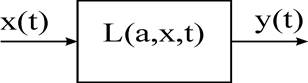
Рис.42. Условный элемент САУ

Данный элемент имеет определенные параметры, например, а – параметр элемента, определяющий его характеристику и функциональное назначение. Входная и выходная величины параметра элемента взаимосвязаны и их зависимость может быть математически представлена в виде:

у(t)=L(a,x,t)x(t) (2.1.)

Элемент автоматики, как и ранее рассмотренные звенья систем автоматического управления, может быть охарактеризован с точки зрения статики и динамики. Эти характеристики влияют не только на процессы, происходящие собственно в элементе, но и на процессы, происходящие при выполнении задачи управления целиком в системе.

Динамические характеристики элементов автоматики

Динамическими характеристиками элемента определяется его инерционность (время переходного процесса), изменение параметров элемента во время нагрузки, максимальное отклонение величины регулируемого параметра. К этим характеристикам относятся:

- постоянная времени,

- перерегулирование,

- полоса пропускания.

Элементы автоматики также могут подразделяться на инерционные и безынерционные. Примерами безынерционных элементов могут служить жесткие связи, передающие величины физических параметров без задержек по времени, т.е. переходной процесс к установившемуся состоянию отсутствует. Инерционные элементы – такие элементы, у которых переходной процесс от одного установившегося состояния к другому установившемуся состоянию имеет место. Для наглядности и упрощения расчетов чаще всего используют реакцию элемента на единичное ступенчатое воздействие или дельта-функцию. Графическое представление характеристик переходных процессов в элементах автоматики показано на рисунке 43.

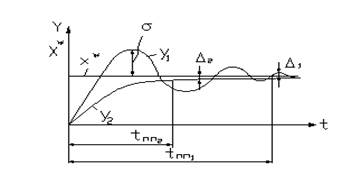
Рис.43. Графики динамических характеристик переходных процессов элементов

автоматики

На графике изображены:

У₁ – характеристика переходного процесса колебательного звена,

У₂ – характеристика переходного процесса апериодического звена,

t_пп1 – время переходного процесса в колебательном звене,

t_пп2 – время переходного процесса в апериодическом звене.

Существует зона допустимых отклонений, которая представляет собой полосу пропускания не более 5% отклонения от установившегося значения. Переходной процесс считается завершенным, если значение выходного параметра попадает в указанную полосу.

Максимальное отклонение регулируемой величины параметра от номинальной величины параметра называется величиной перерегулирования, обозначается s, и является одной из основных величин, характеризующих переходной процесс в колебательном звене. Например, для необратимого процесса, у привода подачи металлообрабатывающего станка, sне превышает 10-15%. Для обратимого процесса, при использовании авиационных систем навигации, s может принимать значение до 30%.

От параметров элемента автоматики зависят все характеристики переходных процессов, протекающих в данном элементе. К данным параметрам относят:

α = 1 / Т - коэффициент демпфирования (затухания), где T является постоянной времени, w - собственная частота процесса преобразований, происходящих в элементе.

Переходной процесс в апериодическом звене математически представляется в следующем виде:

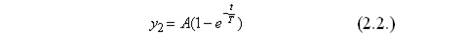
В данном случае A является установившимся значением выходной величины. Значение A будет равно значению входного воздействия при передаточном коэффициенте элемента равном 1.

Этим уравнением можно описать переходные процессы, протекающие в различных элементах, например, зарядка аккумулятора, установление температурного режима в печи при ее разогреве, и т.д. T – время перехода к установившемуся режиму, показатель инерционности. Переходной процесс в колебательном звене математически описывается в виде:

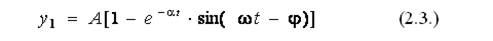
где w - собственная частота, a - коэффициент демпфирования, j - начальная фаза колебаний.