Оператор безусловного перехода goto

Возвращаясь к сказанному об операторе goto, необходимо отметить, что при всей его нежелательности все-таки существует ситуация, когда предпочтительно использовать именно этот оператор как с точки зрения структурированности текста программы, так и с точки зрения логики ее построения, и уж тем более с точки зрения уменьшения трудозатрат программиста. Эта ситуация - необходимость передачи управления изнутри нескольких вложенных циклов на самый верхний уровень.

Дело в том, что процедуры break и continue прерывают только один цикл - тот, в теле которого они содержатся. Поэтому в упомянутой выше ситуации пришлось бы заметно усложнить текст программы, вводя много дополнительных прерываний. А один оператор goto способен заменить их все.

Сравните, например, два программно-эквивалентных отрывка:

write('Матрица '); write('Матрица ');

for i:=1 to n do for i:=1 to n do

begin for j:=1 to m do

flag:=false; if a[i,j]>a[i,i]

for j:=1 to m do then begin

if a[i,j]>a[i,i] write('не ');

then begin flag:=true; goto 1;

write('не '); end;

break; 1: writeln('обладает

end свойством

if flag then break; диагонального

end; преобладания.');

writeln('обладает свойством

диагонального

преобладания.');

Программирование алгоритма циклической структуры

1. Задание: Вывод массива, удобный для пользователя. Распечатать двумерный массив размерности MxN удобным для пользователя способом. (Известно, что массив содержит только целые числа из промежутка [0..100].). Вычислите сумму элементов.

2. Алгоритм. Понятно что, если весь массив мы вытянем в одну строчку (или, того хуже, в один столбик), хороших слов в свой адрес мы не дождемся. Именно поэтому нам нужно вывести массив построчно, отражая его структуру.

3. В рабочей области редактора наберите код программы, представленный на листинге 1.

Листинг 1.

program Z1;

{$APPTYPE CONSOLE}

uses

SysUtils;

Const n=4;

m=5;

var a:array[1..n,1..m] of integer;

s,i,j:integer;

begin

{Ввод данных}

for i:= 1 to n do

for j:= 1 to m do

begin

Write(‘Vvedite element A[‘,i,’,’,j,’]: ’);

Readln(a[i,j]);

end;

{Печать результата}

Writeln;

Writeln('Matrix:');

for i:= 1 to n do

begin

for j:= 1 to m do

begin write(a[i,j]:4); s:=s+a[i,j] end;

writeln;

end;

Writeln('Summa=',s);

Writeln('End program.'); Readln;

end.

5. Запустите программу на решение и проверьте полученные результаты.

2.2 Программирование таблично заданной функции

1. Задание: Вычислить и вывести на печать значения функции y = a³ / (a² + x²) при значениях x, изменяющихся от 0 до 3 с шагом 0,1.

2. В программе заранее можно определить число повторений и использовать оператор цикла for.

3. Для оптимизации вычислительного процесса значения параметра a³ и a² вычислим вне цикла.

4. Наберите код программы, представленный на листинге 2.

Листинг 2.

program Z2;

{$APPTYPE CONSOLE}

uses

SysUtils;

var a,x,y,a2,a3:real;

i:integer;

begin

Write(‘Vvedite A=’);

Readln(a);

{Расчет и печать таблицы}

a2:=a*a; a3:=a*a*a;

x:=0;

Writeln;

Writeln(' x y');

for i:= 1 to 31 do

begin

y:=a3/(a2+x*x);

writeln(x:8:4,y:8:4);

x:=x+0.1;

end;

Writeln('End program.'); Readln;

end.

5. Проведите отладку программы и проверьте полученные результаты.

6. Проверьте работу программы, где количество повторений определяется автоматически: n:=Trunc((xk-xn)/hx)+1,
где xk, xn и hx – начало, конец интервала и шаг счета.

7. Для закрепления практических приемов работы выполните упражнение 1 из раздела 3 самостоятельной работы.

2.3 Вычисления по формуле линейной интерполяции

1. Вычислить по формуле линейной интерполяции значения таблично заданной функции.

2. Таблично задана функция Y_i = f(x_i).

Вычислить по формуле линейной интерполяции

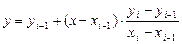
значения функции в точках x = 5.5; 7.25 .

3. В этом задании заранее не известно в каком интервале узловых точек окажется заданное значение аргумента x, а следовательно, применить оператор цикла с известным числом повторений будет затруднительно. Так как порядковый номер точки интервала интерполяции не известен, в этой задаче применим оператор цикла с неизвестным числом повторений While...do.

4. Наберите код программы, представленный на листинге 4. Самостоятельно оформите описание необходимых переменных и массивов. Организуйте ввод данных в массивы Х и Y.

Листинг 4.

. . . . .

Readln(xA);

i = 1

While xA > X[i] do i = i + 1

{Интерполяции значения yA}

yA = Y[i – 1] + (xA – X[i – 1]) *

(Y[i] – Y[i – 1]) / (X[i) – X[i – 1]);

. . . . .

5. Проведите отладку программы и проверьте полученные результаты.

2.4 Вычисление определенного интеграла

1. Вычислить интеграл в заданных границах a и b для некоторой гладкой функции f от одной переменной (с заданной точностью).

2. Алгоритм. Метод последовательных приближений, которым мы воспользуемся для решения этой задачи, состоит в многократном вычислении интеграла со все возрастающей точностью, - до тех пор, пока два последовательных результата не станут различаться менее, чем на заданное число (скажем, e = 0,001). Количество приближений нам заранее неизвестно (оно зависит от задаваемой точности), поэтому здесь применим только цикл с условием (любой из них).

3. Вычислять одно текущее значение для интеграла мы будем с помощью метода прямоугольников: разобьем отрезок [a,b] на несколько мелких частей, каждую из них дополним (или урежем - в зависимости от наклона графика функции на данном участке) до прямоугольника, а затем просуммируем получившиеся площади. Количество шагов нам известно, поэтому здесь удобнее всего воспользоваться циклом с параметром.

4. На рисунке изобразим функцию f(x) = x² (на отрезке [1,2]). Каждая из криволинейных трапеций будет урезана (сверху) до прямоугольника: высотой каждого из них послужит значение функции на левом конце участка. График станет "ступенчатым".

5. Наберите код программы, представленный на листинге 3. Самостоятельно оформите описание необходимых переменных и организуйте ввод данных - границ a и b интервала интегрирования, погрешность вычисления интеграла e. Для вычисления значений функции используйте ее предварительное описание и обращение к ней.

Листинг 3.

Function f(x:real) real;

begin f:=x*x end;

. . . . . . . . . . . . . .

step:= 1;

h:= b-a;

s_nov:= f(a)*h;

repeat

s_star:= s_nov;

s_nov:= 0;

step:= step*2;

h:= h/2;

for i:= 1 to step do

s_nov:= s_nov+f(a+(step-i)*h);

s_nov:= s_nov*h;

until abs(s_nov - s_star)<= eps;

writeln(s_nov);

6. Проведите отладку программы и проверьте полученные результаты.