Иллюстрация if и case

В качестве примера, иллюстрирующего использование операторов ветвления, приведем несколько различных реализаций функции sgn(x) - знак числа х. Из математики известно, что эта функция имеет следующие значения:

sgn(x) = -1, если x < 0;

sgn(x) = 0, если x = 0;

sgn(x) = 1, если x > 0.

Реализовать эту функцию для случая, когда х вещественное, можно следующими способами (при условии, что x:real; sgn: -1..1;):

if x=0 then sgn:= 0;

if x<0 then sgn:= -1;

if x>0 then sgn:= 1;

Это так называемая реализация "в лоб". Здесь нет никаких хитростей и никаких попыток оптимизации: даже если сработает первый вариант, второй и третий все равно будут проверены, невзирая на то, что результат уже получен.

if x=0

then sgn:= 0

else if x<0 then sgn:= -1

else sgn:= 1;

Этот вариант свободен от излишних проверок в случае, если значение переменной не положительно. Эту реализацию следует признать более эффективной, чем предыдущая :

if x=0

then sgn:=0

else sgn:=x/abs(x);

Еще одна попытка сократить текст программы. Здесь используется стандартная функция abs(), которая возвращает абсолютное значение аргумента. Проблема в данном случае состоит в том, что "/" - деление дробное, но ведь нам необходим целый, а не вещественный ответ. Для этого необходимо воспользоваться стандартной функцией округления.

if x=0

then sgn:=0

else sgn:=round(x/abs(x));

И действительно, исправленный вариант будет выдавать верный результат.

case x=0 of

true: sgn:=0;

false:

sgn:=round(x/abs(x));

end;

А вот еще один (правда, несколько неестественный) способ с использованием оператора выбора. Вся хитрость этого варианта в том, что выбирающий ветви переключатель обязан принадлежать к перечисляемому типу, именно поэтому пришлось заменить "х" на "х = 0". Напомним, что эта операция сравнения выдает результат логического типа boolean, и именно логические константы true и false фигурируют в качестве меток выбора.

Конечно же, мы перебрали далеко не все возможные способы реализации функции sgn(x). Однако уже на этом простом примере видно, что способов запрограммировать желаемое всегда больше, чем один, и вряд ли самое простое решение будет и оптимальным.

3. ПРАКТИЧЕСКАЯ РАБОТА

2.1 Программирование алгоритма ветвящейся структуры

1.Задание: Вычислить на ПЭВМ значение функции:

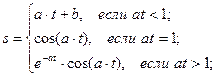
для a = 1.3, b = 1.29, t = 0.38.

2. Алгоритм решения задачи осуществляет проверку условия - at меньше, равно или больше единицы - и в зависимости от результата сравнения направляет вычисления по одной из ветвей, где осуществляется вычислительная процедура функции по заданным исходным данным. После завершения вычислений результат выводится на печать: полученное значение функции s совместно с введенными исходными данными.

3. В рабочей области редактора наберите код программы, представленный на листинге 1.

Листинг 1.

program Z1;

{$APPTYPE CONSOLE}

uses

SysUtils;

var a,b,t,s,at:real;

begin

{Ввод данных}

Write(‘Vvedite a, b, t: ’);

Readln(a,b,t);

{Вычисление результата}

at:= a*t;

if at<1 then s:= at + b

else

if at=1 then s:= cos(at)

else s:= exp(-at)*cos(at);

{Вывод на печать}

Writeln('a=', a:8:3, ' b=', b:8:3, ' t=', t:8:3);

Writeln('Result: s=', s:8:3);

Writeln('End program.'); Readln;

end.

4. В программе организован диалоговый ввод данных при помощи оператора Readln.

5. Запустите программу на решение, просмотрите и проверьте полученные результаты.

7. Сохраните проект.

8. Результаты расчета, блок-схему алгоритма и код программы поместите в отчет по лабораторной работе.

9. Для закрепления практических приемов работы выполните упражнение 1-3 из раздела 3 самостоятельной работы.

2.2 Решение геометрических задач алгебраическим способом

1. Задание: пересекаются ли две фигуры? Провести анализ взаимного расположения заданных фигур на плоскости, ответив на поставленный вопрос. Если фигуры пересекаются, то провести дальнейший анализ, ответив на такие вопросы, как:

вложенность;

внутреннее касание;

концентричность.

2. Первоначально необходимо описать состав исходных данных для определения следующих фигур на плоскости:

Круг (эллипс)

- с центром в точке (0, 0),

- с центром на оси ОХ (ОУ),

- произвольный.

Прямоугольник (квадрат) произвольный,

- со сторонами, параллельными осям координат,

- со сторонами, параллельными осям координат и центром в точке (0, 0),

- со сторонами, параллельными осям координат и центром на оси ОХ (ОУ),

- со стороной, лежащей на оси ОХ (ОУ).

Треугольник произвольный,

- равнобедренный (равносторонний) со стороной, параллельной оси ОХ (ОУ),

- равнобедренный (равносторонний) со стороной, лежащей на оси ОХ (ОУ)

Полоса произвольная,

- параллельная оси ОХ (ОУ),

- лежащая на оси ОХ (ОУ),

- с осью, лежащей на оси ОХ (ОУ).

Ромб произвольный, с осями, параллельными осям координат,

- с осями, параллельными осям координат и центром в точке (0, 0),

- с прямыми углами и осями, параллельными осям координат.

Для получения более простого решения необходимо ввести дополнительные ограничения на разворот и перемещение фигур. При любом упрощении параметры фигур не должны быть взаимозависимы.

3. Рассмотрим эту задачу на иллюстративном примере. Рассмотрим задачу «Пересекаются ли круг и эллипс?"

Для простоты решения задачи и уменьшения количества анализируемых вариантов взаимного расположения фигур введем следующее допущение: центр круга и ось эллипса лежат на оси ОХ. При таком допущении ограничивается свобода перемещения фигур, так как круг и эллипс могут передвигаться только вдоль оси ОХ.

Ограничимся также четырьмя анализируемыми ситуациями, которые представлены ниже на рисунках 1-4.

Рис.1. Фигуры не пересекаются	Рис.2. Фигуры концентрические, круг вложен в эллипс
Рис.3. Фигуры концентрические, пересекаются	Рис.4. Фигуры пересекаются

Решение задачи должно выполняться по этапам. Проиллюстрируем поэтапное выполнение.

4. Составим спецификацию задачи, заполнив следующие ее части: задача, состав входных данных, входная, выходная форма.

Спецификация:

Задача: Пересекаются ли круг и эллипс?

Ограничения: центр круга и ось эллипса лежат на оси ОХ.

Входные данные: r, x0 - радиус и центр круга (вещ.)

a, b, a0 - полуоси и центр эллипса

Входная форма: input

Выходные данные:

Выходная форма: output

5. Разработаем интерфейс задачи, поставив в качестве заглушки печать заголовка (сегмент С0).

Листинг сегмента С0.

program Z2;

{$APPTYPE CONSOLE}

uses

SysUtils;

var r, x0 : real; {радиус и центр круга}

a,b,a0: real; {полуоси и центр эллипса}

begin

Writeln(‘Kpyr и эллипс’);

Сегмент С1

Writeln('End program.'); Readln;

end.

6. Реализуем ввод данных с подсказками, вставим в сегмент С1.

Листинг сегмента С1.

{Ввод данных с подсказкой}

writeln('Ввод радиуса и центр круга');

readln (r,x0);

writeln(‘Ввод полуосей и центра эллипса');

readln(a,b,a0);

Сегмент С2

7. Составим условие пересечения фигур, записав его в раздел «Анализ фигур», в виде сегмента C2.

Применим следующий метод. Если расстояние между центрами круга и эллипса меньше, чем r+а, то фигуры пересекаются.

Вставим С2 в сегмент С1. Отладим. Для тестирования подберем значения входных данных и нарисуем рисунки для случаев:

- фигуры пересекаются,

- фигуры не пересекаются.

Листинг сегмента С2.

{Анализ фигур}

if abs(x0-a0) < r + a then

Сегмент С3

else

writeln(‘Фигуры не пересекаются’);

8. Уточним условие пересечения с точки зрения взаимного расположения фигур. Направления исследования могут быть разными, но главной целью является выявление условия вложенности фигур. Опишемнаправление исследования и раскроем случай «Пересекаются» в виде сегмента С3, где запишем следующий шаг уточнения условия пересечения. В примере проверяется концентричность фигур.

Листинг сегмента С3.

begin {Пересекаются}

Writeln(‘Фигуры пересекаются’);

If x0 = a0 then

Сегмент С4

else

writeln (‘не концентрические’)

end

Вставим С3 в сегмент С2. Отладим. Для тестирования необходимо подобрать значения входных данных и нарисовать рисунки для случаев:

- фигуры пересекаются и концентрические;

- фигуры пересекаются и не концентрические.

9. Для рассматриваемого примера, если фигуры концентрические, то условие вложенности круга в эллипс даст нам одно из решений задачи. Раскроем абстракцию концентрические в виде сегмента С4.

Применим следующий метод. Если фигуры концентрические, то круг вписан в эллипс, если его радиус меньше полуосей эллипса.

Листинг сегмента С4.

begin {концентрические}

writeln (‘концентрические’);

if (r<=a) and (r<=b) then

writeln (‘круг вложен в эллипс’)

else

writeln (‘круг не вложен в эллипс’)

end

Вставить С4 в сегмент С4 . Для тестирования подобрать значения входных данных и нарисовать рисунок для случев, когда круг вло­жен в эллипс и когда не вложен.

10. Добавим в текст программы проверку правильности входных данных и сообщение об аномалиях.

Пример. Диапазон:. r>0 и а,b>0

Аномалии: r£0 и а£0 или b£0

Листинг оболочки проверки аномалий.

Writeln(‘Kpyr и эллипс’);

{Ввод данных с подсказкой}

Writeln('Ввод радиуса и центр круга');

Readln (r,x0);

Writeln(Ввод полуосей и центра эллипса');

readln(a,b,a0);

if (r>0) and (a>0) and (b>0) then

Сегмент С2

else

Writeln('Входные данные неверные');

Необходимо подобрать тесты для проверки аномалий. Каждый тестовый набор данных должен содержать одну величину с аномальным значением при остальных допустимых данных.

11. Для закрепления практических приемов работы выполните упражнение 4 из раздела 3 самостоятельной работы.

ПРОГРАММИРОВАНИЕ АЛГОРИТМОВ
ЦИКЛИЧЕСКОЙ СТРУКТУРЫ

Операторы циклов

Для того, чтобы обработать несколько однотипных элементов, совершить несколько одинаковых действий и т.п., разумно воспользоваться оператором цикла (любым из четырех), который наилучшим образом подходит к поставленной задаче.

Оператор цикла повторяет некоторую последовательность операторов заданное число раз, которое может быть определено и динамически, т.е. уже во время работы программы.

Замечание: Алгоритмы, построенные только с использованием циклов, называются итеративными - от слова итерация, которое обозначает повторяемую последовательность действий.