Тесты для самопроверки

1. Понятие – это: а) любое слово; б) форма мышления, фиксирующая существенные признаки предмета (или класса предметов); в) языковая форма, несущая в себе какое-либо принципиально важное содержание (значение); г) группа объектов, обозначаемых одним терми­ном.

2. Объем понятия – это: а) количество букв, из которых оно состоит; б) степень значимости данного понятия; в) множество предметов, обобщаемых в понятии; г) физический объем предметов (в литрах и т.д.), мыслимых в понятии.

3. Содержание понятия – это: а) совокупность существенных признаков предме­тов, мыслимых в понятии; б) совокупность всех признаков предметов, мыслимых в понятии; в) части, на которые можно расчленить предметы, мыслимые в понятии; г) совокупность элементов его объема.

4. Что представляет собой объем понятия «учебник»: а) объем учебника; б) совокупность составляющих учебника (пере­плет, листы); в) множество всех возможных учебников; г) объем учебника в страницах.

5. Определите, что яв­ляется содержанием понятия «слон»: а) составляющие части слона: уши и хвост и т.д.; б) его душевные и интеллектуальные качества; в) рост, вес, цвет, место проживания; г) существенные признаки, по которым мы отли­чаем слона от не-слона (млекопитающее семей­ства хоботных, практически без волосяного по­крова, с бивнями и т.п.).

6. Напишите три пус­тых (нулевых) по объему понятия:

а) б) в)

7. Укажите, какие из понятий являются общими по объему: а) студент; б) Иванов; в) известный древнегреческий философ Сократ; г) известный древнегреческий философ; д) круглый квадрат; е) изучающий логику.

8. Нарисуйте схему, по­казывающую соотно­шение объемов сле­дующих понятий: А– понятие, В– абстрактное понятие, С – конкретное понятие, О – положительное понятие.

9. Укажите понятия, которые являются результатом ограни­чения понятия «ученый»: а) великий ученый; б) студент; в) Макс Борн; г) создатель квантовой механики.

10. Укажите понятия, ко­торые являются ре­зультатом обобщения понятия «минута»: а) час; б) единица времени; в) единица измерения; г) 10 минут.

11. В каких из приведен­ных ниже примеров имеет место деление объема понятия (а не деление целого на части): а) учебный год делится на два семестра; б) форма обучения может быть бюджетной или контрактной; в) понятия делятся на единичные, общие и пустые; г) в состав университета входит шесть факультетов.

12. В каких случаях деле­ние произведено правильно: а) меблировка его комнаты была весьма бедной: стол, кровать, табурет и колченогое кресло; б) преступления делятся на умышленные, неосто­рожные и должностные; в) учащиеся средних школ делятся на отличников, школьников и выпускников; г) углы в треугольнике могут быть острыми, пря­мыми и тупыми.

13. Укажите правильно построенные явные определения: а) форма – способ существования и выражения некоторого содержания; б) квадрат – равносторонний прямоугольник, у которого стороны попарно параллельны; в) домохозяйка – это не профессия; г) философ – ученый, занимающийся филосо­фией.

2. СУЖДЕНИЕ, ЕГО ВИДЫ И ЛОГИЧЕСКАЯ СТРУКТУРА

Суждение –выраженная в языковой форме (в форме высказывания) мысль, в которой что-то утверждается или отрицается.

Логические категории.Предложение включает в себя содержательные и логические части. Содержательные части – выражения языка, имеющие содержание даже в том случае, когда они взяты сами по себе. К содержательным частям относятся имена (понятия) и высказывания. Имена обозначают какие-либо объекты, высказывания описывают или оценивают ситуации или положение дел.

Логические части, или символы – выражения языка, не имеющие самостоятельного содержания, но в сочетании с одним или несколькими содержательными выражениями образующие сложные выражения. Логические символы называются также логическими постоянными.

Виды логических постоянных: 1) логические связки, позволяющие из имеющихся высказываний образовывать новые высказывания («…и…», «…или…», «есть… то…», «неверно, что…» и т.п.); 2) логические связки, позволяющие из двух понятий получить высказывание («…есть…», «все… есть…», «некоторые…есть…», «все… не есть…», «некоторые…не есть…»); 3) операторы («тот объект, который…»; 4) кванторы («все» и «некоторые»).

В качестве переменных для понятий используются буквы S, P, Q и т.д. «S есть P», «Некоторые S не есть P». Переменными для высказываний служат буквы A, B, C и т.д. «Если A, то B».

Связки, позволяющие из имен и высказываний получать новые высказываний называются пропозициональными.

Логическая символика – совокупность знаков специального, формализованного языка логики, в котором содержательные выражения заменяются буквами, а в качестве логических постоянных используются символы со строго определенными значениями. Примерами логических символов являются:

┐; ~ – знаки, служащие для обозначения отрицания; читаются «не», «неверно, что»;

; & – знаки для обозначения конъюнкции – логической связки и высказывания, содержащего такую связку в качестве главного знака; читаются: «и»;

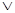– знак для обозначения неисключающей дизъюнкции – логической связки и высказывания, содержащего такую связку в качестве главного знака; читается: «или», «либо»;

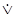– знак для обозначения строгой, или исключающей, дизъюнкции; читается: «или, или», «либо, либо»;

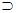→; – знаки для обозначения импликации – логической связки и высказывания, содержащего такую связку в качестве главного знака; читаются: «если, то»;

≡; ↔ – знаки для обозначения эквивалентности высказываний; читаются: «если и только если»;

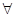– квантор общности; читается: «для всякого», «все»;

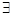– квантор существования; читается: «существует», «имеется по крайней мере один».

Простые и сложные высказывания (суждения).Высказывание – более сложное образование, чем имя. При раз­ложении высказываний на более простые части мы всегда получаем те или иные имена. Высказывание – грамматически правильное предложение, взя­тое вместе с выражаемым им смыслом (содержанием) и являюще­еся истинным или ложным. Высказывание считается истинным, если даваемое им описание соответствует реальной ситуации, и ложным, если не соответству­ет ей. «Истина» и «ложь» называются «истинностными значениями высказываний».

Высказывание (суждение) называется простым, если оно не включает дру­гих высказываний (суждений) в качестве своих частей. Высказывание (суждение) называется сложным, если оно получено с помо­щью логических связок из других более простых высказываний (суждений).