Схема логического квадрата
А – «Все S есть Р» Е – «Ни одно S не есть Р»
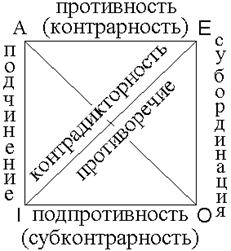
I – «Некоторые S есть Р» О – «Некоторые S не есть Р»
Отношение противности (контрарность) устанавливается между суждениями, выраженными в общей форме: А – Е. Противоположные суждения могут быть одновременно ложными, но они не могут быть одновременно истинными. Поэтому если одно из них истинно, то другое обязательно ложно. Например, из истинности суждения «Все рыбы дышат жабрами» (А) следует ложность суждения типа Е: «Ни одна рыба не дышит жабрами». В то же время общие суждения «Все знают китайский язык» и «Никто не знает китайского языка» одновременно ложны.
Отношение частичной противности, или субконтрарности, устанавливается между частными суждениями: I – О. Субконтрарные суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Поэтому если одно из них ложно, то другое обязательно истинно. Например, из ложности суждения «Некоторые явления не имеют причины» (О) следует истинность суждения типа I: «Некоторые явления имеют причину». В то же время суждения «Некоторые книги интересны» (I) и «Некоторые книги неинтересны» (О) одновременно истинны.
Логическое подчинение (субординация) характеризует отношения между общими и частными суждениями: А – I, Е – О. Для отношения подчинения характерно то, что истинность общего суждения всегда влечет истинность подчиненного ему частного суждения. Например, если истинно, что все рыбы дышат жабрами (суждение в форме А), необходимо истинным будет суждение, имеющее форму I: «Некоторые рыбы дышат жабрами». Обратно заключать от подчиненного к подчиняющему суждению можно только из ложности подчиненного. Например, из ложности суждения «Некоторые явления не имеют причины» (О) следует ложность общего суждения типа Е: «Ни одно явление не имеет причины».
Отношение противоречия (контрадикторность) устанавливается между парами суждений, несовместимыми ни по истинности, ни по ложности: А – О, Е – I. Эти пары суждений отличаются друг от друга количеством и качеством, они не могут быть ни одновременно истинными, ни одновременно ложными. Противоречащие суждения всегда отрицают друг друга. Если одно из них истинно, то другое ложно. Например, из истинности суждения «Ни один кит – не рыба» (Е) следует ложность противоречащего ему суждения «Некоторые киты – рыбы» (I).
Сложные высказывания.Простые суждения можно рассматривать как неразложимые частицы, обладающие только одним свойством: быть истинными или ложными. Простые высказывания именуются «атомарными», т.к. из них с помощью логических связок «и», «или» и т.п. строятся сложные («молекулярные») высказывания. В состав сложных суждений входит несколько субъектов или несколько предикатов.
Соединение двух суждений при помощи слова «и» дает сложное суждение, называемое конъюнкцией (  ) . Высказывания, соединяемые таким образом, называются «членами конъюнкции». Конъюнкция истинна только в случае, когда оба входящих в нее высказывания являются истинными; если хотя бы один из ее членов ложен, то и вся конъюнкция ложна.
) . Высказывания, соединяемые таким образом, называются «членами конъюнкции». Конъюнкция истинна только в случае, когда оба входящих в нее высказывания являются истинными; если хотя бы один из ее членов ложен, то и вся конъюнкция ложна.
Соединение двух суждений с помощью слова «или» дает дизъюнкцию этих суждений. Слово «или» иногда означает «одно или другое, или оба», а иногда «одно или другое, но не оба вместе». Первый смысл «или» называется соединительным или неисключающим( 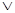 ) . Взятая в этом смысле дизъюнкция двух высказываний означает, что, они могут дополнять друг друга и быть истинными. Взятая во втором, исключающем (
) . Взятая в этом смысле дизъюнкция двух высказываний означает, что, они могут дополнять друг друга и быть истинными. Взятая во втором, исключающем ( 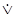 ), или строгом, смысле дизъюнкция двух суждений утверждает, что одно из высказываний истинно, а второе – ложно. Неисключающая дизъюнкция истинна, когда хотя бы одно из входящих в нее высказываний истинно, и ложна, только когда оба ее члена ложны. Исключающая дизъюнкция истинна, когда истинным является только один из ее членов, и она ложна, когда оба ее члена истинны или оба ложны.
), или строгом, смысле дизъюнкция двух суждений утверждает, что одно из высказываний истинно, а второе – ложно. Неисключающая дизъюнкция истинна, когда хотя бы одно из входящих в нее высказываний истинно, и ложна, только когда оба ее члена ложны. Исключающая дизъюнкция истинна, когда истинным является только один из ее членов, и она ложна, когда оба ее члена истинны или оба ложны.
Условное суждение (импликация) –сложное высказывание, формулируемое обычно с помощью связки «если ..., то ...» (→) и устанавливающее, что одно событие, состояние и т.п. является в том или ином смысле основанием или условием для другого. Например: «Если есть огонь, то есть дым», «Если число делится на 9, оно делится на 3» и т. п. Та часть условного высказывания, которому предпослано слово «если», называется основанием, или антецедентом (предыдущим), высказывание, после слова «то», называется следствием, или консеквентом (последующим).
Условное суждение подразумевает, что не может быть так, чтобы то, о чем говорится в его основании, имело место, а то, о чем говорится в следствии, отсутствовало. Иными словами, импликация является ложной только в том случае, когда ее основание истинно, а следствие ложно.
В терминах условного суждения обычно определяются понятия достаточного и необходимого условия: основание есть достаточное условие для следствия, а следствие – необходимое условие для основания. Типичной функцией условного высказывания является обоснование одного высказывания ссылкой на другое высказывание. Например, «Если серебро – металл, оно электропроводно».
В логике условное высказывание представляется, как правило, посредством импликативного высказывания, или импликации. Импликация истинна, когда и ее основание, и ее следствие истинны или ложны; она истинна, если ее основание ложно, а следствие истинно. Только в четвертом случае, когда основание истинно, а следствие ложно, импликация ложна.
Импликацией не предполагается, что высказывания А и В как-то связаны между собой по содержанию. В случае истинности В высказывание «если А, то B» истинно независимо от того, является А истинным или ложным и связано оно по смыслу с В или нет. Например, истинным считаются высказывания: «Если на Солнце есть жизнь, то дважды два равно четыре». Условное высказывание истинно также тогда, когда А ложно, и при этом опять-таки безразлично, истинно В или нет и связано оно по содержанию с А или нет. К истинным относятся высказывания: «Если Солнце – куб, то Земля – треугольник». В обычном рассуждении все эти высказывания вряд ли будут рассматриваться как имеющие смысл и еще в меньшей степени как истинные.
С импликацией тесно связана эквивалентность (≡), называемая иногда «двойной импликацией». Эквивалентность – сложное высказывание «А, если и только если В», образованное из высказываний А и В и разлагающееся на две импликации: «если А, то B», и «если В, то А». Например: «Треугольник является равносторонним, если и только если он является равноугольным». Термином «эквивалентность» обозначаются и связки «если и только если», «тогда и только тогда, когда» и т. п.
Если логические связки определяются в терминах истины и лжи, эквивалентность истинна тогда и только тогда, когда оба составляющих ее высказывания истинны или оба ложны. Соответственно эквивалентность является ложной, когда одно из входящих в нее высказываний истинно, а другое ложно.
Семантическая таблица
| А | В | (А  В) В)
| (А 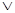 В) В)
| (А 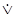 В) В)
| (А→В) | (А≡В) |
| и и л л | и л и л | и л л л | и и и л | л и и л | и л и и | и л л и |
Дата добавления: 2017-01-26; просмотров: 2128;











