Линейные электрические цепи постоянного тока
1.1.Элементы электрических цепей постоянного тока
Электромагнитные устройства с происходящими в них физическими процессами можно заменить некоторым расчетным эквивалентом – электрической цепью (ЭЦ).
Электрической цепью называют совокупность источников электрической энергии, соединенных с нагрузками. Электромагнитные процессы в ЭЦ можно описать с помощью понятий: ток – I (А), напряжение – U (В), электродвижущая сила (ЭДС) – Е (В), электрический потенциал в точке а – φa, сопротивление – R (Ом), проводимость – g (См), индуктивность – L (Гн), емкость – С (Ф).
Постоянный ток, не изменяющийся во времени ни по величине, ни по направлению, представляет собой упорядоченное «направленное» движение электрических зарядов. Носителями зарядов в металлах являются электроны, в полупроводниках – дырки и электроны, в жидкостях – ионы, в газовом разряде – электроны и ионы. Упорядоченное движение носителей зарядов в проводнике вызывается электрическим полем, создаваемым источниками электрической энергии.
Источник энергии характеризуется величиной и направлением ЭДС и величиной внутреннего сопротивления.
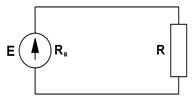
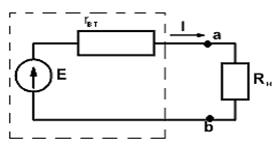
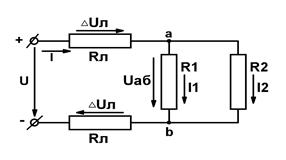
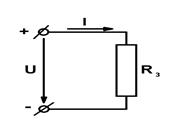
На рис. 1.1а)изображена схема неразветвленной электрической цепи.
|
|
|
Рис. 1.1.
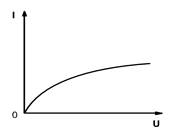
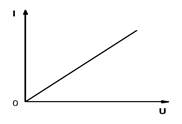
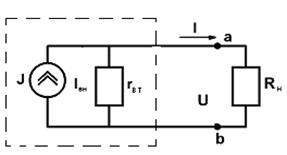
Зависимость протекающего по сопротивлению R тока от напряжения на этом сопротивлении I=f(U), называется вольтамперной характеристикой (ВАХ). Сопротивления, ВАХ которых – прямые линии (рис.1.1.б.), называются линейными, а электрические цепи с такими сопротивлениями – линейными электрическими цепями. Сопротивления, ВАХ которых не являются прямыми линиями, называют нелинейными (рис. 1.1.в.), а электрические цепи с таким сопротивлениями − нелинейными. В неразветвленной цепи через каждый участок протекает один и тот же ток. В разветвленной цепи, представленной на рис.1.2., в каждой ветви протекает свой ток.
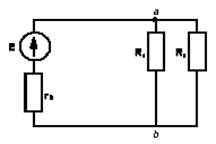
Рис. 1.2.
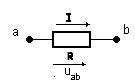
Ветвью называется участок цепи, образованный последовательно соединенными элементами, заключенными между двумя узлами а и b (рис.1.2.). Узел – это точка цепи, в которой сходится не менее трех ветвей. Если в месте пересечения двух линий нет электрического соединения, то точка не ставится.
1.2. Закон Ома для участка цепи
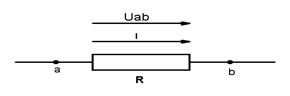
Напряжение Uab на участке a-b ЭЦ (рис.1.3.) понимают разность потенциалов между крайними точками этого участка. Ток I течет от точки «а» большего потенциала к точке «b» меньшего потенциала, т.е.  на величину падения напряжения на сопротивлении R
на величину падения напряжения на сопротивлении R
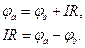
|
В соответствии с определением напряжение между точками а и b:
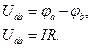
Тогда напряжение на сопротивлении R равно произведению протекающего по нему тока на величину этого сопротивления. Так определяется закон Ома для участка цепи, не содержащего ЭДС, который можно записать как
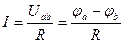
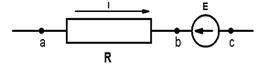
Рассмотрим участок цепи, содержащий помимо сопротивления ЭДС, Е.
|
|
|
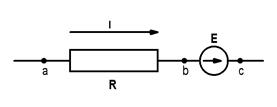
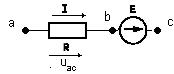
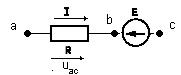
На рис. 1.4. (а и б) показаны участки цепей с источником ЭДС, по которым протекает ток I. Найдем разность потенциалов (напряжение) между точками «а» и «с». Согласно определению в обоих случаях имеем
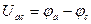 .
.
На рис.1.4.а) перемещение от точки «с» к точке «b» является встречным направлению ЭДС Е, поэтому 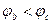 на величину Е
на величину Е
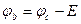 .
.
Потенциал в точке «b» на рис. 1.4.б)оказывается выше, чем в точке с на величину ЭДС Е
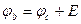 .
.
Поскольку ток течет от более высокого потенциала к более низкому, в обеих схемах а и b рис. 1.4. потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R
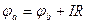 .
.
Таким образом, на рис. 1.4.а)
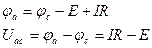 ,
,
а на рис. 1.4.б).
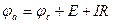 , или
, или 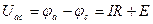 .
.
Т.о., для участка цепи, содержащего источник ЭДС, можно найти ток этого участка по разности потенциалов 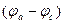 .
.
Ток для схемы рис. 1.4.а) 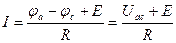 ,
,
для схемы рис.1.4.б) 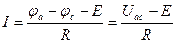 .
.
Полученные уравнения выражают закон Ома для участков цепи, включающих источники ЭДС, направленные по току и против тока.
1.3. Источник ЭДС и источник тока
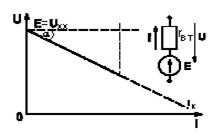
Источник энергии в схеме рис. 1.5.а), очерченный пунктирной линией, включает источник ЭДС Е и внутреннее сопротивление rвт.
Внешняя характеристика источника напряжения (или ВАХ) 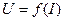 в общем случае определяется как
в общем случае определяется как 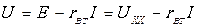 ,
,
где Uxx − напряжение при разомкнутой цепи нагрузки. Этому выражению соответствует прямая наклонная линия на рис. 1.5.а).
|
|
|
|
|
|
|
Рассмотрим два крайних случая.
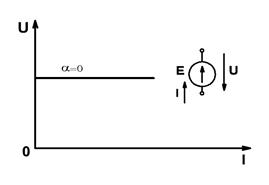
1) При 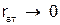 и
и 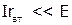 , получим
, получим 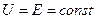 , тогда ВАХ − прямая линия, источник ЭДС (рис. 1.6.б) представляет собой идеализированный источник питания, напряжение на зажимах которого не зависит от величины тока.
, тогда ВАХ − прямая линия, источник ЭДС (рис. 1.6.б) представляет собой идеализированный источник питания, напряжение на зажимах которого не зависит от величины тока.
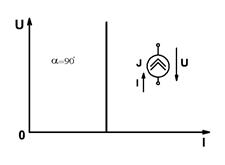
2) Если у источника питания повышается ЭДС и внутреннее сопротивление 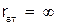 ,
, 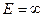 , то
, то 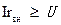 , тогда
, тогда 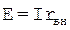 . Ток источника тока
. Ток источника тока 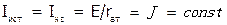 , и ВАХ примет вид, показанный на рис.1.6.в).
, и ВАХ примет вид, показанный на рис.1.6.в).
Следовательно, источник тока представляет собой идеализированный источник питания, в котором ток не зависит от сопротивления нагрузки.
При построении эквивалентных схем замещения ветви, содержащие источники напряжения, замыкают накоротко (rвт=0), а ветви с источниками тока ликвидируют (т. к. 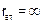 ). Ток в нагрузке
). Ток в нагрузке 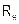 для схем рис. 1.6.б)и в) одинаков;
для схем рис. 1.6.б)и в) одинаков;
для источника ЭДС 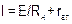 , для источника тока
, для источника тока 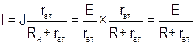 .
.
Осуществим переход от схемы с источником тока к схеме с источником ЭДС. Пусть в схеме б) 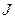 =50 А,
=50 А, 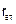 =2 Ом, в схеме а) ЭДС
=2 Ом, в схеме а) ЭДС 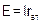 =100 В. Следовательно, параметры эквивалентной схемы рис.1.5.а) равны
=100 В. Следовательно, параметры эквивалентной схемы рис.1.5.а) равны 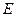 = 100 В,
= 100 В, 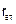 = 2 Ом.
= 2 Ом.
Можно пользоваться любым эквивалентом, но в основном пользуются источником напряжения.
1.4. Методы расчета электрических цепей постоянного тока
1.4.1.Расчет по законам Кирхгофа
Все ЭЦ подчиняются первому и второму законам Кирхгофа.
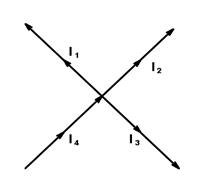 Первый закон Кирхгофа можно сформулировать двояко. Алгебраическая сумма токов, приходящих к любому узлу схемы, равна нулю. Сумма токов, приходящих к узлу, равна сумме токов, уходящих от узла.
Первый закон Кирхгофа можно сформулировать двояко. Алгебраическая сумма токов, приходящих к любому узлу схемы, равна нулю. Сумма токов, приходящих к узлу, равна сумме токов, уходящих от узла.
| |
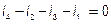 ;
; 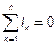 ,
,
где n – число ветвей, образующих узел.
|
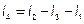 .
.
Физически 1-й закон Кирхгофа означает, что при движении электронов по цепи ни в одном из узлов заряды не накапливаются.
Второй закон Кирхгофа так же можно сформулировать двояко. Алгебраическая сумма падений напряжений на резистивных элементах в любом замкнутом контуре равно алгебраической сумме ЭДС. 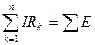 .
.
В каждую из сумм составляющие слагаемые входят со знаком «+», если они совпадают с направлением обхода контура, и со знаком «-», если не совпадают.
Алгебраическая сумма напряжений участков вдоль любого замкнутого контура равна нулю 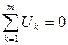 ,
,
где m – число участков контура, так, для периферийного контура схемы рис.1.8. имеем 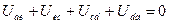 .
.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменений токов и напряжений во времени.
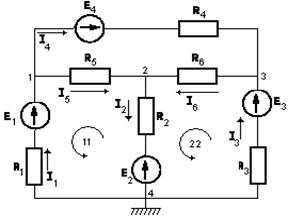
При составлении уравнений для расчетов токов в ветвях схемы с помощью законов Кирхгофа учитываем, что в каждой ветви течет свой ток.
|
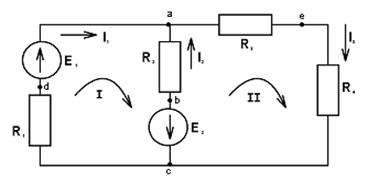
Обозначим число всех ветвей схемы через «б», число ветвей, содержащих источники тока, через «бист.т», и число узлов – через «у». Так как токи в ветвях с источниками тока неизвестны, то число неизвестных токов запишем как «б» - «бист.т».
Перед тем как составить уравнения, необходимо а) произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме; б) выбрать положительные направления контуров для составления уравнений по 2-ому закону Кирхгофа.
Желательно во всех контурах положительные направления обхода выбирать одинаковыми, например, по часовой стрелке, как показано на рис. 1.9.
Чтобы получить независимые уравнения, по 1-ому закону Кирхгофа составляют число уравнений, равное числу узлов без единицы, т.е. «у-1». По 2-ому закону Кирхгофа составляют число уравнений, равное числу ветвей без источников тока б - бист.т, за вычетом числа уравнений, составленных по 1- му закону Кирхгофа. В рассмотренном (б - бист.т)-(у -1) = 3 – 2 + 1 = 2.
При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в контуры, для которых уже записаны уравнения. Такие контуры условно можно назвать независимыми.
По 1- ому закону Кирхгофа составляем одно уравнение 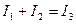 .
.
По 2-ому закону Кирхгофа надо составить два уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.
Для контура 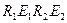
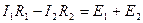 , знак «+» взят перед
, знак «+» взят перед 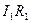 , потому что направление тока
, потому что направление тока 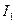 совпадает с направлением обхода контура; знак «-» перед
совпадает с направлением обхода контура; знак «-» перед 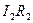 показывает, что направление
показывает, что направление 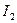 встречно обходу контура.
встречно обходу контура.
Для контура 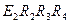
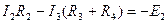 .
.
Используя законы Кирхгофа, можно для любой разветвленной электрической цепи составить необходимое число уравнений, путем совместного решения которых можно найти все определяемые величины (например, токи), а также установить зависимости между ними.
1.4.2. Преобразование ЭЦ с различным соединением сопротивлений
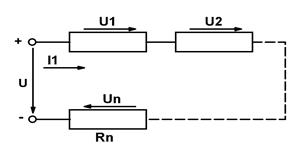
1. Последовательным соединением сопротивлений называется такое, когда конец первого сопротивления соединяется с началом второго, конец второго сопротивления с началом третьего и т.д. Начало первого сопротивления и конец последнего подключаются к источнику питания или к каким-либо точкам ЭЦ (рис. 1. 9.). Во всех сопротивлениях протекает один и
|
|
Ток в цепи, напряжения на сопротивлениях и потребляемые ими мощности определяются следующими соотношениями.
1. Эквивалентное сопротивление электрической цепи 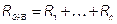 .
.
2. Ток в сопротивлениях цепи 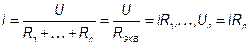 .
.
3. Напряжение и мощность, подводимые к электрической цепи с последовательным соединением сопротивлений равны, соответственно, сумме напряжений и мощностей 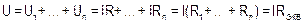 ,
,
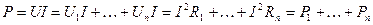 .
.
4. Напряжение и мощности распределяются пропорционально сопротивлениям 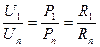 .
.
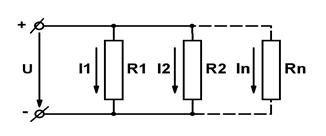
2. При параллельном соединении сопротивлений соединяются между собой как начало всех сопротивлений, так и их концы (рис. 1.10.).
Характерным для параллельного соединения является одно и то же напряжение на зажимах всех сопротивлений. Параллельно соединяются обычно различные приемники электрической энергии, рассчитанные на одно и то же напряжение. При параллельном соединении не требуется согласовывать номинальные данные приемников, возможно включение и отключение любых приемников независимо от остальных, а при выходе из строя любого из них остальные остаются включенными.
|
|
|
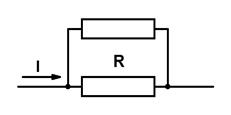
Параллельное соединение можно применить, если требуется уменьшить сопротивления какого-либо участка электрической цепи, как показано на рис. 1.10.б).
Токи и мощности параллельно соединенных ветвей рис.1.10.а) при 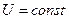 не зависят друг от друга.
не зависят друг от друга.
1. Общий ток равен сумме токов параллельно соединенных ветвей
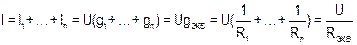 ,
,
где: 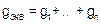 − эквивалентная проводимость, равная
− эквивалентная проводимость, равная 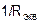
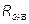 − эквивалентное сопротивление,
− эквивалентное сопротивление, 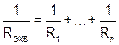 .
.
2. Токи и мощности в ветвях в ветвях вычисляются по формулам 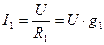 ;
; 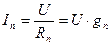 ;
; 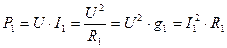 ;
; 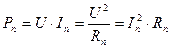 .
.
3. Отношение токов и мощностей равно отношению проводимостей и обратно пропорционально отношению сопротивлений
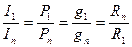 .
.
При увеличении параллельно соединенных сопротивлений эквивалентная проводимость ЭЦ увеличивается, а эквивалентное сопротивление уменьшается, что приводит к увеличению тока. Если напряжение остается const, то увеличивается также общая мощность.
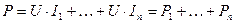 , или
, или 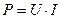 .
.
3. Смешанным или последовательно-параллельным называется такое соединение сопротивлений, при котором на одних участках ЭЦ сопротивления соединены параллельно, а на других последовательно.
Анализ и расчет ЭЦ со смешанным соединением сопротивлений производится методом преобразований. Электрическая цепь (рис. 1.11.а) заменяется последовательно эквивалентными цепями до образования схемы, изображенной на рис. 1.11.б).
|
|
|
В соединении «треугольником» конец одного из сопротивлений соединяется с началом следующего и т.д., а узлы a,b,c подключаются к остальной части ЭЦ. В соединении «звездой» все концы соединяются вместе, а начала фаз подключаются к схеме. Если заменить сопротивление 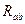 ,
, 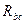 ,
, 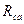 , соединенные в треугольник, эквивалентными сопротивлениями, соединенными звездой, то получим цепи со смешанным соединением сопротивлений.
, соединенные в треугольник, эквивалентными сопротивлениями, соединенными звездой, то получим цепи со смешанным соединением сопротивлений.
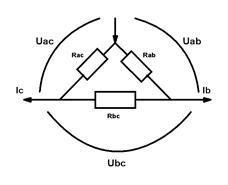
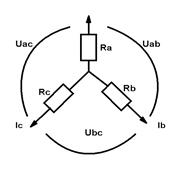
Преобразование «звезды» в «треугольник»
|
|
|
После замены токи 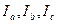 и направления
и направления 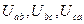 должны остаться без изменений.
должны остаться без изменений.
Для «треугольника» 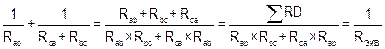 ;
;
Для соединения звездой 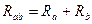
По условию эквивалентности эквивалентные сопротивление обеих схем равны 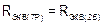 , следовательно, можно записать
, следовательно, можно записать
1) 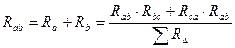 ;
;
Структуры соединением «треугольник» и «звезда» по отношению к узлам симметричны, поэтому циклично запишем
2) 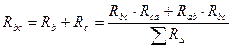 ;
;
3) 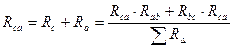 .
.
Сложим 1) и 3), вычтем 2), всё поделим на 2, получим
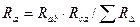 ,
, 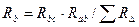 ,
, 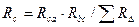 .
.
Если 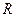 в «треугольнике» равны, то и в «звезде» равны:
в «треугольнике» равны, то и в «звезде» равны: 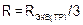 .
.
Возможно обратное преобразование звезды из резистивных элементов в эквивалентный треугольник. Для этого надо попарно перемножить 1) и 3) и сложить, затем вынести общий множитель и полученное уравнение разделить на 3)уравнение, т.е. 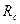 . Далее поочередно поделить то же уравнение на
. Далее поочередно поделить то же уравнение на 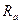 и
и 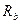 .
.
Путем циклической подстановки индексов при преобразовании звезды в треугольник получим 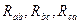
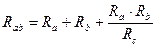 ,
, 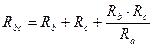 ,
, 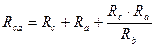 .
.
На рис. 1.13. поясняется упрощение схемы путем последовательной замены эквивалентными цепями при преобразовании «треугольника» в «звезду».
| |
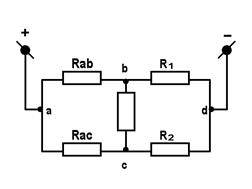 б)
б) 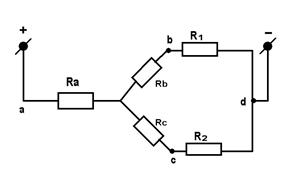
|
| |
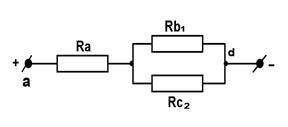 г)
г) 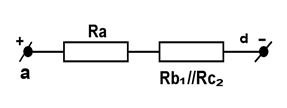
1.4.3. Метод контурных токов
При расчете методом контурных токов за искомое принимают контурные токи. Число неизвестных равно числу уравнений, которые необходимо было составить по II закону Кирхгофа. Следовательно, в методе контурных токов меньшее число уравнений, чем в методе на основе законов Кирхгофа.
|
|
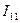 , в правом – контурный ток
, в правом – контурный ток 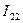 . Для каждого из контуров составим уравнение по II закону Кирхгофа.
. Для каждого из контуров составим уравнение по II закону Кирхгофа.
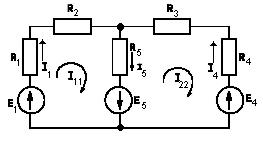
Рис. 1.14.
Для первого контура 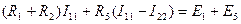 , или
, или
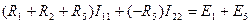 .
.
Для второго контура 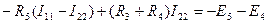 , или
, или
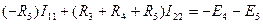 .
.
В уравнении для 1-го контура множитель при токе 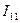 , являющийся суммой сопротивлений первого контура, обозначим через
, являющийся суммой сопротивлений первого контура, обозначим через 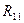 . Множитель при токе
. Множитель при токе 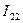 , взятый со знаком «-», обозначим через
, взятый со знаком «-», обозначим через 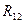 . Уравнения для 1-го и 2-го контуров примут вид
. Уравнения для 1-го и 2-го контуров примут вид 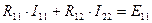 ,
, 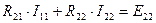 , здесь
, здесь
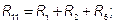
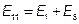 ;
; 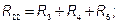
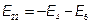 ;
; 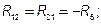
где 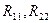 − полное или собственное сопротивление первого и второго контуров, соответственно.
− полное или собственное сопротивление первого и второго контуров, соответственно.
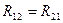 − взаимное сопротивление смежной ветви между первым и вторым контурами, взятые со знаком «-».
− взаимное сопротивление смежной ветви между первым и вторым контурами, взятые со знаком «-».
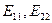 − контурные ЭДС первого и второго контуров, равные алгебраической сумме ЭДС, входящих в эти контуры.
− контурные ЭДС первого и второго контуров, равные алгебраической сумме ЭДС, входящих в эти контуры.
Со знаком «+» входят ЭДС, направление которых совпадает с направлением обхода контура.
Отметим, что члены, содержащие полные контурные сопротивления, положительны, а взаимные – отрицательны.
Если в схеме будет три контура, то система уравнений примет вид
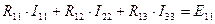 ;
;
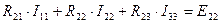 ;
;
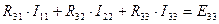 ;
;
Или в матричной форме
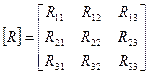 ,
, 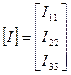 ,
, 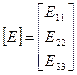 .
.
Если в электрической цепи имеется «n» независимых контуров, то количество уравнений тоже равно n. Решение удобно проверить методами Крамера и Гаусса.
Общее решение системы n уравнений относительного тока 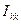
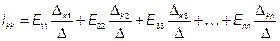 ,
,
где 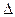 и
и 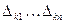 − определители системы.
− определители системы.
По найденным токам ищем действительные токи 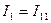 ;
; 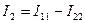 ;
; 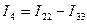 ;
; 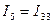 ;
; 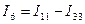 ,
, 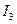 находим из 1-го закона Кирхгофа.
находим из 1-го закона Кирхгофа.
1.4.4. Метод узловых потенциалов.
а)
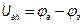
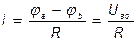
 б)
б)
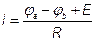 б
б
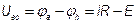
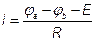 в)
в)
Рис.1.15
|
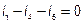 ,
, 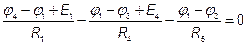 ;
;
или через проводимости
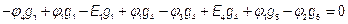 ,
,
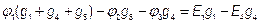 ,
,
для 2-го узла
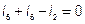 ,
, 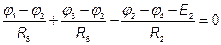 ,
,
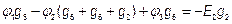 ,
,
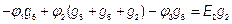 ,
,
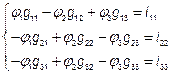
1) Узловая проводимость узла − это сумма проводимости ветвей, сходящихся в данном узле.
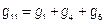 ;
; 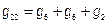 ;
; 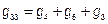 .
.
2) Взаимная проводимость двух любых узлов − сумма проводимости ветвей, включённых между этими узлами.
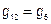 ;
; 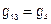 ;
; 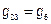 ;
; 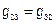 ;
; 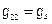 .
.
3) Узловой ток − сумма произведений ЭДС на проводимости ( 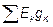 ) ветвей, сходящихся в данном узле. Если ЭДС направлена к узлу, то берем ее как «+»; от узла «−».
) ветвей, сходящихся в данном узле. Если ЭДС направлена к узлу, то берем ее как «+»; от узла «−».
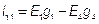 ;
; 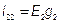 ;
; 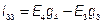 .
.
4) В системе уравнений все члены, содержащие узловые проводимости берутся со знаком «+», а содержащие взаимные проводимости − со знаком «-».
Решив систему уравнений, найдем потенциалы всех узлов. По этим потенциалам определяем токи ветви 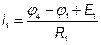 ,
,
если ток получился со знаком «-», значит в действительности он направлен в противоположную сторону.
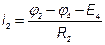 ;
; 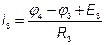 ;
; 
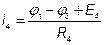 ;
; 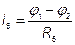 ;
; 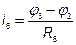 .
.
1.4.5. Метод узлового напряжения (2-х узлов)
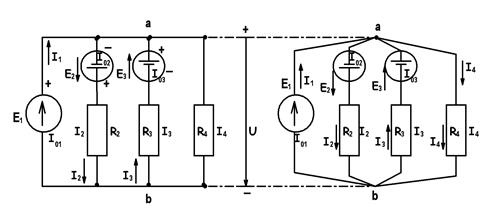
Метод узлового напряжения − это частный случай метода узловых потенциалов, дает возможность упрощенного расчета ЭЦ, содержащей несколько параллельно соединенных ветвей (рис. 1.16.а).
Поскольку в верхних и нижних шинах схемы не включено каких-либо сопротивлений, то электрическую цепь рис.1.16.а) можно заменить цепью, изображенной на рис. 1.16.б).
В зависимости от величин и направлений ЭДС между узловыми точками а) и б) установится определенное узловое напряжение U. Если оно известно, то легко найти токи между двумя узлами а и б.
Выберем условные положительные направления токов, как показано на рис. 1.16. По 2-ому закону Кирхгофа для контура, включающего 1-ю ветвь
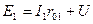 ,
, 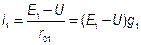 .
.
Так же найдем токи ветвей 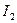 и
и 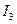
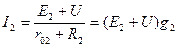 ,
, 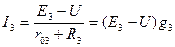 .
.
По закону Ома найдем ток для 4-ой ветви 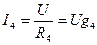 .
.
|
|
|
Для вывода формулы, позволяющей определить напряжение U, запишем уравнение по 1- му закону Кирхгофа для узла а
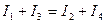 .
.
Заменим токи полученными выражениями

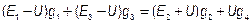 .
.
После группировки членов получим формулу узлового напряжения
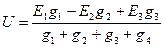 , или в общем виде
, или в общем виде  .
.
1.4.6. Метод наложения токов
|
Принцип наложения заключается в следующем: при воздействии 2-х источников ток каждой ветви определяется как сумма токов  от действия каждого из источников (рис. 1.17.а). При определении токов в каждой ветви
от действия каждого из источников (рис. 1.17.а). При определении токов в каждой ветви
|
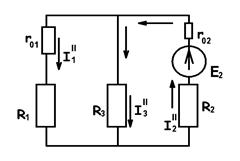
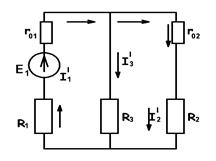
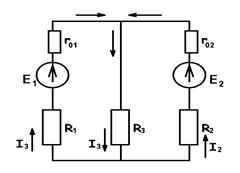 а) б) в)
а) б) в)
Рис. 1.17.
|
|
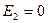 . Оставляем
. Оставляем 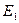
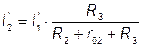
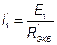
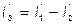
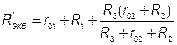
Это приведенные токи.
|
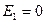 . Оставляем
. Оставляем 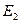 , остальных нет.
, остальных нет.
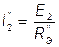
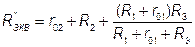
|
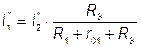 ;
; 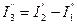 .
.
Это приведенные токи.
Чтобы найти действительные токи произведем наложение. Найдем алгебраическую сумму токов в ветвях.
Если составляющие токов в ветви направлены в одну сторону, то действительный ток ветви равен их сумме; если встречно – то действительный ток равен их разности 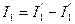 ;
; 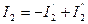 ;
; 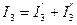 .
.
1.4.7. Метод эквивалентного генератора
Удобен, если необходимо найти ток в одной ветви сложной ЭЦ, не рассчитывая токи в других ветвях. Принцип метода состоит в замене сложной ЭЦ активным 2-х полюсником А – эквивалентным источником энергии.
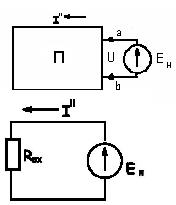 Действуем методом наложения, цепь разбиваем на 2 части по сечению ab (рис.1.18.а.).
Действуем методом наложения, цепь разбиваем на 2 части по сечению ab (рис.1.18.а.).
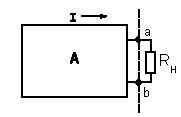
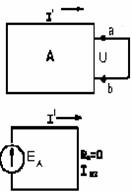
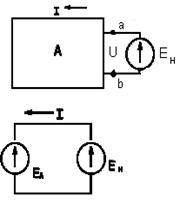
а) б) в) г)
Рис.1.18.
Имеем:
|
|
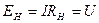
|
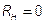
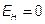
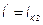 .
.
|
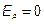 , то есть все ЭДС в активном 2-х полюснике равны 0, то активный 2-х полюсник А не действует и становится пассивным 2-х полюсником П с Rвх. Действует только ЕН=U. Ток пассивного 2-х полюсника
, то есть все ЭДС в активном 2-х полюснике равны 0, то активный 2-х полюсник А не действует и становится пассивным 2-х полюсником П с Rвх. Действует только ЕН=U. Ток пассивного 2-х полюсника
|
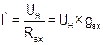 .
.
Проведем наложение 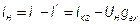 ,
, 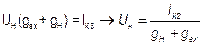 .
.
Если 2-х полюсник работает в режиме холостого хода, когда 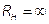 ,
, 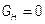
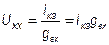 ;
; 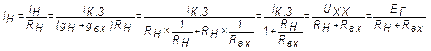 .
.
Т.о., активный 2-х полюсник А можно заменить эквивалентным источником напряжения, ЭДС которого равна Uхх активного 2-х полюсника (Ег=Uхх), а внутреннее сопротивление равно входному сопротивлению активного 2-х полюсника Rвт = Rвх..
|
1.5. Энергетический баланс в электрических цепях
При протекании токов по сопротивлениям в них выделяется тепло. На основании закона сохранения энергии количество тепла, выделяемого в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источниками питания.
В случаях, когда направление тока I, протекающего через источник ЭДС Е, совпадает с направлением ЭДС, то источник ЭДС поставляет в цепь в единицу времени энергию, и произведение EI входит в уравнение энергетического баланса с положительным знаком.
Если направление тока I встречно направлению ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккомулятор) и произведение EI входит в уравнение энергетического баланса с отрицательным знаком.
Уравнение энергетического баланса при питании ото всех источников ЭДС имеет вид 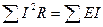
Общий вид уравнения энергетического баланса с учетом энергии, доставляемой источниками тока, выражается как 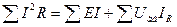 .
.
Дата добавления: 2017-01-26; просмотров: 7296;












