Граничные условия для электрического поля на границе раздела диэлектрик – диэлектрик.
Выделим небольшой участок раздела двух диэлектриков, который в пределе может считаться плоским. В электрическом поле в каждом из диэлектриков в близи поверхности раздела появятся поляризационные заряды.
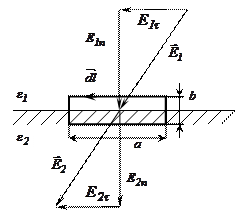
| Обозначим напряженность поля в диэлектриках через 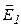 и и 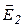 , затем разложим их на составляющие: нормальную и тангенциальную (рис. 18.6). Выберем небольшой прямоугольный контур длиной , затем разложим их на составляющие: нормальную и тангенциальную (рис. 18.6). Выберем небольшой прямоугольный контур длиной 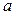 и шириной и шириной 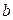 , который проходит через оба диэлектрика. Граничные условия для тангенциальных составляющих определяются из требования равенства нулю циркуляции , который проходит через оба диэлектрика. Граничные условия для тангенциальных составляющих определяются из требования равенства нулю циркуляции 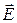 по выбранному контуру по выбранному контуру 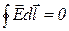 . Интегрируя по контуру и устремляю . Интегрируя по контуру и устремляю 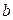 к нулю ( к нулю ( 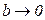 ), получим ), получим 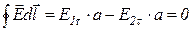
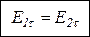
|
| Рис. 18.6 |
Тангенциальная составляющая вектора напряженности электрического поля является одинаковой по обе стороны границы раздела (не претерпевает скачка).
С помощью соотношения 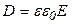 получим:
получим:
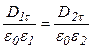 ,
,
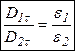
Тангенциальная составляющая вектора электрического смещения на границе раздела диэлектриков испытывает скачок и изменяется прямо пропорционально диэлектрической проницаемости среды.
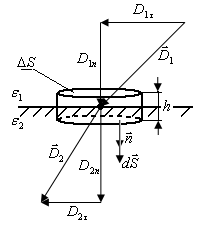
Теперь возьмем на границе диэлектриков воображаемую цилиндрическую поверхность высотой 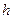 с основанием с основанием 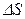 (рис.18.7). Применим теорему Гаусса (для диэлектриков). (рис.18.7). Применим теорему Гаусса (для диэлектриков).
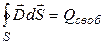 Поток вектора
Поток вектора 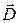 через поверхность цилиндра с учетом направления внешних нормалей равен, при устремлении высоты к нулю ( через поверхность цилиндра с учетом направления внешних нормалей равен, при устремлении высоты к нулю ( 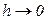 ). ).
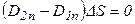 (т.к. свободных зарядов на границе раздела диэлектрика нет). (т.к. свободных зарядов на границе раздела диэлектрика нет).
| 
|
| Рис. 18.7 |
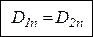
Нормальные составляющие вектора электрического смещения является одинаковыми по разные стороны границы раздела, не испытывая скачок.
Используя связь между 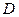 и
и 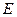
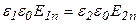 ,
,
получим
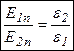
Нормальные составляющие вектора напряженности поля на границе раздела двух диэлектриков испытывают скачок и изменяются обратно пропорционально диэлектрической проницаемости среды.
Дата добавления: 2017-01-26; просмотров: 2436;











