Теорема Гаусса для электрического поля в диэлектрике. Электрическое смещение.
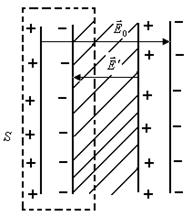
| Пусть имеются две бесконечно длинные разноименно заряженные плоскости плоского конденсатора с полем 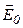 . В пространстве между ними внесем пластину из диэлектрика (рис. 18.3). В результате образования связанных поляризованных зарядов на поверхности диэлектрика, находящегося в электрическом поле, возникает дополнительное электрическое поле поляризационных зарядов диэлектрика . В пространстве между ними внесем пластину из диэлектрика (рис. 18.3). В результате образования связанных поляризованных зарядов на поверхности диэлектрика, находящегося в электрическом поле, возникает дополнительное электрическое поле поляризационных зарядов диэлектрика 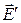 . По принципу суперпозиции электрическое поле в диэлектрике равно . По принципу суперпозиции электрическое поле в диэлектрике равно 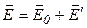 . Выделим гауссову поверхность . Выделим гауссову поверхность 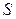 , охватывающую положительно заряженную пластину конденсатора и проходящую через диэлектрик (рис. 18.3). , охватывающую положительно заряженную пластину конденсатора и проходящую через диэлектрик (рис. 18.3).
|
| Рис. 18.3 |
Запишем теорему Гаусса. При суммировании зарядов учтем свободные заряды конденсатора и связанные не скомпенсированные заряды диполей диэлектрической среды (на поверхности диэлектрика).
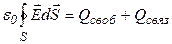 (*)
(*)
Обозначим поверхностную плотность связанных зарядов 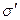 . Их результирующий заряд
. Их результирующий заряд 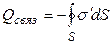 («минус» учитывает знак связанных зарядов).
(«минус» учитывает знак связанных зарядов).
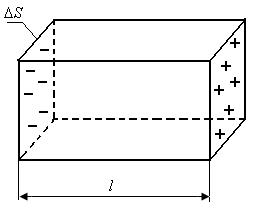
Свяжем вектор поляризованности с плотностью связанных зарядов. Выделим из диэлектрика прямоугольный параллелепипед с гранями, параллельными внешнему полю 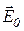 , длиной , длиной 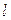 и основанием и основанием 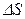 (рис. 18.4). Поверхностный заряд на основании параллелепипеда (рис. 18.4). Поверхностный заряд на основании параллелепипеда 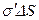 . Дипольный момент параллелепипеда обозначим . Дипольный момент параллелепипеда обозначим 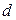 (чтобы не перепутать с (чтобы не перепутать с 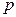 - элементарным дипольным моментом): - элементарным дипольным моментом):
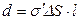
| 
|
| Рис. 18.4 |
С другой стороны из определения поляризованности дипольный момент параллелепипеда можно выразить как 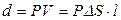 . Приравнивая правые части
. Приравнивая правые части 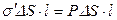 , получим
, получим 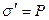 . Как показывает соответствующий расчет, в общем случае произвольного расположения параллелепипеда в пространстве между пластинами конденсатора, плотность поляризационного заряда в произвольной точке поверхности равна нормальной составляющей (перпендикулярной к поверхности
. Как показывает соответствующий расчет, в общем случае произвольного расположения параллелепипеда в пространстве между пластинами конденсатора, плотность поляризационного заряда в произвольной точке поверхности равна нормальной составляющей (перпендикулярной к поверхности 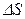 ) поляризованности в этой точке поверхности
) поляризованности в этой точке поверхности 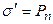 , тогда
, тогда 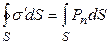 . Поскольку нормальная составляющая
. Поскольку нормальная составляющая 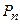 равна скалярному произведению
равна скалярному произведению 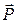 на единичный вектор нормали
на единичный вектор нормали 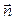 т. е.
т. е. 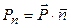 , то
, то 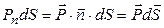 , тогда
, тогда 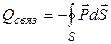 .
.
Подставляя последнее выражение в (*), получим 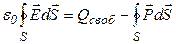 , или
, или 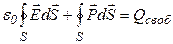 . Тогда
. Тогда 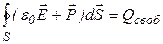 .
.
Обозначим
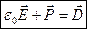 (**)
(**)
Вектор 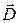 называется вектором электрического смещения (или электрическим смещением). В результате получим:
называется вектором электрического смещения (или электрическим смещением). В результате получим:
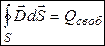
Теорема Гаусса для поля в диэлектрике: поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов.
Дата добавления: 2017-01-26; просмотров: 2266;











