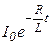Токи размыкания и замыкания.
а) Токи размыкания (экстраток размыкания) можно наблюдать с помощью следующей схемы (рис. 25.8). Если разомкнуть ключ К, то магнитный поток в катушке 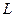 будет исчезать и в ней возникнет экстраток самоиндукции
будет исчезать и в ней возникнет экстраток самоиндукции 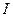 (экстраток размыкания). В соответствии с правилом Ленца он будет препятствовать убыванию магнитного потока, и направлен в катушке так же, как убывающий ток.
(экстраток размыкания). В соответствии с правилом Ленца он будет препятствовать убыванию магнитного потока, и направлен в катушке так же, как убывающий ток.
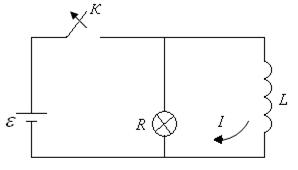
| Сила тока в контуре 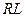 в соответствии со вторым законом Кирхгофа будет удовлетворять уравнению: в соответствии со вторым законом Кирхгофа будет удовлетворять уравнению:
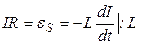 Разделив обе части на
Разделив обе части на 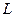 и перенеся правую часть уравнения в левую, получим: и перенеся правую часть уравнения в левую, получим:
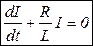
|
| Рис. 25.8 |
Это линейное дифференциальное уравнение. Составим характеристическое уравнение: 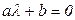 , где
, где 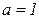 ,
, 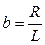 . Корень характеристического уравнения
. Корень характеристического уравнения 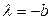 .
.
| Решение дифференциального уравнения: 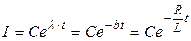 .
При .
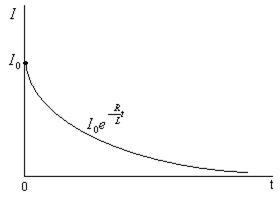
При 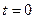 начальное значение тока начальное значение тока 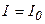 . Следовательно, подставив . Следовательно, подставив 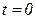 получим значение константы получим значение константы 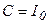 . Тогда решение дифференциального уравнения будет иметь вид: . Тогда решение дифференциального уравнения будет иметь вид:
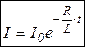
| ||
| Рис. 25.9 |
Ток убывает экспоненциально (рис. 25.9). Скорость убывания тока определяется величиной 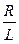 , имеющей размерность времени. Обозначим
, имеющей размерность времени. Обозначим 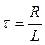 . При
. При 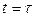 сила тока уменьшается в
сила тока уменьшается в 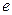 раз. Индуктивность как бы задерживает убывание тока.
раз. Индуктивность как бы задерживает убывание тока.
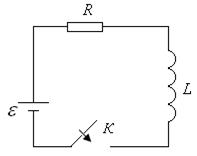
| б) Ток замыкания. Рассмотрим схему на рис. 25.10. По 2-му закону Кирхгофа:
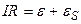 , ,
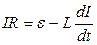 .
Разделим обе части на .
Разделим обе части на 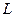 и перенесем и перенесем 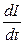 в левую часть: в левую часть:
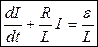 (**) (**)
|
| Рис. 25.10 |
Это линейное неоднородное дифференциальное уравнение. Общее решение линейного неоднородного уравнения можно получить, прибавив любое его частное решение к общему решению соответствующего однородного уравнения.
Общее решение однородного уравнения:
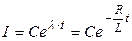
Частное решение может быть, например, 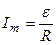 . (Убедимся в этом, подставим это решение в уравнение (**):
. (Убедимся в этом, подставим это решение в уравнение (**): 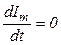 ;
; 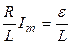 ;
; 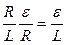 ;
; 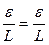 ).
).
| Общее решение неоднородного уравнения будет иметь вид: 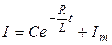 Найдем константу
Найдем константу 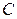 . При . При 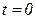 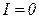 , тогда , тогда 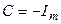 , отсюда общее решение неоднородного уравнения для токов замыкания: , отсюда общее решение неоднородного уравнения для токов замыкания:
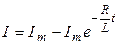 , ,
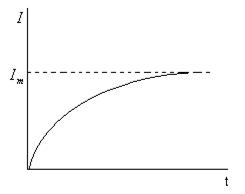
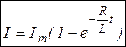 (рис. 25.11).
(рис. 25.11).
|
| Рис. 25.11 |
В случае тока замыкания индуктивность задерживает нарастание тока.
4. Энергия магнитного поля.
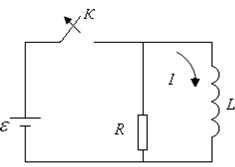
Рассмотрим схему на рис. 25.12. При замкнутом ключе в соленоиде установится ток 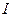 , который обусловит магнитное поле, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление , который обусловит магнитное поле, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление 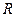 будет течь постепенно убывающий ток, поддерживаемый возникающей в соленоиде ЭДС самоиндукции. Работа, совершаемая этим током за счет энергии магнитного поля за время будет течь постепенно убывающий ток, поддерживаемый возникающей в соленоиде ЭДС самоиндукции. Работа, совершаемая этим током за счет энергии магнитного поля за время 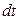 : :
| 
|
| Рис. 25.12 |
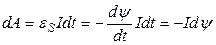 ,
,
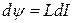 , тогда
, тогда
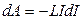 .
.
Ток совершает работу изменяя свое значение от 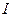 до 0:
до 0:
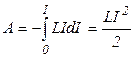 .
.
Подставляя значение индуктивности соленоида 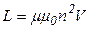 и учитывая, что
и учитывая, что 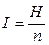 :
:
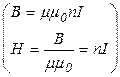 .
.
Учитывая все, получим: 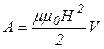 . Поскольку работа совершается за счет энергии магнитного поля катушки, то
. Поскольку работа совершается за счет энергии магнитного поля катушки, то 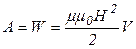 , отсюда объемная плотность энергии магнитного поля:
, отсюда объемная плотность энергии магнитного поля:
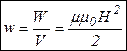
Вопросы для самоконтроля.
1. Что такое магнитный поток? Как он определяется?
2. Что выражает закон электромагнитной индукции Фарадея и какова его формула?
3. Что выражает правило Ленца?
4. Положительные и отрицательный проявления токов Фуко.
5. Какое явление называется самоиндукцией? Взаимоиндукцией?
6. Что такое индуктивность контура?
7. Какую роль играет индуктивность для токов размыкания и замыкания?
8. Найдите выражение для магнитной энергии тока и объемной плотности энергии магнитного поля.
Лекция № 26
Дата добавления: 2017-01-26; просмотров: 2024;