Вынужденные колебания системы с произвольным числом степеней свободы.

Для наглядности возьмем также балку с расположенными на ней массами 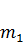, , 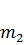… 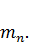На систему действуют вибрационные нагрузки P(t), M(t) и т.д.(рис. 36).

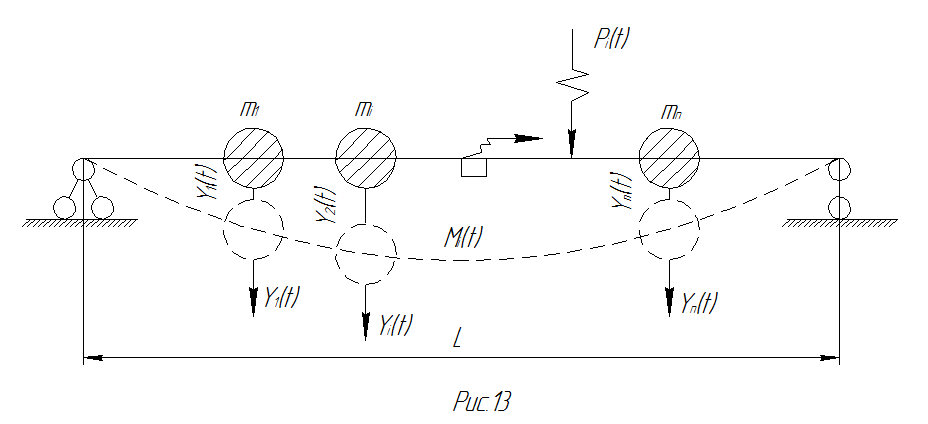
Рис. 36 Расчетная схема балки, балку с расположенными на ней массами точечными массами

Ограничимся рассмотрением случая, когда все нагрузки изменяются по гармоническому закону: ;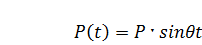

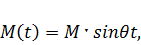где круговая частота 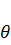для всех нагрузок одинакова.

В этом случае через некоторый промежуток времени нагрузка полностью подчинит себе систему, и она начнет совершать установившиеся колебания по закону

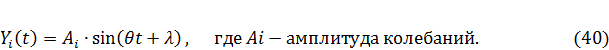
Этот закон показывает, что частота вынужденных колебаний системы совпадает с частотой пульсаций вибрационной нагрузки .

В том случае, если частота собственных колебаний системы совпадает с частотой пульсаций вибрационной нагрузки 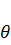, то наступает резонанс, явление крайне нежелательное в инженерной практике. При резонансе возникают большие деформации системы и значительные инерционные силы, часто опасные для сооружений даже при малой возмущающей нагрузке.

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с некоторой другой частотой, определяемой из параметров колебательной системы, таких как внутренняя (собственная) частота, коэффициент вязкости и т. п. В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.

Определим максимальные инерционные силы.

Рассмотрим случай, когда «объемная» масса совершает как линейные, так и вращательное движения в плоскости. Движение в плоскости «объемной» массы можно разложить на два вида движения:

1) поступательное движение пo направлению оси Y (или, например, по оси X или по оси Y .

2) вращательное движение

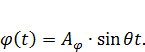(42)

В этом случае инерционная сила, соответствующая поступательному движению массы, будет равна;

.

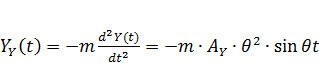Максимальное значение инерционной силы определяется из формулы

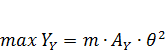(10)

Инерционный момент, соответствующий вращательному движению, будет равен:

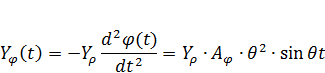
где 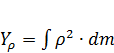– момент инерции массы.

Очевидно, что 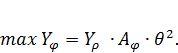(43)

Условимся в дальнейшем 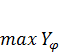записывать просто как .

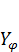Если на систему действуют две нагрузки (или две группы нагрузок), изменяющиеся по различным гармоническим законам

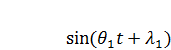и ,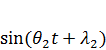

то в этом случае, применяя принцип независимости действия сил для произвольной системы, имеем:

(44)

где 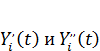- инерционные силы, соответствующие двум указанным законам (рис. 37).

Определив максимальные инерционные силы 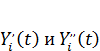от каждой нагрузки в отдельности. Легко получить, пользуясь выражением (44), следующую формулу для максимальной инерционной силы при суммарном воздействии нагрузок:

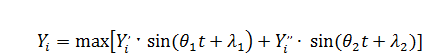(45)

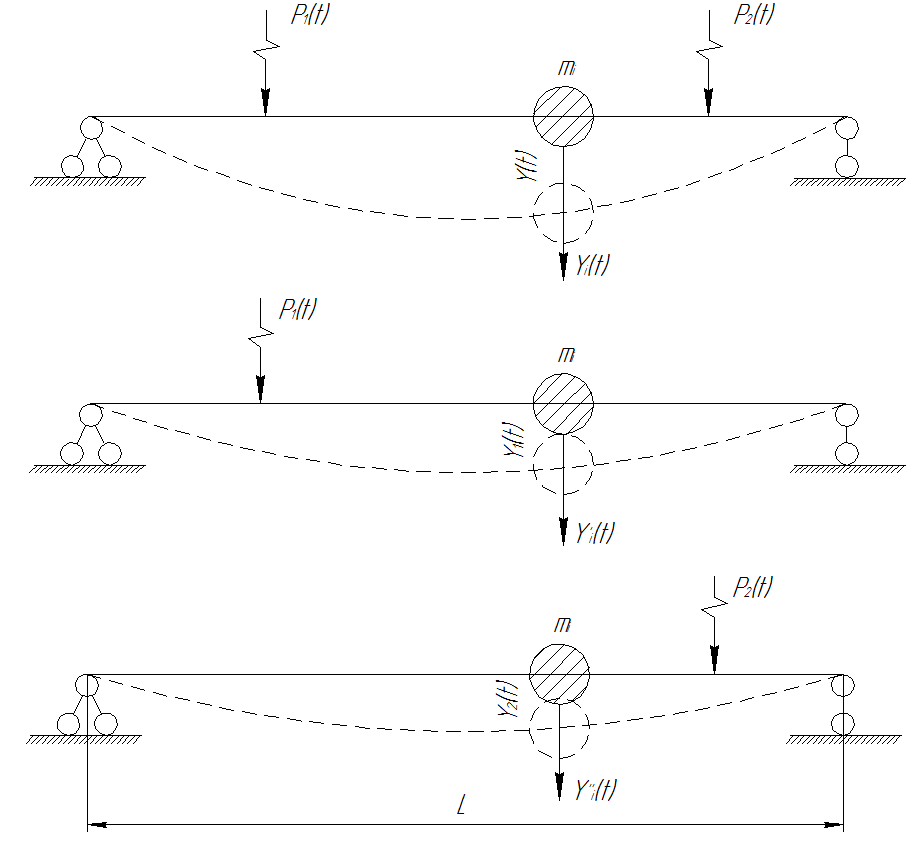
Рис. 37 Расчетная схема балки для определения максимальной инерционной силы

Когда на систему действует произвольная периодическая нагрузка, то такую нагрузку можно разложить в ряд Фурье и привести, таким образом, к простейшим гармоническим нагрузкам:

P(t)= 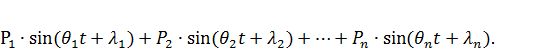(46)

В приближенных расчетах можно ограничиться первыми членами этого ряда и воспользоваться вышеизложенной методикой.

Как уже указывалось, значительные инерционные силы возникают при резонансе. В инженерных сооружениях резонанс недопустим. Однако и в этом случае отсутствия резонанса могут возникнуть инерционные силы, которые необходимо учитывать при расчете сооружения.

В связи с этим основными задачами динамики сооружений являются: 1) расчет сооружения на резонанс; 2) динамический расчет системы на действие максимальных возмущающих и инерционных сил.