Физическая кинетика. Явление переноса.
Если статистическая физика и термодинамика рассматривают равновесные состояния и процессы, то физическая кинетика изучает процессы, возникающие при нарушениях равновесия. Эти процессы являются необратимыми, т.к. система, выведенная из положения равновесия, стремится вернуться в равновесное состояние, что сопровождается ростом энтропии. Переход в равновесное состояние сопровождается также появлением потоков молекул, тепла и т.п. величин. Потоком некоторой величины называется количество этой величины, проходящее в единицу времени через некоторую реальную или воображаемую поверхность. Например, поток жидкости в трубе, поток света через окно, поток тепла через поверхность батареи и т.д. Явления, сопровождающиеся появлением потоков, получили название явленийпереноса, поскольку наличие потока означает перенос величины через некоторую воображаемую или реальную поверхность.
Каждое из явлений переноса обусловлено неодинаковостью значений в различных точках пространства некоторой величины 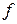 . Например, при диффузии такой величиной является концентрация молекул. Мы ограничимся рассмотрением случаев, когда величина
. Например, при диффузии такой величиной является концентрация молекул. Мы ограничимся рассмотрением случаев, когда величина 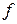 зависит только от одной координаты, например
зависит только от одной координаты, например 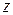 . Величину
. Величину 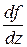 при рассмотрении явлений переноса обычно называют градиентом
при рассмотрении явлений переноса обычно называют градиентом 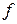 , хотя, фактически, эта величина является проекцией градиента на соответствующее направление.
, хотя, фактически, эта величина является проекцией градиента на соответствующее направление.
Рассмотрим три явления переноса: диффузию, внутреннее трение, теплопроводность, которые описываются эмпирическими уравнениями одного вида.
Диффузией называется обусловленное тепловым движением самопроизвольное выравнивание концентраций компонентов некоторой смеси.
Ограничимся рассмотрением двухкомпонентных смесей газов.
 Обозначим концентрации молекул одного и другого веществ
Обозначим концентрации молекул одного и другого веществ 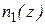 и
и 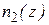 . Допустим, что вдоль оси
. Допустим, что вдоль оси 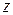 созданы градиенты концентраций
созданы градиенты концентраций
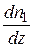 и
и 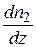 (11.3)
(11.3)
(рисунок 11.1). Чтобы исключить влияние на процесс выравнивания газодинамических потоков (т.е. макроскопических явлений типа ветра), будем считать, что давление вдоль выбранного направления (вдоль оси 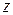 ) не изменяется. Поскольку
) не изменяется. Поскольку 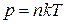 , то при постоянной температуре в объеме рассматриваемой системы, постоянной должна быть суммарная концентрация молекул смешивающихся веществ:
, то при постоянной температуре в объеме рассматриваемой системы, постоянной должна быть суммарная концентрация молекул смешивающихся веществ: 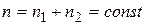 , поэтому градиенты концентраций должны быть связаны соотношением:
, поэтому градиенты концентраций должны быть связаны соотношением:
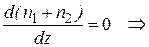
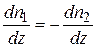 (11.4)
(11.4)
Экспериментально установлено, что в описанной ситуации через поверхность площадку S, перпендикулярную оси z , устанавливается поток молекул i-того сорта, равный:
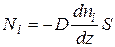 (11.5)
(11.5)
Коэффициент пропорциональности в (11.5) D называется коэффициентомдиффузии, а выражение (11.5) – закономФика.
Экспериментально установлено, что если в некоторой среде вдоль оси z создать градиент температуры 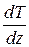 , то вдоль оси устанавливается поток тепла через площадку S, перпендикулярную оси z,:
, то вдоль оси устанавливается поток тепла через площадку S, перпендикулярную оси z,:
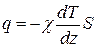 (11.6)
(11.6)
где c – коэффициенттеплопроводности. Соотношение (11.6) называют законом Фурье.
Если в жидкой газообразной среде создан градиент скорости ее слоев 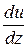 , то между слоями возникает сила трения.
, то между слоями возникает сила трения.
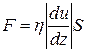 (11.7)
(11.7)
Здесь S – величина поверхности, по которой действует сила F.
По второму закону Ньютона взаимодействие с силой F можно рассматривать как результат передачи от одного слоя к другому в единицу времени импульса, т.е. существование потока импульса.
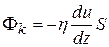 (11.8)
(11.8)
Минусы в правых частях уравнений (11.5), (11.6) и (11.8) отражают тот факт, что перенос соответствующих величин происходит в направлении их убывания.
Для того чтобы описать с МКТ точки зрения процессы переноса необходимо более детально представлять себе процессы взаимодействия молекул и связанные с этими процессами величины.
Дата добавления: 2017-01-26; просмотров: 2085;











