РЕЛЯТИВИСТСКОЕ ВЫРАЖЕНИЕ ДЛЯ ЭНЕРГИИ

Аналогично тому, как мы это делали при получении формулы 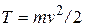можно и в релятивистской механике приравнять работу внешних сил изменению кинетической энергии частицы. При этом для кинетической энергии получается выражение:

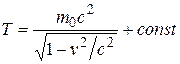(6.25)

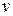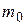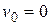- скорость движения частицы с массой покоя _. При кинетическая энергия должна обращаться в нуль. Следовательно, константа в (6.25) равна – 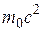, и для кинетической энергии справедлива формула:

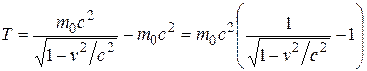(6.26)

Казалось бы, что свободной частице, движущейся со скоростью 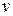, следует приписать полную энергию (6.26). Но оказывается, что сумма величин типа (6.26) при упругих столкновениях частиц не сохраняется. Это связано с тем, что свободная частица кроме кинетической энергии (6.26) обладает энергией покоя

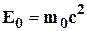. (6.27)

Соответственно полная энергия частицы оказывается равной

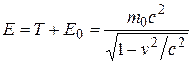. (6.28)

В случае сложного тела полная энергия включает в себя, кроме энергий покоя составляющих частиц, кинетическую энергию их движения относительно центра масс и потенциальную энергию взаимодействия частиц между собой.

Из выражений (6.23) и (6.28) вытекает связь между энергией и импульсом: 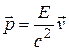и наоборот 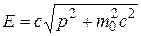(6.29)