Математические методы реконструкции изображений в трансмиссионной компьютерной томографии.

1) Метод, основанный на операциях свертки и обратного проецирования

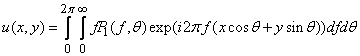(1)

Заменим область интегрирования в

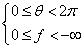
на более удобную для реализации алгоритма восстановления

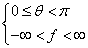(2)

используя свойство фурье-образа проекции Радона. В этом случае (1) можно представить в виде:

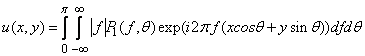. (3)

Двумерное обратное преобразование Фурье в полярных координатах, связанных с декартовыми координатами в частотной области соотношениями 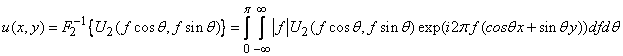(4)

Таким образом, чтобы по проекциям 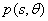восстановить функцию 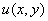, необходимо в соответствии с (3) выполнить определенную последовательность операций:

1) вычислить фурье-образ 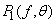проекции 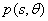по следующей формуле:

,

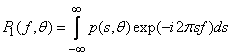которая с учетом ограниченных размеров исследуемых объектов имеет вид:

;

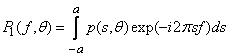2) умножить 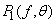на ;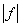

3) найти модифицированные проекции

,

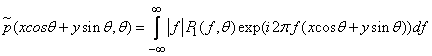вычислив обратное одномерное преобразование Фурье;

4) произвести интегрирование по углу :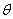

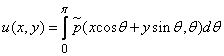. (5)

Очевидно, что операция, описываемая соотношением (5), является операцией обратного проецирования.

Для дискретных данных модифицированные проекции вычисляют с помощью одномерного БПФ. Интегрирование в (5) заменяют операцией суммирования по 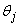. Следует отметить, что при вычислении оценки томограммы на дискретной прямоугольной сетке в четвертом пункте также применяют процедуру интерполяции. Однако эта интерполяция осуществляется не в частотной, как в фурье-алгоритме, а в пространственной области.