Клинические применения рентгеновской компьютерной томографии.

1972-1973гг ­­– Первые клинические испытания КТ – компьютерного рентгеновского томографа.

1979 г. Годфри Ньюболд Хаунсфилд и Алан Кормак за создание метода диагностики РКТ получили Нобелевскую премию.

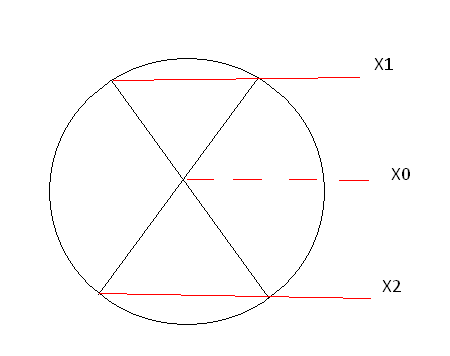Схематически метод можно представить следующим образом: при томографической регистрации изображения какого-либо слоя объекта источник излучения (например, рентгеновская трубка) движется прямолинейно или по кругу в плоскости Х₀ параллельно регистрируемому слою Х₁ над объектом. Регистрирующий материал, обычно фотопленка, движется позади объекта в плоскости Х₂, также параллельной к плоскости движения источника, по аналогичным траекториям, но в обратном направлении. Этим достигается стабилизация положения регистрируемого слоя на фотоматериале с одновременным размазыванием очертания других слоев.

Принцип КТ заключается в создании с помощью вычислительной машины послойных изображений исследуемого объекта на основе измерения коэффициентов линейного ослабления излучения, прошедшего через этот объект.

При рентгеновской КТ происходит послойное поперечное сканирование объекта коллимированным (суженным) пучком рентгеновского излучения. Излучение регистрирует система специальных детекторов с последующим формированием с помощью компьютера полутонового изображения на экране монитора.

Компьютерная томография (КТ) - современный метод лучевой диагностики, позволяющий получить послойное изображение любой области человека толщиной среза от 0,5мм до 10мм, оценить состояние исследуемых органов и тканей, локализацию и распространенность патологического процесса.

Билет 4.

Артефакты дискретного Фурье‐преобразования. Их обнаружение и устранение.

При численном нахождении преобразования Фурье следует очень внимательно относиться к таким важнейшим параметрам, как объем выборки и интервал дискретизации (Δ). Соотношение этих двух величин определяет диапазон частот (Ω0,ΩN), для которых возможно вычисление значений Фурье-спектра.

Влияние конечности интервала выборки

Определение преобразования Фурье - интеграл с бесконечными пределами. Его численное отыскание подразумевает принципиальную ограниченность интервала интегрирования. Влияние конечности интервала выборки проявляется главным образом на искажении его низкочастотной области. Спектр содержит довольно широкий максимум вместо одиночного пика, как было в случае средних частот сигнала.

Вместо спектра некоторой функции f(х) дискретное преобразование Фурье подразумевает вычисление спектра другой функции f(х)Ф(х), где Ф(х) — это функция-ступенька, равная единице в пределах расчетного интервала и нулю за его пределами. В частотной области это соответствует операции свертки означенных двух функций, что, конечно, искажает (неизвестный) точный спектр f(х).

Сдвиг ноль-линии

Добавление к сигналу ненулевой постоянной составляющей (так называемая сдвигом ноль-линии).

Избавиться от искажений, вызванных сдвигом ноль-линии, довольно просто. Достаточно (до Фурье-преобразования) вычислить среднее значение выборки и затем вычесть его из каждого элемента выборки.

Маскировка частот

Еще один пример ошибочного расчета Фурье-спектра связан с присутствием в сигнале гармоник с частотой, превышающей частоту Найквиста. В случае превышения частоты Найквиста в спектре начинают присутствовать "лишние" пики. Появление артефактов спектра связано с тем, что дискретных отсчетов начинает не хватать для того, чтобы прописать высокочастотные гармоники с достаточной информативностью.