Модели и их классификация

Мир, частью которого мы являемся, бесконечен, как бесконечен и любой объект, не только в пространстве и времени, но и в своих связях с другими объектами. В общем случае, модель - это некий объект – заместитель, который в определенной степени заменяет объект – оригинал, воспроизводя интересующие нас свойства и характеристики оригинала, причем по сравнению с оригиналом модель имеет существенные преимущества для определенного вида работы с ней, а именно: наглядность, доступность испытаний и т.п.

Большинство моделей являются абстрактными образами реального объекта, отражающими только те его свойства, которые интересуют человека в процессе познания или решения конкретной практической задачи.

Достаточно распространенная классификация моделей представлена на рисунке 1.2.

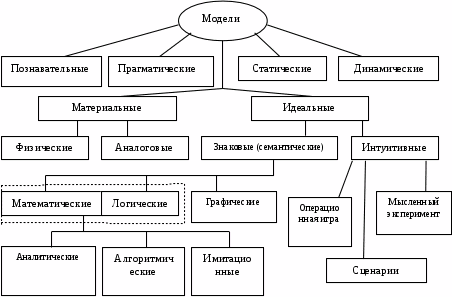
Рис. 1.2. Классификация моделей

Классификация моделей по назначению, целям моделирования.Если отвлечься от областей применения моделей, по целям моделирования их часто разделяют на2 основные типа: познавательные и прагматические. Такая дифференциация моделей соответствует делению целей моделирования на экспертные (теоретические) и конструктивные (практические). Наиболее наглядно разница между названными моделями проявляется в их отношении к оригиналу в процессе деятельности.

Познавательные модели предназначены для описания свойств или поведения реальных (существующих) объектов. Они являются формой организации и представления знаний, средством соединения новых знаний с имеющимися. Поэтому при обнаружении расхождения между моделью и реальностью встает задача устранения этого расхождения с помощью изменения модели. Фактически вся познавательная деятельность ориентирована, в основном, на приближении модели к объективной реальности, которую модель отражает.

Примерами познавательных моделей являются модели химических реакций, климатических проявлений, развития биологических популяций в природной среде, рассеивания веществ в атмосфере, разбавления примесей в руслах водотоков и других объектов и процессов, протекание которых обусловлено действием законов природы и не может быть как-то изменено человеком.

Прагматические модели (нормативные) выступают в качестве средства организации практических действий, рабочего представления целей системы для решения задач управления ею. Использование прагматических моделей состоит в том, чтобы при обнаружении расхождения между моделью и реальностью направить усилия на изменение реальности, чтобы приблизить реальность к модели, к достижению целей, ей задаваемых.

Примерами прагматических моделей (рис. 1.3) могут служить планы, программы и сценарии действий в определенной сфере, модели систем управления экономикой страны, модели производственных и других объектов как объектов проектирования и управления, модели технологических процессов.

человек

человек

Модель

Реальный объект

Прагматическая модель Цель: практическая

Познавательная модель Цель: теоретическая

Рис. 1.3. Познавательная и прагматические модели

Познавательные модели отражают существующие, а прагматические - хоть и не существующие, но желаемые и, возможно, исполнимые отношения и связи.

Классификация моделей по учету фактора времени.По характеру учета фактора времени модели делятся на статические и динамические.

При формировании статической модели предполагается, что все зависимости относятся к одному моменту времени, а моделируемая система неизменна во времени. В данном случае игнорируются возможные изменения, т.к. их учет не требуется для достижения цели моделирования. Кроме того, предполагается, что все интересующие процессы, происходящие в системе не требуют при своем описании развертывания во времени.

Динамические модели отображают текущее или желаемое состояние объекта во времени, т.е. процесс изменения состояний реальной или проектируемой системы, развитие событий с течением времени.

Классификация моделей по способу моделирования.По способам моделирования модели делят на материальные и идеальные.

К материальным относят модели, воспроизводящие основные геометрические, физические, динамические и функциональные характеристики изучаемого объекта.

Идеальная (информационная) модель – это модель, построенная на основе абстрактных образов объекта моделирования с использованием чисто функциональной аналогии, а не на основе его материализованной аналогии. Это совокупность информации, характеризующей свойства и состояния объекта, процесса, явления, а также его взаимосвязь с внешним миром.

Идеальное (информационное) моделирование имеет теоретический характер.

Материальные модели. Материальные модели могут быть физическими и аналоговыми.

Физическими принято называть модели, которые реальному объекту противопоставляют его уменьшенную (реже увеличенную) копию, пригодную для лабораторного исследования и позволяющую переносить установленные свойства на реальный объект с помощью теории подобия.

Аналоговое моделирование основано на аналогии процессов и явлений, имеющих различную физическую природу, но описываемую формально одними и теми же математическими уравнениями, логическими схемами и т.п.

Например, электрические цепи представляет собой совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, токе и напряжении. Поскольку процессы в электрических цепях являются аналогами многих химических, механических и биологических процессов, электрические цепи могут быть использованы для моделирования таких процессов.

Идеальные (информационные) модели.Идеальные (информационные) модели состоят из интуитивных и знаковых (семантических).

Интуитивные модели. Интуитивные модели формируются на основе предшествующего опыта, наблюдения и воображения специалистов о моделируемом объекте. Принципиальная особенность интуитивных моделей – это отсутствие их логического обоснования. Интуитивные модели, как правило, используются на первоначальном этапе исследования объекта либо в том случае, когда с помощь других видов моделей описать объект не представляется возможным.

Сценарные модели подробно описывают набор предполагаемых состояния системы (ситуаций, сцен), характеристики каждого элемента в этих состояниях.

Игровые модели рассматривают процессы, в которых участвуют несколько сторон, реализующих свои интересы. Каждая из сторон имеет свою цель и использует для этого определенную линию поведения в зависимости от действий других сторон. Игровые модели помогают выявить проблемные ситуации, которые могут возникнуть в реальных условиях, проанализировать их и выбрать пути их решения.

Мысленные модели представляют собой образы моделируемой системы, которые находят отражение в человеческом сознании. В зависимости от потребностей данный класс моделей может принимать различные виды, которые только отражают окружающую действительность (мысленная фотография) или более глубоко представляют систему на уровне понятий, суждений, умозаключений (т.е. в форме, которую реально наблюдать нельзя). По существу человек представляет окружающий мир в виде мысленных моделей, так как всякая мысль есть результат отражения того, что нас окружает. Каждый мыслящий человек пользуется этими моделями.

Для словесных моделей характерны широкое применение аналогий, правдоподобных рассуждений. Однако многозначность понятий в них затрудняет проведение расчетов и приводит к громоздким записям. Для устранения этих недостатков целесообразно использовать знаковые модели.

Знаковые (семантические модели).Знаковая модель воспроизводит моделируемый объект с помощью знаков. Знаковые модели обычно подразделяют на:

– математические,

– логические и

– графические.

Математическая модель определяется как заместитель реального объекта, обеспечивающий изучение его свойств, как совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности, присущие изучаемому процессу, объекту или системе, исследование которых средствами математики должно ответить на поставленные вопросы.

Математическая модель – это строго формализованное на языке математики описание исследуемого объекта (системы). Такая модель нужна для того, чтобы:

– понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание);

– научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);

– прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

В основе логических моделей лежит описание объекта, системы, процесса (предметной области) в виде некоторого множества утверждений, выраженных в виде логических формул с получением решения построением вывода в некоторой формальной (дедуктивной) системе.

Математические и логические модели в зависимости от стоящей перед исследователем задачи могут быть:

– аналитическими,

– алгоритмическими и

– имитационными.

Аналитическая модель - это совокупность математических зависимостей, построенных на принципах формального подобия процессов, происходящих в объекте.Ваналитическихмоделяхповедение сложной системы записывается в виде некоторых функциональных соотношений или логических условий.

Алгоритмическая модель — математическая модель, представленная в форме алгоритма, перерабатывающего заданный набор входных данных в заданный набор выходных данных.

Имитационная модель – универсальное средство исследования сложных систем, представляющее собой логико-алгоритмическое описание поведения отдельных элементов системы и правил их взаимодействия, отображающих последовательность событий, возникающих в моделируемой системе. Имитационное моделирование – это метод исследования, заключающийся в имитации на ЭВМ с помощью комплекса программ процесса функционирования системы или отдельных ее частей и элементов.

Предметом рассмотрения в данном учебном пособии является применение математических моделей для решения задач эколого-экономического проектирования и управления производственно-хозяйственными объектами и. в частности, объектами химической и нефтегазохимической отрасли. Решение таких задач предполагает:

– изучение объекта;

– постановку (формулировку) задачи;

– выбор (разработку) методов ее решения;

– разработку и актуализацию математических моделей (создание формализованного описания объекта);

– выбор (разработку) средств для поиска оптимальных решений с использованием разработанных моделей;

– решение задач оптимизации;

– анализ результатов полученных решений;

– применение полученных результатов на практике.