Частота вращения магнитного потока ротора
Так как в короткозамкнутом роторе каждый стержень (в пазу проводника) образует отдельную фазу, а пазы ротора сдвинуты в пространстве, то сдвинутые по фазе токи в стержнях создают вращающееся магнитное поле. В любом случае частота вращения магнитного потока ротора в пространстве равна сумме частоты вращения самого ротора 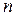 и частоты вращения потока ротора относительно ротора
и частоты вращения потока ротора относительно ротора 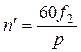 , т.е.
, т.е. 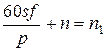 . Таким образом, магнитные потоки статора и ротора вращаются относительно статора с одинаковой частотой
. Таким образом, магнитные потоки статора и ротора вращаются относительно статора с одинаковой частотой 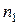 и образуют один результирующий магнитный поток.
и образуют один результирующий магнитный поток.
11.8. Уравнения магнитодвижущих сил и ток статора
асинхронного двигателя
При холостом ходе асинхронного двигателя МДС ротора близка к нулю и вращающийся магнитный поток создается только МДС статора
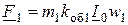 ,
,
где 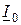 – ток холостого хода двигателя.
– ток холостого хода двигателя.
При увеличении нагрузки на валу двигателя увеличивается ток ротора, а его МДС
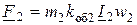 .
.
Геометрическая сумма МДС статора и ротора всегда равна МДС статора при холостом ходе
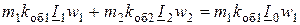 .
.
Отсюда
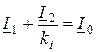 (11.19)
(11.19)
или
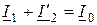 , (11.20)
, (11.20)
где 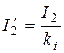 – приведенный ток ротора. (11.21)
– приведенный ток ротора. (11.21)
Здесь 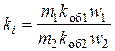 – коэффициент трансформации по току.
– коэффициент трансформации по току.
Из (11.20) ток статора двигателя
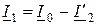 . (11.22)
. (11.22)
Уравнения токов (11.20) и (11.22) аналогичны соответствующим уравнение для токов трансформатора. Ток статора, как и ток первичной обмотки трансформатора, имеет составляющие тока холостого хода и ток ротора, обусловленный нагрузкой. Отличие заключается в том, что ток холостого хода асинхронного двигателя намного больше, чем в трансформаторе, и составляет 40…60 % от номинального значения. Это обусловлено двойным воздушным зазором в магнитной системе машины.
Составляющая тока ротора 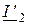 появляется тогда, когда к валу ротора приложен тормозной момент. При этом приведенный ток
появляется тогда, когда к валу ротора приложен тормозной момент. При этом приведенный ток 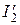 отличается от реального не только за счет разного числа витков и обмоточных коэффициентов обмоток статора и ротора, но и числа фаз обмоток ротора. Поэтому для приведения ротора необходимо, чтобы
отличается от реального не только за счет разного числа витков и обмоточных коэффициентов обмоток статора и ротора, но и числа фаз обмоток ротора. Поэтому для приведения ротора необходимо, чтобы 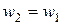 ,
, 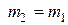 ,
, 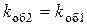 , что было учтено в (11.20).
, что было учтено в (11.20).
11.9. Схема замещения и векторная диаграмма асинхронного двигателя
При анализе работы асинхронной машины используют схему замещения. Переход от схемы с электромагнитной связью к схеме с электрической связью показан на (рис. 11.6). На схеме замещения (рис. 11.6 а) электромагнитная связь осуществляется через основной магнитный поток 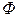 , который индуктирует в обмотке статора ЭДС
, который индуктирует в обмотке статора ЭДС 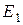 , а в обмотке вращающегося ротора – ЭДС
, а в обмотке вращающегося ротора – ЭДС 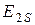 , определяемые уравнениями (11.5) и (11.8). Схема замещения (рис. 11.6 б) соответствует неподвижному ротору, для которого индуктивное сопротивление равно
, определяемые уравнениями (11.5) и (11.8). Схема замещения (рис. 11.6 б) соответствует неподвижному ротору, для которого индуктивное сопротивление равно 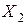 , активное –
, активное – 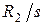 . При этом ЭДС ротора
. При этом ЭДС ротора 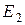 определяется выражением (11.9), а уравнение электрического равновесия для цепи ротора имеет вид
определяется выражением (11.9), а уравнение электрического равновесия для цепи ротора имеет вид
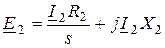 . (11.23)
. (11.23)
Умножив это равенство на коэффициент трансформации ЭДС 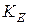 (11.11) с учетом (11.12) и (11.21) получим
(11.11) с учетом (11.12) и (11.21) получим
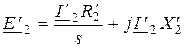 , (11.24)
, (11.24)
где 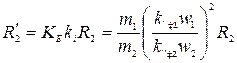 – приведенное активное сопротивление фазы ротора;
– приведенное активное сопротивление фазы ротора; 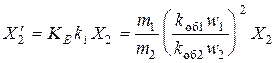 – приведенное индуктивное сопротивление фазы ротора.
– приведенное индуктивное сопротивление фазы ротора.
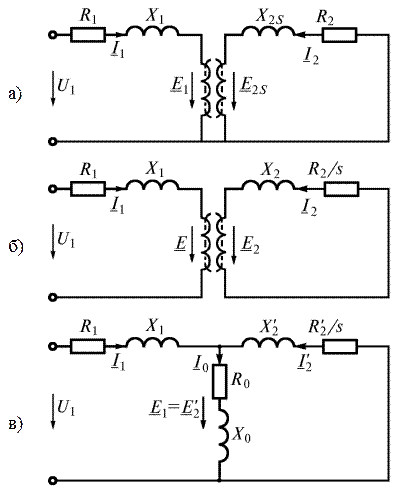
Рис. 11.6
Уравнение (11.24) позволяет перейти к схеме замещения (рис. 11.6. в) с электрической связью между статором и ротором. В ветви намагничивания протекает ток 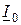 , который согласно (11.20) и схеме замещения
, который согласно (11.20) и схеме замещения
(рис. 11.6 в) определяется по формуле
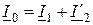 .
.
Падения напряжения от этого тока на сопротивлениях 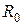 и
и 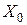 равны ЭДС:
равны ЭДС: 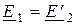 .
.
Уравнение электрического равновесия для цепи статора
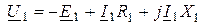 (11.25)
(11.25)
аналогично уравнению (9.7) для первичной цепи трансформатора.
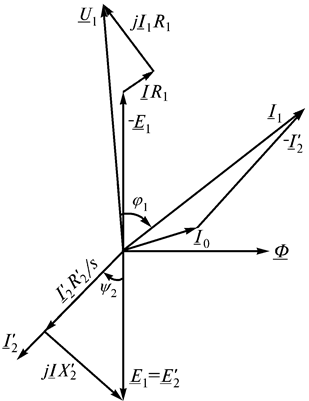 Рис. 11.7
Рис. 11.7
|
Схеме замещения (рис. 11.6 в) и уравнениям (11.24) и (11.25) соответствует векторная диаграмма (рис. 11.7). Из рис. 11.18 видно, что с увеличением момента нагрузки на валу и, следовательно, скольжения, возрастает ток ротора 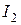 . Из векторной диаграммы следует, что одновременно увеличивается ток статора
. Из векторной диаграммы следует, что одновременно увеличивается ток статора 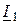 и уменьшается фаза
и уменьшается фаза 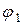 . С увеличением тока
. С увеличением тока 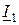 увеличиваются падения напряжения
увеличиваются падения напряжения 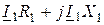 на статоре и когда падение напряжения становится соизмеримым с напряжением
на статоре и когда падение напряжения становится соизмеримым с напряжением 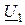 , угол
, угол 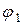 вновь возрастает.
вновь возрастает.
В режиме холостого хода ток ротора 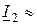 0, угол сдвига
0, угол сдвига 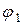 тока статора относительно напряжения сети
тока статора относительно напряжения сети 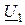 близок к
близок к 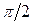 .
.
Дата добавления: 2017-01-16; просмотров: 3043;











