Поля в направляющих системах
Пусть все составляющие электромагнитного поля в направлении координаты Z изменяются по закону 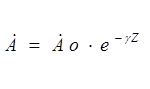 ,
,
где 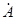 - любая составляющая векторов
- любая составляющая векторов 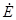 и
и 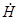 ,
,
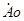 - начальная составляющая векторов
- начальная составляющая векторов 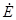 и
и 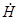 ,
,
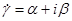 - коэффициент расширения волны в направляющей системе,
- коэффициент расширения волны в направляющей системе,
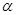 - коэффициент затухания,
- коэффициент затухания,
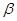 - коэффициент фазы волны в направляющей системе.
- коэффициент фазы волны в направляющей системе.
Первая и вторая производные любой из составляющих по координате Z равны 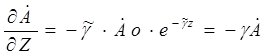
Волновое уравнение 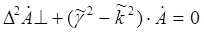
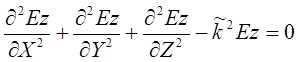 |
Волновое уравнение в прямоугольной системе координат для составляющей Ez будет записано как
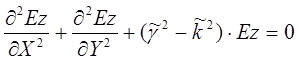 |
или
Обозначим 
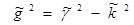 ,
,
где g – поперечный волновой коэффициент или поперечная составляющая волнового числа..
Если потери в системе малы, тогда

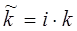 ,
, 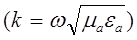 ,
, 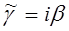
получим 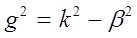
Решив уравнение для продольной составляющей Ez и Hz в зависимости от типа волны, поперечные составляющие находят через продольные из уравнения Максвелла.
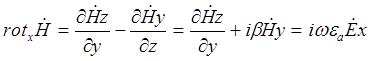 (1)
(1)
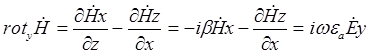 (2)
(2)
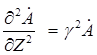 |
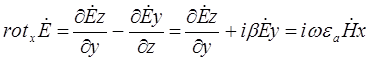 (3)
(3)
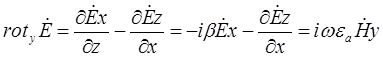 (4)
(4)
Решая уравнение (1) и (4) получаем Ex и Hy, а из уравненй (2) и (3) находим Ey и Hx.
Рассмотрим получение Ex.
Выразим Hy из уравнения (1) и подставим в уравнение (4). Получим
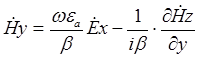
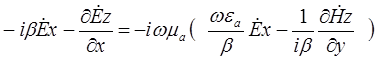
домножим всё уравнение на 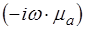 . В результате получим:
. В результате получим:
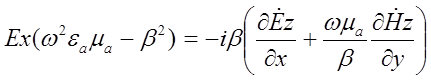 |
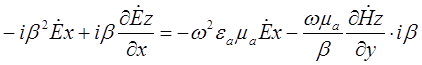
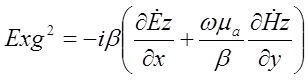 |
Проведя аналогичные преобразования можно получить уравнения для 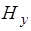 из (1) и (4) уравнений, и для
из (1) и (4) уравнений, и для 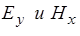 из (2) и (3) уравнений.
из (2) и (3) уравнений.
В итоге получим следующую систему уравнений:
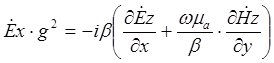 (5)
(5)
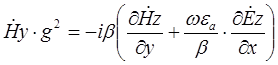 (6)
(6)
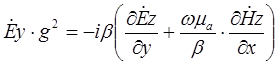 (7)
(7)
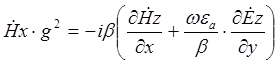 (8)
(8)
Дата добавления: 2017-01-16; просмотров: 2092;











