Электрический заряд. Закон сохранения заряда изолированной системы. Закон Кулона.

На предыдущих лекциях мы уже касались вопроса о взаимодействии между атомами или молекулами вещества (силы упругости, основные положения МКТ и др.). Что это за взаимодействия? Чем оно обусловлено и каковы их особенности? Эти и другие вопросы будут занимать наше внимание в разделе «Электромагнетизм».

Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.

Электрический заряд – это мера участия тел в электромагнитных взаимодействиях.

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

•Существует два рода электрических зарядов, условно названных положительными и отрицательными.

• Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

· Одноименные заряды отталкиваются, разноименные – притягиваются (рис. 1).

· В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда:

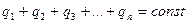(1)

Закон сохранения электрического заряда утверждает, что в изолированной

Рис.1 системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Т. е. электрический заряд тела – дискретная величина, равная: .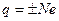

Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

Носителями электрического заряда в природе являются 2 элементарные частицы: протон и электрон:

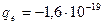Кл ; Кл .

Точечным зарядом называется заряженное тело, размером которого в условиях данной задачи можно пренебречь.

Силу взаимодействия между элементарными точечными зарядами определяется законом Кулона:

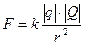, (2)

где r – расстояние между зарядами, .

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.

Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел. Рис. 2 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.

Рис. 2 2. Электрическое поле. Напряженность. Напряженность поля точечного заряда. Принцип суперпозиции полей.

Взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле – это особая форма материи, посредством которой осуществляется взаимодействие между заряженными частицами.

Неподвижный заряд создает статическое поле, которое действует на второй заряд. Силовой характеристикой электростатического поля является его напряженность.

Напряженность это величина равная отношению силы, действующей со стороны поля на заряд, помещенный в данную точку поля к величине этого заряда:

. (3)

Напряженность электрического поля – векторная физическая величина. Направление вектора напряжённости совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

Пробным называют небольшой по величине точечный заряд, который не вносит заметного перераспределения сил взаимодействия рассматриваемых зарядов.

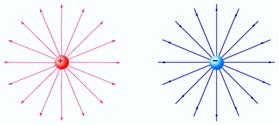
Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора в каждой точке совпадало с направлением касательной к силовой линии (рис. 3).

Силовыми линиями называется геометрическое место точек касательные к которым совпадают с вектором .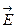

Рис.3 При этом густота должна быть пропорциональна модулю вектора напряженности поля.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рис. 4.

Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим

Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор 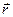от заряда Q к точке наблюдения.

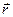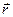Тогда при Q > 0 вектор параллелен , а при Q < 0 вектор противоположен . Рис. 4

Выражение для определения напряжённости поля точечного заряда в векторной форме имеет вид:

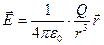, (4)

где r – модуль радиус-вектора .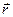

Модуль вектора напряженности поля точечного заряда Q:

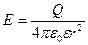, (5)

где Q – заряд, создающий поле; 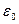- электрическая постоянная 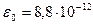Ф/м; r – расстояние от заряда Q до точки; - диэлектрическая проницаемость среды.

В случае, когда поле создается системой из n зарядов, его напряженность определяется принципом суперпозиции полей.

Напряженность поля системы зарядов равно векторной сумме напряженностей полей каждого из зарядов системы

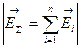. (6)

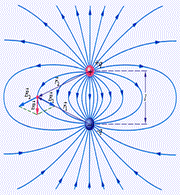
В качестве примера применения принципа суперпозиции полей, на рис. 5 изображена картина силовых линий поля электрического диполя – системы из двух одинаковых по модулю зарядов разного знака q и –q, расположенных на некотором расстоянии.

Рис. 5 3. Потенциал поля. Потенциал поля точечного заряда. Работа по перемещению заряда в электрическом поле.

Энергетической характеристикой электрического поля является его потенциал.

Потенциалом называется величина равная отношению потенциальной энергии заряда, помещенного в данную точку поля к величине этого заряда.

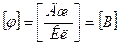(7)

Если поле создается системой, то потенциал поля системы равен алгебраической сумме потенциалов полей зарядов, составляющих данную систему .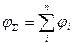

При перемещении заряда из одной точки пространства в другую поле совершает работу равную убыли потенциальной энергии заряда.

;

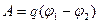но т.к. , то . (8)

Величина 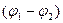называется разностью потенциалов. Ее физический смысл: это работа поля по перемещению единичного положительного заряда из одной точки поля в другую.

Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом.

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Таким образом потенциал поля точечного заряда определяется:

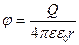, (9)

где Q – заряд, создающий поле; r – расстояние до точки Q.

Для определения связи между 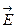и 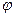, рассмотрим работу поля по перемещению заряда q с силовой и с энергетической точек зрения

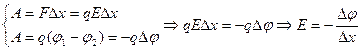, (10)

т.е. напряжённость электрического поля равна градиенту потенциала.

Знак (−) указывает на то, что напряженность направлена в сторону убывания потенциала (рис.6).

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 6 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.

Рис. 6

<== предыдущая лекция | следующая лекция ==>
Измерение сопротивлений. | 

Дата добавления: 2017-01-16; просмотров: 2248;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.014 сек.