Релятивистское обобщение модели Бора.
Выше мы уже обращали внимание на то, что в тяжелых водородоподобных системах ( Z >> 1) электрон становится релятивистским, т.е. нашей модели уже недостаточно. Рассмотрим теперь релятивистское обобщение модели Бора. Так же как и раньше, ограничимся случаем круговых орбит. Запишем релятивистское уравнение движения в виде
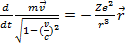 (15.29)
(15.29)
Поскольку на круговой орбите модуль вектора скорости остается постоянным, уравнение (4.29) можно переписать в виде
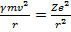 (15.30)
(15.30)
Здесь 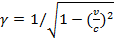 - релятивистский фактор. Фактически уравнение движения (15.30)
- релятивистский фактор. Фактически уравнение движения (15.30)
отличается от нерелятивистского случая (15.11) появлением множителя γ .
Будем также считать, квантовое условие Бора (15.12) верно и при релятивистских
скоростях. Тогда имеем:
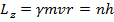 (15.31)
(15.31)
Опять имеем два уравнения (15.31) и (15.30) для определения радиусов орбит и соответствующим им скоростей движения. После несложных преобразований получаем
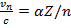 (15.32)
(15.32)
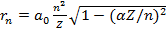 (15.33)
(15.33)
Отметим, в частности, что выражения для скорости движения по орбите, полученные в релятивистском и нерелятивистском случаях, совпадают. Найдем теперь энергию электрона на орбите. Поскольку при движении в кулоновском поле
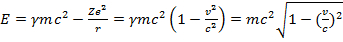 (15.34)
(15.34)
получим
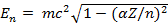 (15.35)
(15.35)
Может быть, наиболее удивительным является то, что решение задачи существует не для любых Z . Как видно из (15.33) и (15.35) для основного состояния системы ( n = 1) полученные выражения теряют смысл для сверхтяжелых ядер с зарядом больше некоторого критического Z * :
Z>Z*=1/ 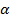 =137
=137
(15.36)
При Z = Z * = 137 полная энергия электрона (включая энергию покоя) обращается в
ноль, а орбита имеет нулевой радиус. Для ядер с большим зарядом устойчивой орбиты,
соответствующей случаю n = 1, в рамках модели Бора найти нельзя. То есть модель Бора
фактически предсказывает существование конца таблицы Менделеева. Интересно, что
точно такой же ответ получается и в рамках релятивистской квантовой теории, базирующейся на решении волнового уравнения Дирака17. Проверить сделанные предсказания напрямую вряд ли возможно, поскольку синтезировать ядра со столь большим значением Z (необходимо еще электронную оболочку создать) в настоящее время проблематично.
Чуть более подробно остановимся теперь на случае небольших значений Z и рассмотрим вопрос о релятивистских поправках к энергетическим уровням атома водорода и водородоподобных ионов. Отметим, прежде всего, что в выражение (3.48) включена также энергия покоя электрона, которую мы не учитывали в рамках нерелятивистской теории. Поэтому для сравнения результатов и нахождения релятивистских поправок перепишем выражение (15.35), исключив из него энергию покоя
s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz-cs w:val="24"/></w:rPr><m:t>)</m:t></m:r></m:e></m:rad></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 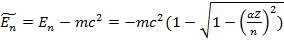 (15.37)
(15.37)
Проводя в (15.37) разложение корня в ряд Тейлора, получаем
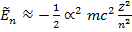 (15.38)
(15.38)
что, как нетрудно видеть, совпадает с выражением (15.22). Релятивистская поправка к
энергии δEp получается при учете второго члена разложения корня в (15.37):
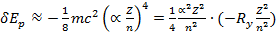 (15.39)
(15.39)
Например, для основного состояния атома водорода имеем
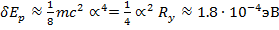 (15.40)
(15.40)
Корпускулярно-волновой дуализм.
Свет от точечного монохроматического источника, падал на два небольших отверстия на экране. Эти отверстия действуют как два когерентных источника света S1 и S2. Волны от них интерферируют в области перекрытия, проходя разные пути: ℓ1 и ℓ2
Вывод: На экране наблюдается чередование светлых и темных полос
В 1924 году Л. де Бройль4 высказал предположение, что такой дуализм «волна –
частица» присущ не только фотонам, но и всем другим микрообъектам – электронам и другим частицам. Движению частицы в пространстве соответствует некоторый волновой процесс: частице с импульсом 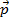 соответствует волна (мы будем называть ее волной де Бройля) с волновым вектором k (длиной волны λD = 2π/k ) и частотой ω, причем связь этих величин с импульсом и энергией частицы определяется соотношениями:
соответствует волна (мы будем называть ее волной де Бройля) с волновым вектором k (длиной волны λD = 2π/k ) и частотой ω, причем связь этих величин с импульсом и энергией частицы определяется соотношениями:
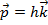 ,
, 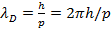 ,
, 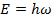 (16.1)
(16.1)
где v - скорость частицы. В нерелятивистском пределе (а в дальнейшем для нас, как правило, будет важен именно этот случай) имеем
 (16.2)
(16.2)
Оценим величину длины волны де Бройля для электрона с энергией в несколько элек-
тронвольт (характерный масштаб энергий в атомной физике). Мы получаем величину
порядка ангстрема. Именно вследствие малости этой величины наблюдать эксперимен-
тально волновые свойства электрона непросто. Характерный размер пространственной
структуры для наблюдения дифракции должен быть порядка длины волны, т.е. тоже
иметь масштаб в несколько ангстрем. Именно такой размер имеют расстояния между
атомами в твердых телах. Поэтому монокристалл образует своеобразную дифракцион-
ную решетку, которая может быть использована для обнаружения волновых свойств
электронов. Такие опыты впервые были выполнены К.Девиссоном6 и Л.Джермером7 в
1927 году и доказали блестящее совпадение гипотезы де Бройля с экспериментальными
данными. Экспериментальная схема установки, использованная Девиссоном и Джерме-
ром для наблюдения дифракции электронов, приведена на рис.5.1. Пучок электронов,
сформированный в электронной пушке (А) и ускоренный разностью потенциалов V (эта
величина составляла несколько десятков вольт) падал на кристалл никеля под некоторым углом θ. Детектор (С) измеряет интенсивность рассеянного пучка в зависимости от
угла рассеяния и энергии ускоряемых электронов. Оказалось, что полученные данные
очень похожи на те, которые получаются при дифракции рентгеновских лучей на моно-
кристаллах. Как известно, положение максимумов в спектре отраженного от кристалла
излучения может быть найдено из условия Вульфа-Брэгга
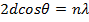 (16.3)
(16.3)
где d - расстояние между плоскостями решетки, λ - длина волны излучения, n - номер
соответствующего максимума. В случае электронного пучка под длиной волны следует
понимать длину волны де Бройля, которую в рассматриваемом случае можно записать в
виде
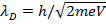 (16.4)
(16.4)
| Рис 16. 1 |
 (16.5)
(16.5)
A - некоторая константа, не зависящая от параметров пучка электронов и кристаллической
решетки. Именно соотношение (16.5) было проверено экспериментально. Типичная зависимость интенсивности рассеянного пучка электронов от его энергии (угол рассеяния полагается неизменным) приведена на рис.16.1.
Положение максимумов на кривой оказалось соответствующим выражению (16.5), т.е. пучок электронов действительно вел себя как волновое поле, характеризующееся длиной волны де Бройля. Дифракция пучка электронов при прохождении через поликристаллическую
структуру наблюдалась в 1930 году в экспериментах Дж.П.Томсона.8. Эти опыты также
подтвердили справедливость соотношения (16.5).
| Рис 16. 2 |
же понять, почему волновые свойства макрообъектов практически всегда ненаблюдаемы.
Итак, подведем некоторые итоги.
Всем микрообъектам присущи как волновые, так и корпускулярные свойства. Их
движение в пространстве должно описываться волновой теорией. Соответствующее
волновое поле распределено в пространстве и, в соответствии с классической волновой
теорией, в дифракционных опытах распространяется сразу через две (а может и не-
сколько) щелей. Однако при измерении микрочастица регистрируется в некоторой
точке пространства, как единое целое со всеми присущими этой частице характери-
стиками (массой, зарядом, энергией и т.п.). Результат измерения носит вероятност-
ный характер, предсказать, где будет обнаружена частица с достоверностью едини-
ца, вообще говоря, невозможно. Можно говорить лишь о вероятности того или иного
события и эта вероятность, в конечном счете, определяется волновым полем, которое
описывает движение частицы в пространстве. Получается, что в интерференционных
опытах частица, оставаясь неделимой или нерасщепляемой, способна проходить сразу
через две (несколько) щелей.
Выделенный курсивом текст представляет собой основу концепции корпускулярно-волнового дуализма.
Отметим, правда, одно интересное обстоятельство. Хотя многочисленные эксперименты показывают, что отдельным частицам (фотонам, электронам) присущи как корпускулярные, так и волновые свойства, когда мы говорим об электромагнитном излучении, мы обычно говорим о волновом поле, которое при определенных условиях проявляет корпускулярные свойства. Наоборот, когда мы говорим об электронах, то обычно имеем в виду частицы, которым, бывает, присущи и волновые свойства. Для ансамбля частиц возникает некоторая асимметрия в описании. Причину ее возникновения мы обсудим позже (см. Л_10), когда будем говорить о связи спина (собственного механического момента) со статистическим описанием ансамбля большого количества частиц.
Для лучшего понимания сути концепции корпускулярно-волнового дуализма вернемся снова к дифракционному опыту с двумя щелями, однако, вместо фотонов рассмотрим теперь прохождение через щели электронов. В случае, если открыта одна из щелей, на экране будут возникать плавные распределения, описывающее распределение электронов (Р1 или Р2 – см. рис.2.7). При открытых обеих щелях на экране возникнет интерференционная картина Р12. Попытаемся теперь узнать, не закрывая отверстия, через которое из них пролетел электрон. Для этого введем в систему дополнительную «измерительную аппаратуру». Например, около каждой из щелей мы поставим по лампочке. Рассеивая излучаемый лампочкой свет (для его регистрации мы будем использовать расположенные рядом детекторы D1 и D2), электрон обнаружит свое местоположение, и мы точно узнаем, через какую из щелей он проскочил. Однако, оказывается, интерференция исчезнет! На экране возникнет распределение Р=Р1+Р2, соответствующее ситуации, когда статистика набиралась при поочередно открытых щелях. Получается, что когда мы «смотрим» на электроны, они ведут себя иначе! В общем это можно понять: свет, рассеиваясь на электронах, «толкает» их и тем самым искажает процесс. Будем убавлять яркость, чтобы уменьшить воздействие света на пролетающие электроны. Но здесь скажется квантовая природа излучения: начиная с определенного момента времени, мы заметим, что интенсивность отдельных световых вспышек, свидетельствующих о пролете электрона, уже не меняется, но некоторые электроны проскакивают незамеченными.
Они достигли экрана, но ни один из детекторов их не зарегистрировал. Это понятно: источник излучения стал настолько слаб, что в момент пролета электрона через систему щелей, в этой области пространства не оказалась ни одного фотона, который мог бы рассеяться на пролетающем мимо электроне. Кажется удивительным другое: именно в этот момент на экране начинает возникать интерференционная картина. Незамеченные электроны характеризуются распределением Р12. Можно пойти другим путем: убавим импульс фотонов, возмущающих движение электронов. Это просто осуществить, если 
Рис 16. 3
использовать излучение более длинноволнового диапазона частот. И тогда толчки электронов будут слабее, степень влияния нашей «измерительной аппаратуры» будет мала. Однако и на этом пути нас ждет неудача. Мы знаем, что предельная разрешающая способность оптической аппаратуры составляет величину порядка длины волны λ . Это значит, что как только длина волны используемого света окажется больше расстояния между щелями d ( λ ≥ d ), зарегистрировав электрон, мы не сможем сказать через какую из щелей он пролетел. И опять, именно в этот момент появится интерференционная картина. Получается, что надо выбирать одно из двух: либо мы наблюдаем интерференционную картину, но тогда мы не знаем, через какую из щелей прошел тот или иной электрон, либо мы имеем эту информацию, но тогда интерференционной картины не будет.
Покажем, что в этом последнем утверждении нет ничего таинственного. Воздействие на электрон рассеиваемого на нем фотоне действительно должно привести к замыванию интерференционной картины. Действительно, длина волны рассеиваемого света λ должна быть меньше расстояния между щелями, т.е. λ < d . Тогда для импульса фотона имеем p = 2πh λ > 2πh d . Этот импульс при рассеянии передается электрону и толкает его вбок, т.е.
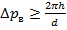 (16.5)
(16.5)
В результате электрон отклонится на угол θ , равный
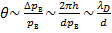 (16.6)
(16.6)
где λD - длина волны де Бройля. Но полученная величина как раз соответствует значению угла, под которым виден первый минимум интерференционной картины. То есть картина действительно размоется.
На этом примере рассмотрим вопрос о роли «измерительного прибора» и процедуры изменения в микромире. Мы, конечно, понимаем, что процедура измерения какой-либо физической величины всегда требует ввода в рассматриваемую систему «измерительного прибора», а сама процедура измерения как раз и происходит в результате взаимодействия исследуемого объекта с «измерительным прибором». Мы привыкли, и нам очень хочется считать, что это всегда возможно, что обратное воздействие измерительного прибора на исследуемый объект может быть сделано пренебрежимо малым. То есть физический процесс в отсутствие «измерительного прибора» и при его наличии развивается одинаково. Но это не так. В микромире атомно-молекулярных масштабов таким обратным влиянием «прибора» пренебречь нельзя. Появление в системе «измерительного прибора» меняет физическую систему и заставляет ее эволюционировать иначе, чем в отсутствие измерения.
В том, что существует такая разница между измерениями в микро- и макромире нет ничего удивительного. Рассмотрим, например, процедуру измерения скорости микро- и макрообъекта (например, электрона и авиалайнера) по эффекту Доплера – изменению частоты рассеянного назад излучения. В принципе данные о скорости можно получить по анализу всего нескольких фотонов, попавших в детектор. Конечно, эти фотоны взаимодействуют с исследуемым объектом. Понятно, однако, изменение импульса авиалайнера в результате такого взаимодействия ничтожно мало вне зависимости от частоты используемого излучения. Что касается электрона, изменение его импульса будет существенным, особенно если использовать коротковолновое излучение, позволяющее одновременно определить пространственное положение электрона с высокой точностью.
Дата добавления: 2017-01-16; просмотров: 1926;











