Идеальный газ. Основное уравнение МКТ идеального газа (уравнение Клаузиуса)

И его следствия.

Для газообразного состояния вещества характерно относительно большое расстояние между молекулами и значительное преобладание сил отталкивания над силами притяжения.

При обычных условиях молекулы газов находятся на расстояниях, значительно превышающих их собственные размеры, поэтому силы притяжения между ними и их собственный объём можно не учитывать.

Газ, конечными размерами и, взаимодействием между молекулами которого, можно пренебречь называют идеальным.

Данную модель газа можно использовать при изучении реальных газов, т.к. при нормальных условиях они ведут себя подобно идеальному.

Для описания свойств материи с точки зрения молекулярной физики используется ряд физических величин, называемых параметрами.

Величины, относящиеся к отдельно взятой молекуле, называют микропараметрами.

Как, например, скорость, импульс, энергия молекул.

Макропараметрами называют величины, присущие веществу в целом.

Одной из задач МКТ газа является установления связи между микро- и макропараметрами вещества. Уравнение, отражающее эту связь, называют основным уравнением МКТ .

Основное уравнение МКТ идеального газа ( уравнение Клаузиуса)

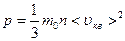, (3)

где m₀ – масса молекулы; n – концентрация; < 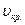> - средняя квадратичная скорость молекул:

.

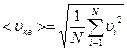Множитель 1/3 в уравнении Клаузиуса обусловлен трёхмерностью пространства.

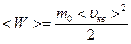Учитывая также, что - средняя кинетическая энергия молекул, полученное уравнение можно записать в виде: 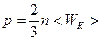. (4)

Заметим, что полученные уравнения действительно связывают макропараметр P с микропараметрами < 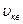.>² и <Wк>.

Полученное нами ранее уравнение Клаузиуса, является основным уравнением МКТ газа, поскольку из него вытекает ряд следствий. Рассмотрим некоторые из них.

Умножим обе части уравнения Клаузиуса на :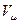

.

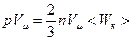Рассмотрим подробнее произведение: .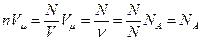

С учётом этого запишем: .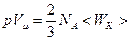

С другой стороны, из уравнения состояния для одного моля газа, имеем:

.

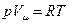Решая систему уравнений, получаем:

.

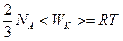Откуда следует уравнение Больцмана:

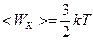, (5)

где k – коэффициент Больцмана. Из полученного уравнения следует, что температура является мерой кинетической энергии молекул газа.

Подставляя полученное выражение в уравнение Клаузиуса, получим уравнение состояния:

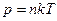. (6)