Система уравнений Максвелла.
Фундаментальные законы и основные уравнения электродинамики позволили Максвеллу, после выполнения необходимых математических операций, вывести систему общих электромагнитных уравнений для любой непрерывной, неподвижной среды, связанной жестко с Землей (при отсутствии сторонних токов и сторонних зарядов).
К ним относятся:
1. 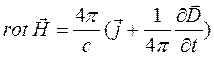 (12) – 1 уравнение Максвелла.
(12) – 1 уравнение Максвелла.
2. 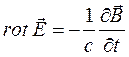 (13) – 2 уравнение Максвелла.
(13) – 2 уравнение Максвелла.
3. 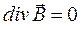 (14) – 3 уравнение Максвелла.
(14) – 3 уравнение Максвелла.
4. 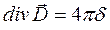 15) – 4 уравнение Максвелла.
15) – 4 уравнение Максвелла.
Приведенные уравнения Максвелла не содержат электромагнитных параметров среды и описывают универсальные свойства электромагнитного поля, объективно существующего в данной среде.
В данных формулах:
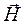 - вектор напряженности магнитного поля;
- вектор напряженности магнитного поля;
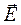 - вектор напряженности электрического поля;
- вектор напряженности электрического поля;
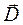 - вектор электрической индукции (электрическое смещение);
- вектор электрической индукции (электрическое смещение);
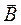 - вектор магнитной индукции;
- вектор магнитной индукции;
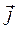 - вектор плотности токов проводимости;
- вектор плотности токов проводимости;
δ – плотность электрических зарядов.
Эта система уравнений не может быть решена однозначно, так как содержит пять неизвестных векторов 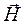 ,
, 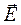 ,
, 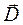 ,
, 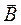 ,
, 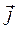 при системе из четырех уравнений.
при системе из четырех уравнений.
Для того, чтобы определить электромагнитное поле в конкретной среде, необходимо воспользоваться связями между векторами 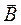 и
и 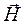 ,
, 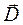 и
и 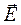 ,
, 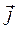 и
и 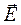 вида:
вида:
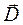 = ε
= ε 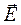 ,
, 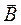 = μ
= μ 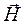 ,
, 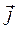 = γ
= γ 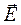 , (16)
, (16)
где γ, ε, μ есть соответственно, электропроводность, диэлектрическая проницаемость и магнитная проницаемость среды. Материальные параметры γ, ε, μ для изотропной среды являются скалярными величинами и характеризуют электромагнитные свойства среды.
В формулах связи (16) параметры γ, ε, μ могут быть постоянные величинами или в виде функций от компонент поля (при интенсивных полях), от частот (при сверхнизких и сверхвысоких частотах) и от времени (при неустановившихся процессах).
В однородно – изотропной среде увеличение значение ε уменьшает напряженность электрического поля 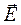 , а увеличение значения μ повышает магнитную индукцию
, а увеличение значения μ повышает магнитную индукцию 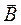 среды.
среды.
Дата добавления: 2021-05-28; просмотров: 504;











