Примеры капитальных прорезей

Наиболее распространенный вид капитальных прорезей – прорези, отторгающие нижний побочень переката. Отторжение является целесообразным, когда нижний побочень сильно развит и смещается вниз по течению медленнее верхнего. При сближении побочней судовой ход на перекате искривляется и становится неудобным для судоходства. Прорезь, расположенная почти поперек русла, быстро заносится. А русловой поток, обычно, сам уже начинает промывать спрямляющую борозду через нижний побочень. Капитальная прорезь намечается по этому направлению.

Различают два случая отторжения нижнего побочня: полное отторжение, когда капитальная прорезь проходит через корневую часть побочня, и частичное отторжение, когда прорезь прокладывается в центральной части побочня.

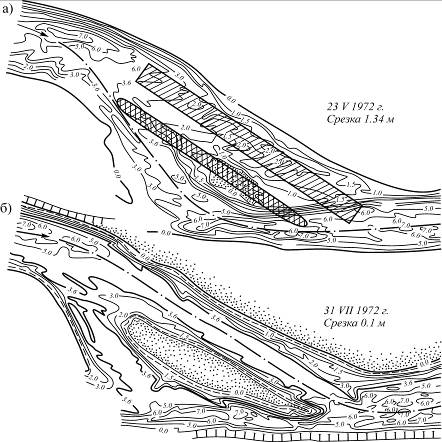
Рис. 4.9. Отторжение нижнего побочня на Верхнем Просецком перекате р. Волги:

а – съемка до работ: б – съемка после работ

Первый случай показан на рис. 4.9, здесь приведены два плана Верхнего Просецкого переката р. Волги - перед производством дноуглубительных работ и по окончании разработки капитальной прорези. Из прорези длиной 1800 м, проложенной через корневую часть обширного побочня, было извлечено около 950 тыс. м³ грунта. По контрольной съемке видно, что прорезь была поддержана потоком. И уже через два месяца начал происходить процесс занесения старого судового хода.

Второй случай отторжения показан на рис. 4.10. Здесь представлены два плана одного из перекатов р. Амур – до и после разработки капитальной прорези, которая произвела частичное отторжение нижнего побочня. Новое направление судового хода было уже подготовлено потоком, поэтому объем капитальной прорези составил лишь 90 тыс. м³ грунта при ее длине в 850 м. На контрольной съемке видно, что новый судовой ход быстро развивается, а на старом - идет процесс отложения наносов.

Развитие русловых деформаций после отторжения побочня далеко не всегда бывает таким благоприятным, как на представленных перекатах. Если емкость старого судового хода велика, она продолжает отвлекать большой расход воды, и капитальная прорезь оказывается неустойчивой. Чтобы закрепить новое положение судового хода, приходится принимать меры по уменьшению пропускной способности старого судового хода. Это может быть укладка отвала грунта на старый судовой ход или возведение специальных выправительных сооружений.

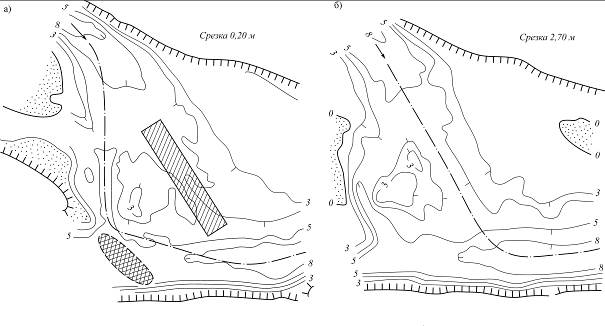
Рис. 4.10. Частичное отторжение нижнего побочня на перекате р. Амур:

а – съемка в июле 1942 г. (до работ); б – съемка в октябре 1942 г. (после работ)

Зачастую затруднения возникают, когда капитальная прорезь разработана преждевременно, т.е. поток сам еще не начал прокладывать себя путь через побочень. О достижении благоприятной стадии можно судить по появлению промоин на поверхности побочня. Если же выполнение прорези требуется по условиям судоходства, необходимо придавать ей большую ширину (до 2-3 гарантированных ширин судового хода).

Наиболее крупные капитальные прорези выполняют при переносе судового хода из одного в другой рукав разветвленного участка русла. Перенос почти всегда делается из более длинного и искривленного в более короткий и прямой рукав. Этим не только достигают улучшения условий судоходства, но и обеспечивают большую устойчивость судового хода. В коротком рукаве уклон свободной поверхности и транспортирующая способность потока больше, чем в длинном. Основанием для переноса судового хода обычно служит установленная при анализе руслового процесса тенденция к обмелению судоходного и размыву несудоходного рукава. Иногда прямой и короткий рукав не развивается из-за того, что в нем залегают гравелистые или глинистые грунты, хорошо сопротивляющиеся размыву. Выполнив в таком рукаве капитальную прорезь с помощью многочерпаковых снарядов, можно получить удобный и очень устойчивый судовой ход.

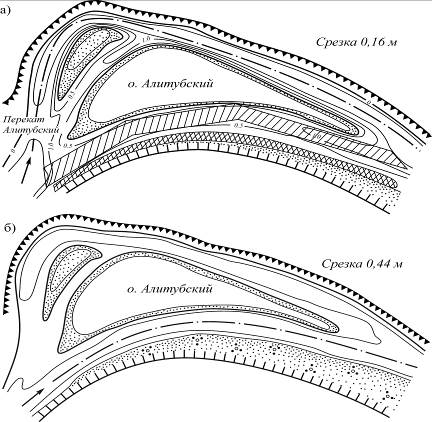
Рис. 4.11. Перенос судового хода из левого

в правый рукав Алитубского разветвления р. Дона:

а – съемка в июне 1953 г. (до работ); б – съемка в июне 1960 г.

(после стабилизации нового судового хода)

На рис. 4.11,а показана капитальная дноуглубительная прорезь на Алитубском разветвлении р. Дон. Правый рукав разветвления, более короткий и широкий, чем левый, долгое время оставался несудоходным из-за малых глубин. Дно этого рукава слагали крупнозернистые пески, и скорость течения в нем была меньше неразмывающей.

Перенос судового хода в правый рукав был обусловлен большой кривизной левого рукава и существованием на входе в него Алитубского переката, на котором ежегодно выполнялись дноуглубительные работы. При разработке правого рукава было извлечено около 900 тыс. м³ грунта. В течение шести лет на новом судовом ходу велись ремонтные дноуглубительные работы, а левый рукав постепенно мелел. К 1960 г. ход в правом рукаве стабилизировался и перестал требовать дноуглубления (см. рис. 4.11, б).

Поддержание судоходных условий на реках, протекающих в северных районах, обладает определенной спецификой, связанной с сезонной промерзаемостью мелководных рукавов и русловых форм. Комплексные исследования северных рек в районах газонефтедобычи в течение длительного времени (с 1975 г.) проводились Западно-Сибирской экспедицией ЛИВТа. В качестве примера на рис. 4.12 показан план участка реки Пур, впадающей в Тазовскую губу. Материалы, полученные экспедицией в 1981 г., охватывают бытовое состояние этого участка. Они включают в себя план участка исследований, результаты обработки материалов гидрометрических измерений и продольные профили свободной поверхности воды на участке.

На этой основе был составлен проект коренного улучшения судоходных условий на участке, предусматривающий разработку капитальной дноуглубительной прорези в левом рукаве. Прорезь была затрассирована с двумя изломами по направлению стрежня меженного потока.

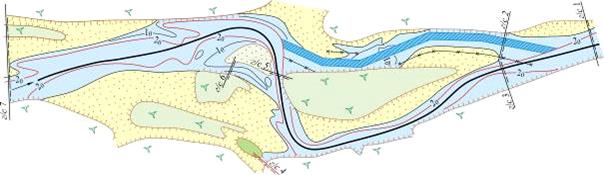
Рис. 4.12. Схема исследуемого участка р. Пур:

– капитальная дноуглубительная прорезь;

– местоположение отвалов грунта;

– расположение гидрометрических створов

В подготовительный период навигации 1982 года в соответствии с проектом на участке были выполнены дноуглубительные работы объемом около 500 тыс. м³. Разработка прорези осуществлялась двумя землесосами производительностью 1000 м³/ч. После разработки капитальной прорези произошло перераспределение расхода воды в пользу левого рукава, что позволило перенести судовой ход в этот рукав и обеспечивать в нем судоходство в дальнейшем без значительных объемов ремонтных работ.

Натурные исследования, выполненные на этом участке в бытовом состоянии и после производства дноуглубительных работ, позволили оценить эффект влияния капитальной дноуглубительной прорези на гидравлику разветвленного участка реки. Это позволило получить новые научные данные для повышения надежности гидравлических расчетов [3].

Во всех рассмотренных примерах коренное улучшение судового хода на перекатах достигалось с помощью капитальной прорези и отвала грунта, т.е. только средствами дноуглубления. Нередко, капитальные прорези выполняют в комплексе с возведением выправительных сооружений. При этом удается улучшать протяженные участки русла, включающие в себя несколько затруднительных перекатов.

4.7. Построение планов течения

Общие сведения. Основой для прогноза деформаций прорези является поле скоростей течения. Построить такое поле с учетом запроектированной (еще не существующей) прорези и отвала можно путем расчета или с помощью гидравлического и аэродинамического моделирования. К моделированию прибегают для отдельных наиболее сложных участков русла, где проектируется комплекс дноуглубительных и выправительных работ. Исследования ведут на открытых гидравлических или на напорных аэродинамических моделях. Принципиальные основы моделирования излагаются в курсе гидравлики. Ниже рассматриваются только расчетные методы построения скоростных полей.

Зависимости, определяющие расход наносов, связывают его со средней скоростью течения на вертикали, поэтому построение скоростных полей ведется в этом же приближении: искомой служит плановая (двумерная) картина течения, составленная векторами средних скоростей на вертикали. Движение потока считается установившимся. Векторными линиями поля скоростей являются линии тока. Плановой линией тока будем называть линию в горизонтальной плоскости, направление касательной к которой во всех ее точках совпадает с направлением вектора средней скорости на вертикали (отклонениями этих векторов от горизонта можно пренебрегать). Линии, ортогональные к плановым линиям тока, представляют собой горизонтальные проекции живых сечений. Эти линии называют криволинейными поперечниками. Совокупность плановых линий тока и криволинейных поперечников называется планом течения (рис. 4.13).

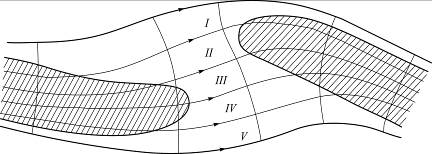
Рис. 4.13. План течений (I-V номера струй)

Часть потока, заключенная между двумя смежными линиями тока, называется плановой струей. Полоса между двумя смежными криволинейными поперечниками называется поясом плана течений.

При неплавно изменяющемся движении воды, которое часто наблюдается на перекатах, построение плана течений основывается на решении двумерных уравнений установившегося неравномерного движения открытого потока. В эти уравнения входят силы тяжести и трения, а также силы инерции, обусловленные конвективными ускорениями воды. Такое решение можно получить только численными методами.

Исторически первым был алгоритм ручного счета, предложенный еще в тридцатых годах Н.М. Вернадским.

В 80-е годы прошлого столетия появились алгоритмы машинного счета, среди которых следует отметить метод И.А. Шеренкова. Одним из его преимуществ является возможность применения ЭВМ с небольшим объемом памяти. Наличие в методе Шеренкова некоторых упрощений обязывает, однако, к продолжению работ над алгоритмами численного решения плановой задачи движения речного потока. В последние годы, в связи с активным развитием средств вычислительной техники, все большее применение на практике находят численные методы решения уравнений гидравлики, основанные на использовании метода конечных элементов. Наиболее эффективные алгоритмы и программы, применимые для решения задач речной гидравлики, были разработаны в Вычислительном центре РАН авторами А.Н. Милитеевым и В.В. Беликовым.

Расчет планов течений при плавно изменяющемся движении не такой сложный. В этом случае кривизна и расходимость плановых линий тока незначительны, а силы инерции могут быть отброшены и криволинейные поперечники заменены прямыми. Такой метод расчета был предложен М.А. Великановым и получил название метода плоских сечений. Некоторые простые задачи неплавно изменяющегося движения могут быть решены посредством модифицированного метода плоских сечений, известного под названием метода фрагментов (предложен К. В. Гришаниным).

Таким образом, в распоряжении инженера-путейца в настоящее время есть несколько способов построения планов течений. Рекомендуемые области их применения следующие. Построение планов течений на относительно простых перекатах, расположенных на прямолинейных или слабо изогнутых участках русел и не имеющих затонских частей, следует вести по методу плоских сечений. На перекатах с затонской частью следует применять ме­тод фрагментов. Для сильно искривленных участков русел с неплавно изменяющимся движением воды необходимо выполнять решение полных уравнений планового движения по методу Шеренкова или с использованием современных численных методов вычислений.

Ниже излагаются основы двух первых методов. С методом Шеренкова можно ознакомиться по его монографии [4].

Метод плоских сечений. При плавно изменяющемся движении потока уклон свободной поверхности вдоль произвольной плановой линии тока можно выразить с помощью формул Шези и Маннинга

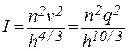, (4.7)

где: n – коэффициент шероховатости;

h – глубина вертикали;

v – средняя скорость на вертикали;

q – элементарный расход воды.

Решая его относительно элементарного расхода, получим

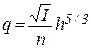. (4.8)

Уравнение неразрывности записывается в интегральной форме так

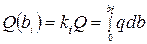, (4.9)

где: Q (b_i) – расход воды, проходящий в полосе между урезом, принятым за начало отсчета поперечных расстояний, и i-й линией тока.

Стремясь сделать выбор линий тока определенным, вводят условие, чтобы между любой парой смежных линий тока проходил один и тот же расход воды. Это значит, что речной поток делится на целое число N равнорасходных плановых струй. Отношение 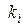при этом записывается в виде .

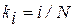Подставив величину элементарного расхода по уравнению (4.8) в уравнение неразрывности (4.9), будем иметь

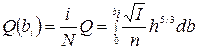. (4.10)

На участках с плавно изменяющимся движением допустимо считать, что продольный уклон не изменяется поперек русла. Такое же допущение можно принять и в отношении коэффициента шероховатости

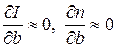. (4.11)

Это позволяет вынести множитель 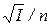из-под знака интеграла в уравнении (4.10)

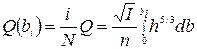. (4.12)

Таким образом, в методе плоских сечений распределение расхода по ширине русла зависит только от глубин.

Уравнение (4.12) является расчетным. Неизвестной в нем служит координата b_i. Значения координаты b_i, определяющие границы равнорасходных струй, легко найти в каждом поперечном сечении графическим способом (рис. 4.14). Построив поперечный профиль русла и отвечающий ему график подынтегральной функции h^5/3 =f(b), проводят графическое интегрирование и строят на том же чертеже интегральную кривую

.

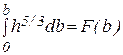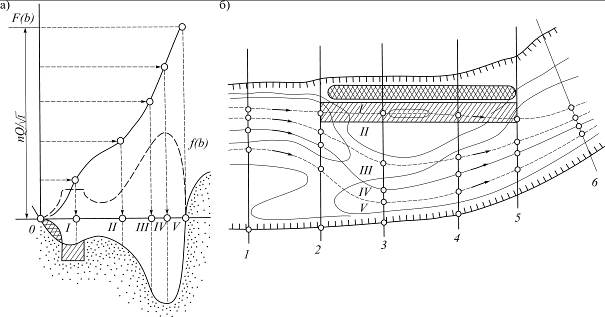
Рис. 4.14. Построение плана течений на перекате

с капитальной прорезью по способу плоских сечений:

а – расчет распределения расхода по ширине одного из поперечников;

б – построение границ равнорасходных струй; I – V - номера плановых струй

Конечная ордината интегральной кривой равна 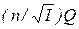, т.е. пропорциональна полному расходу. Разделив ее на N равных частей, сносят точки деления на интегральную кривую, а затем на ось b, как показано на рис. 4.14, а. Это и есть границы равнорасходных струй в поперечном сечении. После выполнения расчетов для всех сечений границы струй переносят на план переката и соединяют плавными линиями (рис. 4.14, б). Число N плановых струй берется обычно 3-5.

Расчетные поперечники назначаются в глубоких местах плесовых лощин, на гребнях, на переходах от плесовых лощин к перекатам и от перекатов к плесовым лощинам. Расстояние между сечениями должно быть соизмеримо с шириной русла. Через намеченную прорезь необходимо назначить не менее 4-5 поперечников, крайние из которых, должны проходить через начало и конец прорези. Если расчет проводится для больших наполнений русла, поперечники располагаются по нормалям к оси русла. При расчете для малых наполнений на направление течения сильное влияние оказывает рельеф дна и поперечники следует ориентировать, сообразуясь с этим рельефом так, чтобы они были нормальны к предполагаемому направлению течения.

Метод фрагментов. На участках, где условия плавно изменяющегося движения не соблюдаются, уклон свободной поверхности может изменяться по ширине русла. Для этих случаев К.В. Гришанин предложил разбить поток в плане на фрагменты, в пределах каждого из которых поперечным изменением уклона допустимо пренебречь. Тогда в пределах каждого фрагмента можно применять метод плоских сечений, но предварительно необходимо найти распределение расхода воды между фрагментами.

Простейший пример использования этой идеи дает построение плана течений на разветвленном участке русла. Пусть река делится на два рукава. Уклоны свободной поверхности в рукавах могут сильно различаться. Поэтому сначала следует рассчитать распределение расхода между рукавами, а затем строить планы течений отдельно для каждого рукава.

Метод фрагментов позволяет успешно решить задачу построения плана течений для перекатов с затонской частью, где гипотеза однозначного соответствия между глубинами и элементарными расходами при низких уровнях не выполняется. При малых наполнениях русла, уклоны свободной поверхности в затонской части меньше уклонов в верхней плесовой лощине и, распределяя расходы пропорционально значениям h^5/3, можно сильно завысить расход, пропускаемый затонской частью.

Деление на фрагменты непосредственно вытекает из общей картины течения: к одному фрагменту относятся верхняя плесовая лощина и напорный скат переката, к другому – затонская часть вместе с тыловым скатом. Граница между фрагментами проходит по гребню перекатного вала (рис. 4.15). Перелив воды через косой перекатный вал приводит к тому, что расход в верхней плесовой лощине вниз по течению убывает, а по затонской части нарастает. Изменение расходов воды по длине фрагментов существенно осложняет задачу распределения расхода между фрагментами.

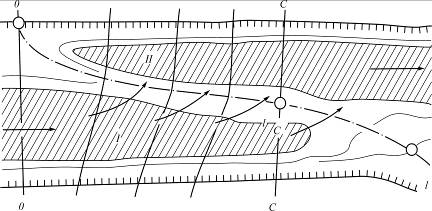
Рис. 4.15. Фрагменты плана течений на перекате с затонской части

Отсчитывая продольные расстояния по криволинейной границе между фрагментами, можем написать следующие условия неразрывности:

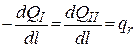(4.13)

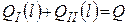(4.14)

Индексами I и II обозначены, соответственно, расходы воды в верхней плесовой лощине и в затонской части, a q_r = q_r (l) - удельный расход на гребне перекатного вала. Задача о распределении расхода между фрагментами будет решена, если мы будем знать одну из функций Q_I(l) или Q_II(l) так как другая функция найдется из уравнения (4.14). Интегрируя второе из равенств (4.13), получим

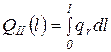. (4.15)

Вал переката работает при низких уровнях как косой затопленный водослив и, принимая приближенно, что разность отметок свободной поверхности в верхней плесовой лощине и в затонской части сосредоточена над гребнем этого водослива, можем написать следующее выражение для удельного расхода на гребне

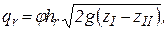(4.16)

где: φ – коэффициент скорости;

h_r = h_r (l) – глубина на гребне;

Z_I, Z_II – соответственно отметки свободной поверхности в верхней плесовой лощине и в затонской части.

За исключением прибрежных частей перекатного вала перепад уровней на его гребне изменяется мало. В соответствии с соотношением (4.16) это значит, что удельный расход на гребне можно считать пропорциональным глубине h_r. Тогда вместо уравнения (4.15) будем иметь следующее условие пропорциональности

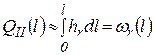, (4.17)

где: функция ω_r(l) выражает нарастание площади сечения вдоль гребня переката по линии l.

Вблизи корыта перекатного вала различие между уклонами свободной поверхности в верхней плесовой лощине и в затонской части сглаживается. Поэтому в проведенном здесь поперечном сечении (сечение С-С на рис. 4.14) расход можно распределить от одного берега до другого пропорционально значениям h^5/3. Это значит, что мы легко можем установить здесь долю расхода, пропускаемую затонской частью Q_II(l_c) = Q_IIc. Используя соотношение (4.17), получаем формулу для расчета расхода воды вдоль затонской части переката

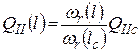, (4.18)

где: 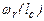– часть живого сечения на гребне переката, ограниченная координатами l=0 и l=l_c (рис. 4.16).

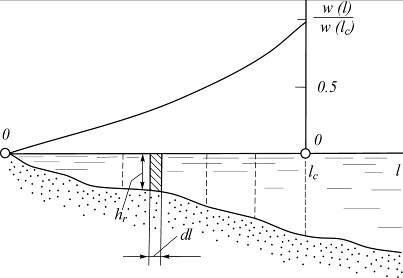
Рис. 4.16. Профиль живого сечения на гребне переката с затонской частью

и график нарастания площади сечения вдоль гребня

Расчеты при построении плана течений на перекате с затонской частью выполняют в следующем порядке.

1. Делают разбивку расчетных (ломаных) поперечников, начиная с входного сечения 0-0. Проводят линию 0l по гребню переката (см. рис. 4.15). В отношении разбивки поперечников сохраняют силу указания, сделанные для метода плоских сечений.

2. Строят сечение русла по линии гребня от точки l = 0 до точки l = l_c, определяют для ряда значений l площади ω_r и строят безразмерный график нарастания этих площадей (см. рис. 4.16)

.

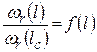3. Вычерчивают конечное поперечное сечение С-С и строят для него интегральную кривую

.

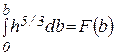4. С помощью интегральной кривой по измеренному на плане переката расстоянию b_IIc от уреза затонской части до гребня переката устанавливают расход воды Q_IIc в конечном сечении затонской части.

5. По формуле (4.18) определяют значения расхода Q_II во всех расчетных сечениях затонской части и затем по формуле (4.14) – значения расхода Q_I в расчетных сечениях верхней плесовой лощины.

6. Задают число N плановых струй и находят расход одной струи Q/N.

7. Вычерчивают все расчетные поперечники и строят для двух фрагментов отдельные интегральные кривые F(b). С помощью интегральных кривых по отношениям Q/NQ_II и Q/NQ_I находят границы плановых струй в расчетных сечениях. Полученные точки переносят на план переката и соединяют плавными линиями.

При большом объеме расчетов целесообразно пользоваться вычислительными машинами. В.М. Селезнев разработал алгоритмы и программы счета на ЭВМ для обоих применяющихся в проектировании прорезей методов построения планов течений – метода плоских сечений и методов фрагментов.