Обучение математике в школах XIII-XVI вв. Первые учебные пособия.

В XIII- начале XIV века основными центрами культуры были, по-прежнему, монастыри и церкви. Именно при монастырях собирались библиотеки рукописей, образовывались школы, в которых детей учили чтению, письму, пению и счёту. Содержание математического образования было минимально: первоначальные сведения о нумерации, сложение и вычитание именованных чисел, некоторые сведения о простых дробях.

В XV веке стали появляться конфессиональные школы (по вере) (≈ среднее и высшее образование). В 1639 г. на базе слияния 2 школ появилась Киево-Могилянская коллегия (прототип ВУЗа), впоследствии в 1701 г. получившая звание академии. Она состояла из 6 классов (5 – одногодичные и шестой – 2 года), в 1-5 классах изучали грамматику, синтаксис, поэтику и языки (славянский, греческий, латинский, польский), в 6 классе изучали философию, в состав которой входили арифметика и геометрия). Киево-Могилянская академия сыграла большую роль в развитии культуры не только для Украины, но и для всей России, она была крупнейшим образовательным центром, дала таких деятелей в области просвещения, как Епифаний Славинецкий (ок. 1600-1675, иеромонах, переводчик греческих трудов) и Симеон Полоцкий (1629 - 1680), деятель восточнославянской культуры, духовный писатель, богослов, поэт, драматург, переводчик). Позднее в 1661 г. открыта вторая академия – Львовская. По образцу Киево-Могилянской коллегии в 1687 г. в Москве была организована Славяно-греко-латинская академия. Т.к. Украина и Белоруссия были в то время под властью Польши, то на их территории создавалось множество иезуитских школ. В противовес им возникали братские школы (XVI-XVII вв.)для коренного населения, основная задача которых – сохранение национальной культуры (Львов (1586), Перемышль, Киев, Луцк, Вильно и др.).

Авторы первых учебных пособий XVI века различали 2 вида арифметики: линейную и численную.

Линейная арифметика (арифметика на линиях). На линиях выполнялись действия над целыми числами (нумерация, сложение, вычитание, умножение и деление), основанные на тех же принципах, что и индийская нумерация. Число изображалось на линиях счётной доски почти так, как на счётах. Отличие в том, что числа могли быть и между линиями, тогда каждый камушек обозначал 5 единиц разряда нижней линии.

Числовая арифметика (цифровая). Учебники в разделе «нумерация» учили записывать числа с помощью 10 знаков, для действий давали определения. Изложение сложения и вычитания сложностей не вызывало. Изложение умножения начиналось с таблицы умножения, затем – правило умножения на числа, меньшие 5 – правило лентяя (на пальцах), способ умножения в клеточкахи другие способы.

Правило умножения однозначного числа на 9. Например, n×9. Поднять n-ый палец, слева – число десятков, справа – единиц.

Правило «решетки» (в клеточках»). 568×7=?

1. Чертим решетку с тремя столбцами и одной строкой, разделяем ячейки решетки на две части по диагонали.

2. Умножаем старший разряд множимого на множитель (5*7 = 35) и записываем результат в первую ячейку, причем разряд десяток записываем в верхнюю часть ячейки, а разряд единиц - в нижнюю.

3. Умножаем разряд десятков множимого на множитель (6*7 = 42) и записываем результат во вторую ячейку.

4. Умножаем разряд единиц множимого на множитель (8*7 = 56) и записываем результат в третью ячейку.

5. Суммируем строку решетки по наклонной плоскости справа налево. Суммирование по наклонной плоскости проводится поразрядно с переносом переполнения в старший разряд. Каждый разряд равен сумме чисел в прилегающих друг к другу треугольниках соседних ячеек. Полученная сумма - это результат умножения.

При делении на однозначное число, если оно не больше первой цифры делимого, то его записывали под ней, если больше – то под второй цифрой делимого. Аналогично поступали и при делении на многозначное число. Само деление выполнялось по алгоритму Евклида, но записи при делении производились различными способами. Например, 942 : 42 = ?

942 2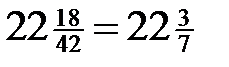

42 Все арифметические действия проверялись или правилом девятки, или

2 обратным действием, законы действий не формулировались, а предлагались

84 в виде советов, общепринятой терминологии не было.

102 Большинство учебников рассматривали прогрессии как арифметическое

42 22 действие и делили прогрессии на натуральные (непрерывные) и разрывные.

2 Например, натуральная: 1, 2, 3, 4,…, разрывная: 1, 3, 5, 7, ... или 2, 4, 6, 8, …

84 Кроме того, имелись правила вычисления суммы членов для случаев, когда

18 последний член прогрессии четен (нечетен).

В арифметику включалось извлечение корней (2 и 3 степени) по формулам для квадрата суммы и куба суммы, но запись была иной.

Особый раздел представляли действия с дробями (+, -, ×, :) , а также удвоение дроби и деление пополам, причём запись не отличалась от современной. Перед разделом обычно помещались сведения о преобразованиях дробей (сокращение, нахождение НОД по алгоритму Евклида, сравнение дробей, приведение их к общему знаменателю = произведению их знаменателей).

Ещё один раздел был посвящён правиламдля решенияарифметических задач(обычно это тройное правило и правило фальшивого положения). Тройное правило состояло из простого (прямая и обратная зависимость, правило для целых и для дробей) и сложного (дважды применённое простое). Простое тройное правило записывалось в виде схемы, с помощью которой по трём известным величинам находили четвёртую (неизвестную) величину. Оно являлось основой правил «товарищества», «смесей», «убытка и прибыли», «разностей» и применялось для решения различных типов задач.

Много внимания в русских учебниках уделялось правилу фальшивого положения, представлявшему алгоритм для решения линейного уравнения первой степени и применявшемуся для решения практических задач.

Пусть нужно решить уравнение а·х+в=0. Выбираем произвольные х₁ и х₂ и вычисляем: у₁=а·х₁+в, у₂=а·х₂+в. Легко проверить, что искомое значение х будет равно х=(х₂·у₁-х₁·у₂)/(у₁-у₂).

Итак, в XVI-XVII в. арифметику изучали с помощью счёта на линиях (преимущественно в XVI в.) и индусской нумерации, причём изложение носило догматический характер, правила давались без выводов в виде «рецептов», но с примерами. Часто использовалась 5 книга «Начал» Евклида.

Известными учебными пособиями по геометрии были «Геометрия или Измерительная наука» С. Гжепского и «Обучение математике» (1630) Я. Стегмана.

Станислав Гжепский(1523-1570) - польский землемер, математик, учитель – положил в основу своего учебника, представляющего практический курс, «Начала» Евклида. В нём даны не только формулировки, но и доказательства теорем.

Я. Стегман - ректор школы Польских братьев в Ракуве (1603-1638), польский просветитель, математик. Его учебник тоже содержит сведения по практической геометрии, которую автор определял как «часть математики о величинах». Содержанием геометрии, по его мнению, является изучение непрерывных величин, важнейшими из которых он считал линию, плоскость и телои определял их двояко: с помощью движения и таким образом: точка – граница линии, линия – граница поверхности, поверхность – граница тела. В учебнике:

· мера отрезка определена как отношение отрезка к единице длины; измеряются отрезки с помощью циркуля и линейки;

· решены простейшие задачи на построение, но без объяснений, некоторые – несколькими способами, включающими построения на местности (деление отрезка пополам, на несколько частей, проведение перпендикуляра к прямой в данной точке и из точки, лежащей вне прямой, построение прямой, параллельной данной, построение угла, равного данному и деление угла пополам);

· линии делятся на кривые и прямые (встречные, параллельные, секущие, перпендикулярные, касательные);

· определены понятия (периметр, радиус, центр и диаметр) для многоугольника (не для окружности), подобных и равных фигур;

· площади квадрата, прямоугольника и параллелограмма вычисляются разбиением их на треугольники без объяснений;

· треугольник – фигура с тремя углами и тремя сторонами; в треугольниках с равными углами соответствующие стороны пропорциональны – это положение считается очень важным для геодезии и геометрии;

· рассмотрены задачи о преобразованиях прямоугольников в равновеликие треугольники;

· изложены классические задачи по измерению на местности;

· площадь треугольника вычисляется 2 способами: по формуле Герона и ;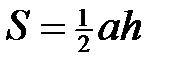

· дано понятие четырёхугольника, выделены его виды (параллелограмм и трапеция), рассмотрены некоторые их свойства, помещены решения 10 задач (на построение фигур, равновеликих данным: = ; = ; = . В большинстве решений нет построений, только описания;

· в разделе «О многоугольниках» рассмотрено построение многоугольников и вычисление их углов;

· круг определён как круглая фигура, эллипс – как удлинённая фигура, но площадь круга и сектора вычислены правильно; площадь эллипса вычислена «разделением его на 2 полукруга и параллелограмм»;

· изложен материал по стереометрии; поверхности разделены на цилиндрические, конические и сферические и определены как поверхности вращения, а правила вычисления их площадей соответствуют современным формулам;

· правильно классифицированы многогранники и вычислены их объёмы (кроме объёма бочки);

· помещены некоторые сведения по тригонометрии, но их мало.

Итак, курс геометрии преподавался на уровне сообщения практических знаний, как и всюду в Западной Европе того периода.

3) Математика в России XII века