Обработка наблюдений за расходами воды
Расходы воды в реках, постоянно изменяющиеся в течение года (рис. 20) и по годам, используют для определения расчетных модулей стока по фактическим наблюдениям, вычисления величины твердого стока, планирования водохозяйственных мероприятий.
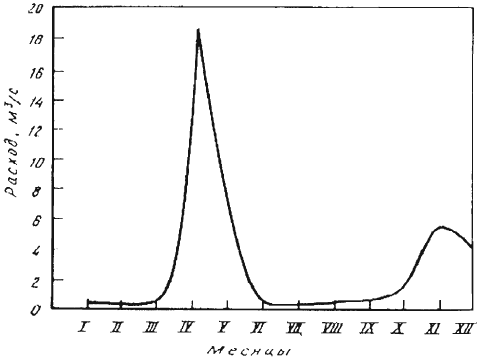
Рис. 20. Гидрограф стока р. Тосно (1980 г.)
Построение кривой обеспеченности расходов. При проектировании осушительных систем для определения размеров проводящих каналов, расчета диаметров труб, ширины отверстий водосбросных сооружений, пролетов мостов и других целей вследствие большой изменчивости расходов необходимо знать их обеспеченность (вероятность превышения). Обеспеченность определенного значения расхода, модуля или уровня показывает вероятность появления и превышения данных величин и вычисляется в процентах (от 100 %). Например, с вероятностью 100 % можно утверждать, что в непересыхающих водотоках будет постоянно наблюдаться движение воды, но с очень малой вероятностью возможен катастрофически большой расход (или уровень). Обеспеченность наглядно характеризуется теоретической кривой обеспеченности (рис. 21).
Вследствие большой изменчивости расходов для построения кривой обеспеченности необходимо иметь достаточно продолжительный ряд наблюдений. Вполне достоверный результат можно получить при использовании только длительных, не менее 30-50 лет, наблюдений. Однако в практике гидрологических расчетов, особенно при проектировании осушения лесных земель в удаленных районах, не всегда есть возможность вести длительные наблюдения, приходится ограничиваться краткими 15-20-летними наблюдениями.
Построению кривой обеспеченности предшествует обработка результатов наблюдений. В таблице 8 приведена обработка 15-летних наблюдений за расходами воды в р. Тигода. В основу обработки положены методы математической статистики.
Таблица 8 - Вычисление параметров кривой обеспеченности средних годовых расходов (р. Тигода; F = 58900 га)
| № и/п | Год | Расход, м3/c | К | К - 1 | (К – 1)2 | Обеспеченность, % |
| 6,00 | 1,57 | 0,57 | 0,324 | 4,5 | ||
| 4,88 | 1,28 | 0,28 | 0,078 | 11,0 | ||
| 4,84 | 1,27 | 0,27 | 0,073 | 17,5 | ||
| 4,82 | 1,26 | 0,26 | 0,068 | 24,0 | ||
| 4,62 | 1,21 | 0,21 | 0,044 | 30,5 | ||
| 4,31 | 1,13 | 0,13 | 0,017 | 37,0 | ||
| 4,13 | 1,08 | 0,08 | 0,006 | 43,5 | ||
| 4,07 | 1,07 | 0,07 | 0,005 | 50,0 | ||
| 3,52 | 0,92 | -0,08 | 0,006 | 56,5 | ||
| 3,47 | 0,91 | -0,09 | 0,008 | 63,0 | ||
| 3,33 | 0,87 | -0,13 | 0,017 | 69,5 | ||
| 2,89 | 0,76 | -0,24 | 0,058 | 75,8 | ||
| 2,48 | 0,65 | -0,35 | 0,122 | 82,5 | ||
| 2,44 | 0,64 | -0,36 | 0,130 | 89,0 | ||
| 1,39 | 0,36 | -0,64 | 0,409 | 95,4 |
По расходам разных лет Q по мере убывания их величины (графа 3) определяем среднеарифметическую величину расхода Q (среднее значение):
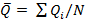 (66)
(66)
Зная среднее значение расхода, вычисляем модульный коэффициент (графа 4), который определяется отношением величины расхода каждого из членов ряда наблюдений Q к среднему значению:
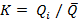 (67)
(67)
Проведя вычисления (графы 5 и 6), находим коэффициент вариации по формуле
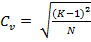 (68)
(68)
где К - модульный коэффициент; N - число лет наблюдений. В нашем примере
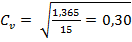
Кривая обеспеченности обычно асимметрична относительно среднего значения, ее характеризует коэффициент асимметрии СS. При небольших коэффициентах вариации коэффициент асимметрии принимается равным удвоенному коэффициенту вариации:
СS = 2 СV (69)
Коэффициент асимметрии, вычисленный по формуле (69), для данных табл. 8 оказывается равным 0,60.
Поданным табл. 8 можно вычислить эмпирическую обеспеченность каждого члена ряда по формуле Н.Н.Чегодаева:
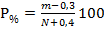 (70)
(70)
где m - порядковый номер члена ряда в ранжированном ряду; N - общее число членов ряда.
Вычисления обеспеченности членов ряда приведены в графе 7 табл. 8.
Для построения теоретической кривой обеспеченности ведут вычисления по форме табл. 9. Ординаты кривой обеспеченности вычисляют по формуле
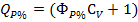 (71)
(71)
где 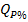 - расход воды данной обеспеченности;
- расход воды данной обеспеченности; 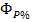 - отклонения ординат кривой Пирсона III типа от середины для соответствующего коэффициента асимметрии Сs - (принимается по таблице прил. 3); Cv - коэффициент вариации; Q - средний расход.
- отклонения ординат кривой Пирсона III типа от середины для соответствующего коэффициента асимметрии Сs - (принимается по таблице прил. 3); Cv - коэффициент вариации; Q - средний расход.
В табл. 9 приведено вычисление обеспеченности среднегодовых расходов р.Тигода. Площадь водосбора реки 58 900 га. С учетом коэффициента асимметрии по таблице прил. 3 находят отклонения ординат Ф, вводят поправку с учетом коэффициента вариации и по формуле (71) вычисляют расход воды для соответствующей обеспеченности.
Таблица 9 - Вычисление обеспеченности среднегодовых расходов (р.Тигода, СV = 0,30, СS = 0,60)
| Расчетные величины | Обеспеченность, % | |||||||||
| 0.97 | ||||||||||
| Ф | 2,75 | 2,12 | 1,80 | 1,33 | 0,61 | -0,10 | -0,72 | -1,20 | -1,45 | -1,61 |
| ФCV | 0,82 | 0,71 | 0,54 | 0,44 | 0,18 | 0,03 | 0,22 | 0,36 | -0,43 | -0,48 |
| ФCV + 1 | 1,82 | 1.71 | 1,54 | 1,44 | 1,18 | 0,97 | 0,78 | 0,64 | 0,57 | 0,52 |
| (ФCV + l) Mo=Qo% | 6,93 | 6,51 | 5,82 | 5,48 | 4,50 | 3,70 | 2,97 | 2,44 | 2,17 | 1,98 |
По данным табл. 9 строят теоретическую кривую обеспеченности (рис. 21). Для построения кривой по оси ординат откладывают расходы (м3/с), по оси абсцисс - обеспеченность Р%. Для сравнения данных на этом же графике по табл. 8 откладывают расходы (графа 3) соответствующей обеспеченности (графа 7).
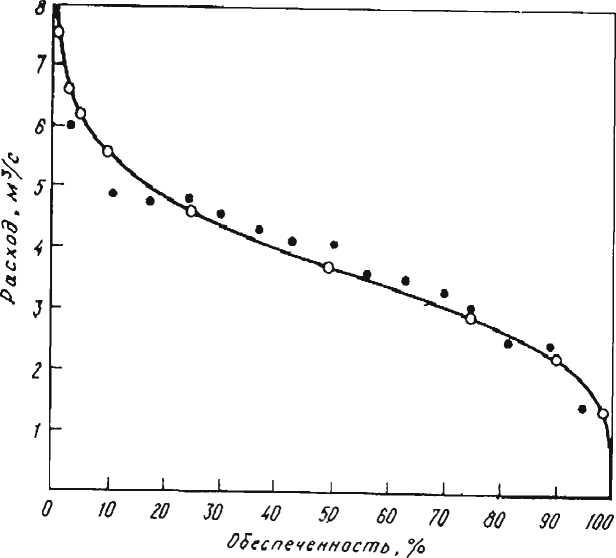
Рис. 21. Теоретическая кривая обеспеченности:
* эмпирические данные; ° расчетные значения
Построенная таким образом теоретическая кривая обеспеченности сглаживает эмпирические данные и позволяет определять величины для малых и больших значений обеспеченности за пределами экспериментального ряда.
Твердый сток
Стекающая по земной поверхности вода разрушает ее. Различают два вида деятельности поверхностных вод: смывание и размывание. При движении в руслах вода вызывает разрушение (размыв) берегов. Продукты смыва и размыва попадают в реки, образуя наносы. Наносы имеют большое экологическое влияние и промышленное значение. Они изменяют профиль дна и глубину рек в разных местах, влияют на жизнь водоемов и на рыбное хозяйство, воздействуют на работу гидроэлектростанций, на формирование дельты и пр.
Наносы могут быть взвешенными и влекомыми. Взвешенные наносы переносятся водой во взвешенном состоянии, влекомые - перемещаются по дну без подъема и в основном служат материалом для формирования отложений в руслах.
Твердый сток в основном определяется величиной взвешенных наносов. Степень насыщенности воды наносами (твердыми частицами) называют мутностью воды. Мутность измеряется весом наносов в определенном объеме воды (г/м3, мг/л). В реках России мутность изменяется от нескольких граммов до десятков килограммов в 1 м3 воды. Средняя мутность р. Невы - 5 г/м3, р. Аму-Дарьи - 2,4 кг/м3, рек Кавказа - 10-15 кг/м3. Мутность рек в течение года изменяется, наименьшая мутность наблюдается в зимнее время, наибольшая - в период половодий и паводков, а в горах - в период интенсивного таяния ледников.
Приборы, с помощью которых определяют мутность воды, называют батометрами, имеют форму бутылок различного типа (можно использовать и обычные бутылки). Поскольку мутность воды различна по глубине и ширине реки, то пробы нужно отбирать в различных точках живого сечения потока.
Вычисление стока взвешенных наносов производится по мутности воды и расходам. Среднесуточные расходы определяют по формуле:
Rср = 0,001рQ (72)
где Rcp - среднесуточный расход взвешенных наносов; р - средняя мутность воды за сутки, г/м3; Q - среднесуточный расход воды, м3/с.
Если мутность воды определяли в течение года (или периода года), то, имея данные по расходам воды (гидрограф стока, рис. 20), можно узнать общий расход твердого стока за год или любой период года.
Контрольные вопросы. 1. Что такое гидрологический режим рек? 2. Фазы водного режима рек. 5. Как устроены свайные и реечные водомерные посты? 4. Можно ли и каким образом обеспечить постоянную регистрацию уровней воды в реках, каналах? 5. Какие графики характеризуют режим уровней воды в реках? 6. Как определяется скорость движения воды в реках? 7. Как определить расход воды в реке? 8. Что такое обеспеченность? 9. Для чего необходима теоретическая кривая обеспеченности? 10. Что такое твердый сток?
Лекция 4
Дата добавления: 2021-05-28; просмотров: 899;











