Понятие о средних геометрических расстояниях

Собственная индуктивность контура (или провода) может быть определена с помощью принципа средних геометрических расстояний, если известно выра­жение взаимной индуктивности двух соответствующих экви­дистантных нитей, т. е. нитей, имеющих такую же форму и размеры, как ось рассматриваемого контура, и расположенных в параллельных плоскостях так, что соответствующие точки обеих нитей лежат на одном перпендикуляре к плоскостям и, следовательно, находятся на одинаковом рас­стоянии друг от друга (рис. 4.4) [21].

Принцип средних геомет­рических расстояний применительно к расчету собственных индуктивностей может быть сформулирован следующим образом: собственная индуктивность плоского контура из провода посто- янного сечения при равномерном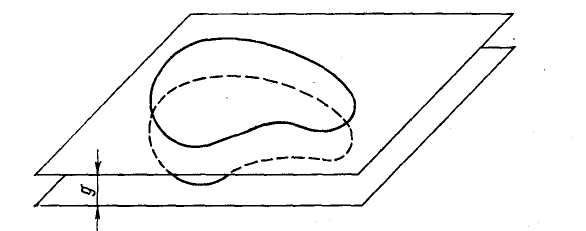
Рис. 4.4. К понятию с. г. р.
распреде­лении тока по сечению равна взаимной индуктивности соот­ветствующих эквидистантных нитей, отстоящих одна от другой на расстоянии, равном среднему геометрическому расстоянию площади поперечного сечения провода от самой себя.

Сформулированный таким образом принцип приводит к точному результату для системы, состоящей из двух беско­нечно длинных прямолинейных параллельных проводов произвольного, но постоянного сечения. Применение прин­ципа к контурам иной формы приводит к ошибке, которая, вообще говоря, тем меньше, чем меньше линейные размеры поперечного сечения провода по сравнению с размерами самого контура. Степень точности, получаемая при применении этого принципа к линейным проводам и катуш­кам, достаточна для большинства практических расчетов. Так, например, для массивного кругового кольца, радиус которого лишь в 5 раз превышает радиус его поперечного сечения, погрешность при расчете по принципу средних геометрических расстояний составляет около 0,2 %.

Принцип средних геометрических расстояний может быть применен к расчету индуктивностей и при весьма высокой частоте. В этом случае, сделав дополнительное предполо­жение о равномерности распределения тока по поверхности провода, можно утверждать, что собственная индуктивность контура равна взаимной индуктивности соответствующих эквидистантных нитей, отстоящих одна от другой на расстоянии, равном среднему геометрическому расстоянию не площади, а периметра поперечного сечения провода от самого себя. Допускаемая при этом погрешность - того же порядка, что и в случае низкой частоты.

Взаимная индуктивность двух эквидистантных плоских контуров с конечными размерами поперечных сечений может быть приближенно принята равной взаимной индуктивности двух соответствующих нитей, имеющих такую же форму и такие же размеры, как оси рассматриваемых контуров, и расположенных так, что кратчайшее расстояние между ними равно среднему геометрическому расстоянию площадей (или соответственно периметров) ближайших друг к другу поперечных сечений контуров.

Допускаемая при этом погрешность еще меньше, чем при определении собственных индуктивностей.

ПРИМЕР 10

Определить индуктивное и активное сопротивления электрода ДСП-50.

При расчете использовать результаты, полученные в предыдущих примерах.

Решение

Индуктивное сопротивление электрода определяем по выражению

,

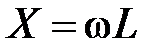где 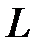– индуктивность электрода.

Индуктивность i-го электрода

.

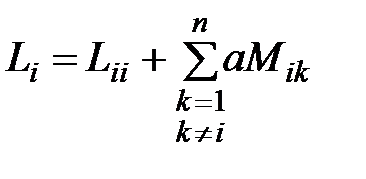где 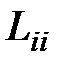– собственная индуктивность электрода,

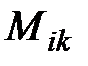– взаимная индуктивность любой пары электродов.

Коэффициент а определяется по выражению .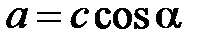

Собственная индуктивность электрода может быть определена по выражению (4.57 – 4.59).

Для проводника круглого сечения (для электрода диаметром 500 мм с учетом «обсасывания» диаметр составляет 450 мм) с. г. р. 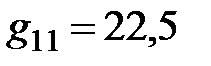см.

Расчетная длина электрода составляет 4326 мм.

Отношение .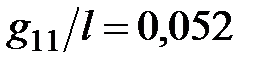

Собственная индуктивность по выражению (4.58) 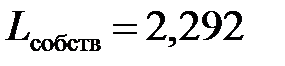мкГн, а по (4.59) 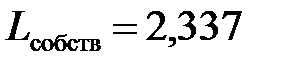мкГн.

Взаимная индуктивность может быть также определена по выражениям (4.57 – 4.59).

Среднегеометрическое расстояние площадей поперечного сечения электродов (1 и 2, 1 и 3) определяется по выражению

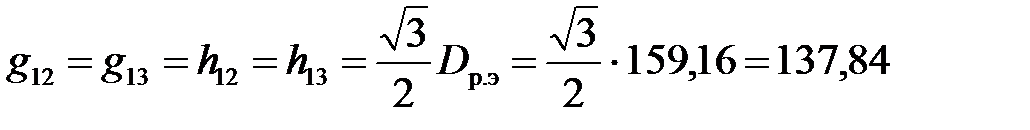см.

Взаимная индуктивность между электродами по выражению (4.58) 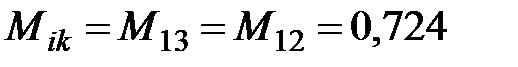мкГн, а по выражению (4.59) 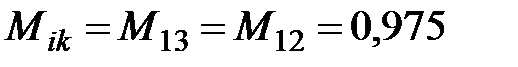мкГн.

Значения 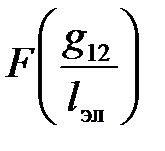и 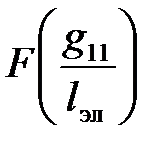приняты по [5, табл. 5.2].

Индуктивность электрода

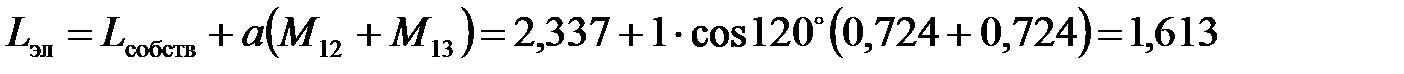мкГн.

Индуктивное сопротивление электрода

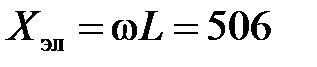мкОм.

Активное сопротивление электрода определяется по выражению

,

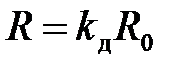где ,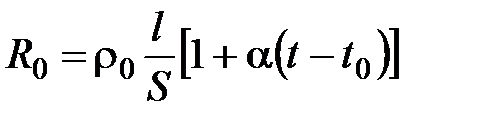

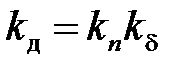– коэффициент добавочных потерь: 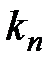- коэффициент поверхностного эффекта,

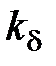– коэффициент близости.

Коэффициент поверхностного эффекта учитывает неравномерное распределение плотности переменного тока по поперечному сечению уединенного проводника (убывание плотности тока от поверхности к центру поперечного сечения). Этот коэффициент может быть определен с помощью номограмм [1, рис. 2.37].

Коэффициент близости учитывает неравномерное распределение тока по сечению проводника, вызванное наличием соседних проводников, по которым протекает переменный ток. Этот коэффициент может быть определен с помощью номограмм [1, рис. 2.38,].

Коэффициент добавочных потерь электродов может быть определен в зависимости от 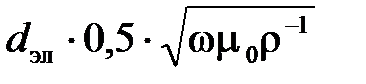для различных отношений 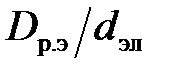по [1, рис. 2.39].

Для расчета необходимо знать отношение 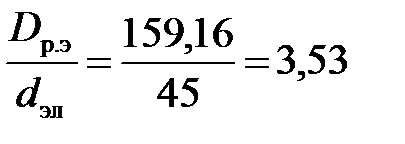и .

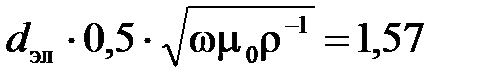Коэффициент добавочных потерь находим по [1, рис. 2.39] .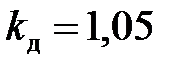

Активное сопротивление электрода 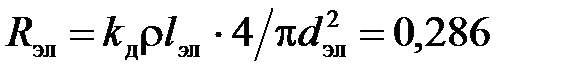мОм.