Расчет индуктивности элементов короткой сети

Реактивное сопротивление участка короткой сети оп­ределяется частотой тока и действующей индуктивно­стью ( 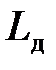). Под действующей индуктивностью следует понимать индуктивность, обусловленную общим взаимо­действием всех потоков самоиндукции и взаимоиндук­ции. Собственной индуктивностью или коэффициентом самоиндукции контура называют отношение потока са­моиндукции к силе тока в нем:

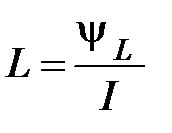. (4.44)

Взаимной индукцией или коэффициентом взаимной индукции двух цепей называется отношение полного по­тока взаимной индукции, сцепляющегося с контуром одной из цепей к силе тока в другой цепи:

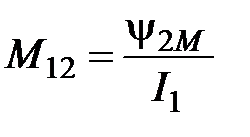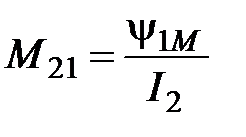, , (4.45)

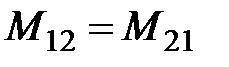(по теории взаимности).

Потоком самоиндукции контура называется полный магнитный поток, сцепляющийся с этим контуром и обусловленный током в нем, а потоком взаимной индук­ции — полный магнитный поток, сцепляющийся с дан­ным контуром и обусловленный токами в других конту­рах.

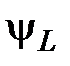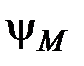Предполагается, что магнитная проницаемость сре­ды, в которой замыкаются магнитные линии потоков самоиндукции и взаимоиндукции, не зависит от величи­ны напряженности магнитного поля. При этом условии потоки и пропорциональны обусловливающим их токам, а индуктивности L и М не зависят от токов и определяются лишь формой и геометрическими разме­рами контуров, магнитной проницаемостью проводов и окружающей их среды, а при переменном токе так же и характером распределения токов по сечению проводни­ков. Взаимная индуктивность зависит еще и от взаимно­го расположения контуров. На каждом участке одно­фазной или трехфазной сети, состоящей из двух и более проводников, индуктируется не только ЭДС самоин­дукции, обусловленная переменным током в этом проводнике, но также и ЭДС взаимной индукции, обу­словленная токами в других проводниках сети. Из уравнения, определяющего энергию магнитного поля участка однофазной сети, состоящей из двух одинаковых проводников находим действующую индуктивность

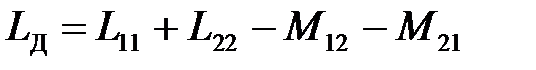, (4.46)

где 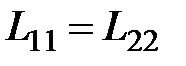– собственные индуктивности проводни­ков 1 и 2;

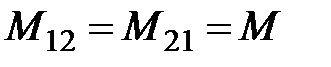— взаимные индуктивности меж­ду проводниками 1 и 2.

Действующая индуктивность i-го проводника трех­фазной или многофазной короткой сети

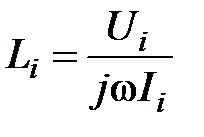, (4.47)

где 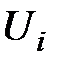– реактивное падение на i-том проводнике;

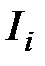– ток в нем;

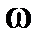– угловая частота.

Действующая индуктивность i-того проводника любой фазы может быть определена по следующей фор­муле:

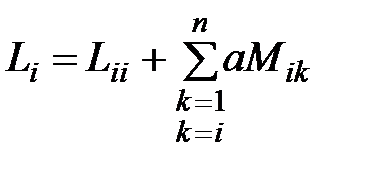, (4.48)

где 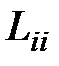– собственная индуктивность проводника;

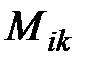– взаимная индуктивность между проводниками различ­ных фаз;

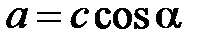– составляющая комплекса соот­ношения векторов токов, протекающих по проводникам i и к;

с – характеризуется отношением токов по величи­не модулей;

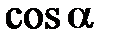– определяется сдвигом векторов то­ков по фазе.

При симметричной трехфазной системе

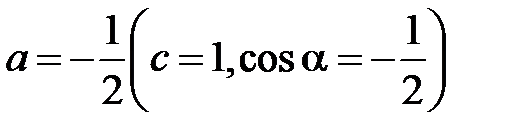. (4.49)

При определении взаимоиндукции от проводников с линейным током на проводники с фазным током 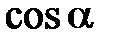будет иметь следующие значения:

а) от 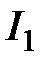на :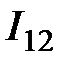

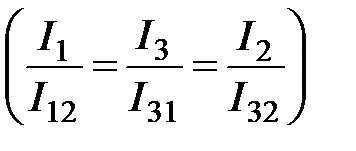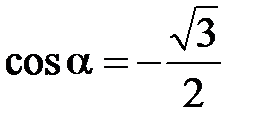, ; (4.50)

б) от 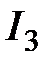на :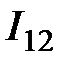

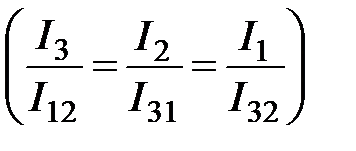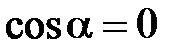, ; (4.51)

в) от 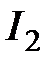на :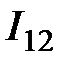

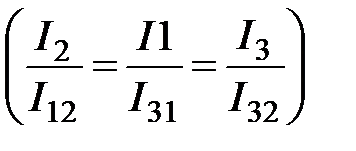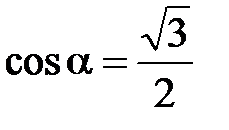, . (4.52)

При симметричной системе линейных и фазных то­ков .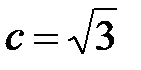

Предлагаемые ниже расчетные формулы приведены к виду, при котором значения реактивных сопротивле­ний получаются в омах (Ом), а индуктивности в генри (Г). При этом все линейные размеры в формулах сле­дует подставлять в сантиметрах (см), а при пользова­нии нормалями в метрах (м). Исходные общие выраже­ния для вывода расчетных формул принимались по ра­ботам [5].

Расчетные формулы

1. Индуктивность линейного провода в общем случае. Собственная индуктивность линейного провода в практически встречающихся случаях:

L = N — G, (4.53)

где N — величина, зависящая только от формы и раз­меров оси провода и от характера распределения тока по сечению;

G — величина, зависящая от формы и раз­меров поперечного сечения и характера распределения тока по сечению.

а). Для прямолинейного провода:

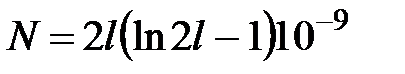, (4.54)

где — длина провода.

б). Для провода, изогнутого по дуге окружности,

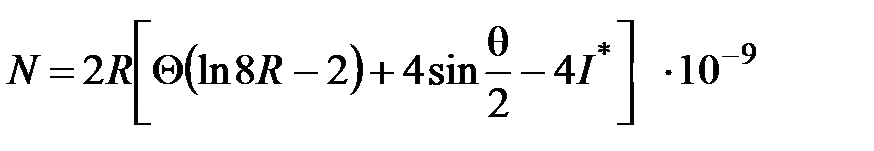, (4.55)

где R — радиус окружности, по дуге которой изогнута ось провода;

— центральный угол, соответствующий дуге провода, в радианах;

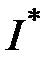— величина, значения ко­торой для различных углов приведены в [5, табл. 5.1].

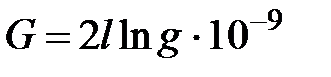, (4.56)

где g — среднее геометрическое расстояние площади поперечного сечения провода от самой себя (с. г. р.).

Собственная индуктивность проводников ( 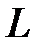)может быть определена по формуле

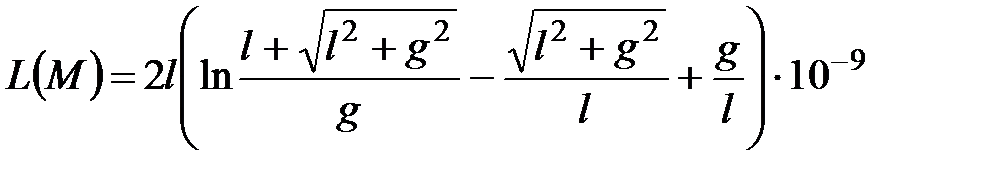. (4.57)

В случае :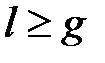

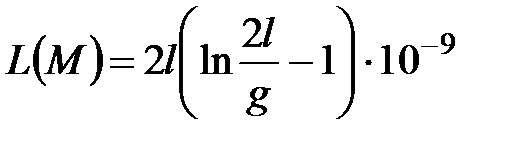. (4.58)

Для расчета собственной индуктивности удобнее пользоваться формулой

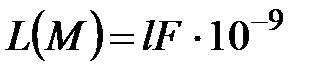, (4.59)

где 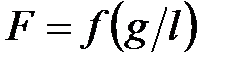— приведены в [5, табл. 5.2] для наиболее часто встречающихся отношении .

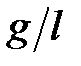Средние геометрические расстояния (с. г. р.) некото­рых проводников и фигур приведены ниже:

С. г. р. прямолинейного отрезка длиной b от самого себя

g= 0,223b. (4.60)

С. г. р. площади круга от самой себя

g= 0,779r. (4.61)

С. г. р. площади круглого кольца с внутренним и на­ружным радиусом 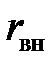и 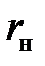от самой себя определяется формулой

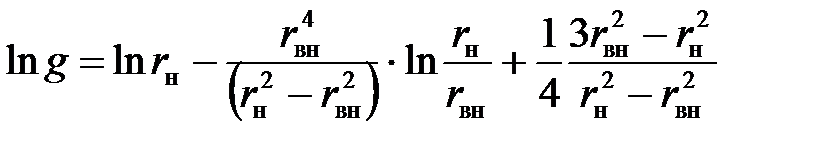(4.62)

или можно пользоваться формулой

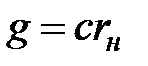, (4.63)

взяв значения коэффициента с из [5, табл. 5.3].

Для основных типоразмеров трубчатых проводников имеем:

g = 2,1945 см для 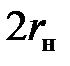= 50 мм, 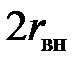= 30 мм;

g = 2,6838 см для 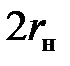= 60 мм, 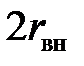= 40 мм.

Для оценки с. г. р. можно пользоваться также фор­мулой 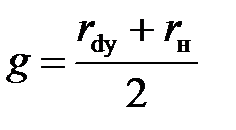, однако ее точность не превышает 10 %.

С. г. р. площади прямоугольника от самой себя со значительной степенью точности определяется форму­лой

g = 0,2236 (b + с), (4.64)

где с и b — стороны прямоугольника.