Вопрос 20. Уравнение движения АТС.
Кроме вышеназванных сил для отдельных звеньев автопоезда внешними также являются силы взаимодействия в сцепном устройстве. Для различных звеньев автопоезда эти силы имеют различное направление и величину. Для тягача Р 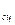 - сила сопротивления движению, для прицепа Р
- сила сопротивления движению, для прицепа Р 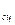 - движущая сила. Эту силу можно определить только из решения уравнения движению для каждого звена автопоезда.
- движущая сила. Эту силу можно определить только из решения уравнения движению для каждого звена автопоезда.
Напишем уравнение движения для одиночного автомобиля:
m  j
j 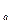 = R
= R 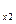 - R
- R 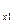 - P
- P 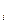 - P
- P 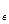 , (1.38)
, (1.38)
где: R 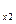 - суммарная реакция дороги на ведущих колесах:
- суммарная реакция дороги на ведущих колесах:
R 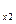 = Р
= Р 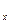 - R
- R 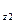 f
f 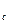 - (I
- (I 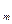 u
u 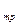
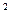
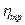 +I
+I 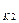 j
j 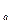 )/r
)/r 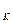 r
r 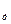 , (*)
, (*)
а R 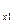 = - (R
= - (R 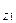 f
f 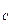 + I
+ I 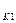 j
j 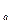 / r
/ r 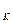 r
r 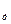 ), (**)
), (**)
Подставляем выражения (*) и (**) в (1.38), с учетом того, что Р 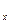 = Р
= Р 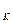 , имеем:
, имеем:
Р 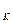 = P
= P 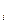 + P
+ P 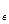 + (R
+ (R 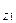 + R
+ R 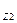 )f
)f 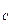 + m
+ m  j
j 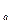
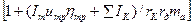 ,
,
где: R  + R
+ R  = G
= G  cos
cos 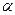 , а G
, а G 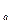 cos
cos 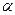 f
f 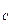 = Р
= Р 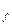 и
и 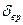 =
= 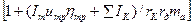 , тогда:
, тогда:
m  j
j 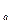
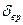 = Р
= Р 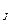 - сила сопротивления разгону (приведенная сила инерции), а
- сила сопротивления разгону (приведенная сила инерции), а 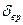 - к-т учета вращающихся масс АТС, который показывает во сколько раз сила необходимая для разгона с заданным ускорением как поступательно движущихся масс, так и вращающихся масс АТС, больше силы необходимой для разгона только поступательно движущихся масс.
- к-т учета вращающихся масс АТС, который показывает во сколько раз сила необходимая для разгона с заданным ускорением как поступательно движущихся масс, так и вращающихся масс АТС, больше силы необходимой для разгона только поступательно движущихся масс.
Удобнее считать 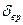 = 1 +
= 1 + 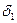 u
u 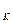
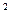 +
+ 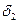 , (1.39)
, (1.39)
где: 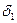 = I
= I 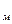 u
u 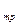
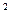
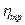 / r
/ r 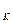 r
r 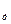 m
m  , а
, а 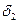 =
= 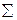
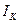 / r
/ r 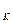 r
r 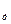 m
m 
Для одиночных автомобилей обычно 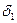 =
= 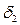 = 0,04.
= 0,04.
Таким образом, получаем выражение:
Р 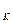 = P
= P  + P
+ P 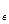 + Р
+ Р 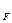 + Р
+ Р 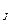 , (1.40)
, (1.40)
называемое силовым или тяговым балансом автомобиля.
Уравнение силового баланса для автопоезда:
- для тягача: Р 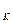 = P
= P 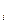 + P
+ P 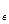 + Р
+ Р 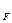 + Р
+ Р 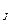 + Р
+ Р 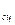 ,
,
- для прицепа: m 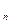 j
j 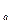 = Р
= Р 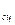 - P
- P  - P
- P 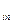 - P
- P 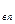 - P
- P 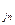 , по аналогии:
, по аналогии:
Р 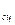 = P
= P  + P
+ P 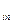 + P
+ P 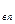 + P
+ P 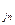 , где: P
, где: P 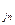 = m
= m 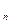 j
j 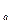
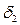 , а К
, а К 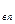 =0,25К
=0,25К 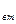 .
.
При нескольких прицепах расчет начинают с последнего, для которого Р 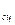 = 0.
= 0.
Мощностной баланс получаем при умножении всех сил, входящих в уравнение силового баланса на V 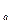 :
:
N 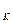 = N
= N 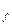 + N
+ N 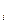 + N
+ N 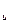 + N
+ N 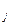 , (1.41)
, (1.41)
Дата добавления: 2021-05-28; просмотров: 630;











